
pH:水素イオン濃度の求め方(計算方法)と希釈
この記事は、「酸塩基反応と酸化還元反応の違いを答えられますか?」の続編として、
・pH(水素イオン指数)の求め方と意味、
そして入試頻出である、
・“酸or塩基をどれだけ希釈(薄める)しても、pH7(中性)を超えない理由”を解説していきます。
2019/01/14:Kw(水のイオン積)の値と温度変化について追記しました。
2018/12/4更新:続編「弱酸・弱塩基のpHの求め方と電離平衡」を作成しました!
目次(タップした所へ飛びます)
pH(水素イオン濃度)と酸/塩基の強さ
前回の内容を簡単に振り返っておくと、酸と塩基には2つの定義があり、高校化学では「ブレンステッド・ローリーの定義」を主に使用します。
これは、電離してH+(水素イオン)を放出するものを「酸」、H+を受け取るものを「塩基」として定義するものです。
これによって、アンモニアの様な水酸化物イオン(OHー)を持たない化合物も塩基であると説明できる様になりました。
詳細は>>「酸・塩基の定義と酸化還元反応」の酸塩基反応の部分を参照してください。<<
酸・塩基とpH
上記のように酸、塩基はH+のやりとりで定義されます。
そして、「強酸、弱酸、強塩基、弱塩基」と言った酸・塩基の強さは水素イオン濃度によって決まります。
つまり、H+の濃度が高いほど酸性が強く、H+の濃度が低いほど塩基性が強くなります。
その水素イオン濃度を示す指数が「pH(ピーエイチ、ペーハー:水素イオン指数)」(potential of hydrogenの略です)で、
一般に0~14の値を取り、0に近づくほど水素イオン濃度が高く酸性に、
14に近づくほど水素イオン濃度が低く(=水酸化物イオン濃度が高く)塩基性になります。
pH計算と対数について
pHの計算は、対数(常用対数)を用いて計算する為、基本的な対数の知識が必要です。
ここでは、当サイトの「常用対数」の記事から重要な部分を紹介します。詳しくは、下のリンクからご覧下さい。
$$\log _{A}B$$
の Aをその対数の底と言い、対数の底は0より大きく、かつ1でない必要があります。
またBの事を真数と言い、こちらも、Bは0より大きい条件(真数条件)があります。
\(\log _{A}B\)
上の意味は、『Aを◯乗すればBになる数』がある時、
\(◯=\log _{A}B\)
と表しているのです。
例を挙げると、A=3、B=27とするとき、$$3を\log _{3}27乗$$すれば27になる。
すなわち、\(3^{\log _{3}27}=27 と 3^{3}=27\) を比べると\(\log _{3}27=3\)
という風に表します。これが対数の基本的な考え方です。
>>詳細:「常用対数とは?その性質と応用」<<
では、実際にpHを対数を使って計算してみます。
水素イオン濃度からpHを求める方法
pHは以下の式で計算できます。
$$pH=-\log_{10}[H^{+}]・・・*$$
例えば、1(L)あたり0.01(mol)のH+が溶けている時、
$$[H^{+}]=\frac{0.01(mol)}{1(L)}=0.01(mol/L)$$
を(*)式に代入すると、
$$-\log_{10}0.01=-\log_{10}10^{-2}=2\log_{10}10=2$$
よってpH2の強酸となります。
水のイオン積Kw
もう一点、酸・塩基反応を考える際に必須の定数があり、
「水のイオン積」と呼ばれ、”Kw”であらわします。
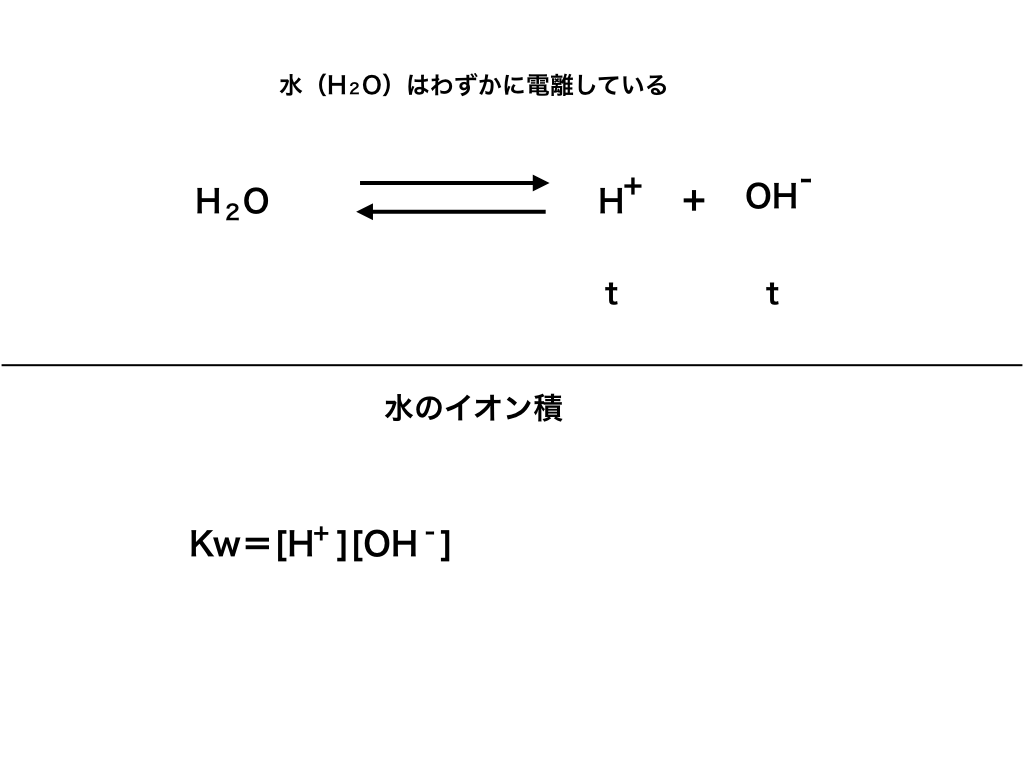
<図1>
この水のイオン積Kwは、25℃という条件のもとで、
$$Kw=[H ^{+}][OH^{-}]=1.0× 10^{-14}$$
の式が成立し、Kw=10-14の値を取ります。逆に、温度が変化すればイオン積の値も同じく変化します。
以下の解説では、温度が25℃に保たれているものとします。
酸を希釈し続けてもpHが7を超えない訳
一方で、塩酸や硝酸といった強酸であったとしても、大量の水で希釈(薄めること)をすれば、
$$水素イオン濃度{H^{+}}=\frac{水素イオンの物質量}{水溶液の体積}$$
より、分母が大きくなり、結果としてpHは中性である7に近づいていきます。
では、強酸を希釈し続けた場合、pHは7を超えるのでしょうか?
感覚的には、酸をいくら薄めてもpHが8や9と言った塩基性を示すことはあり得ないと感じるのではないでしょうか。
しかし、例えば水素イオン濃度を10のマイナス8乗(mol/L)にすれば、(*)式の計算上はpH=8と求まります。
水自体の電離が無視できなくなる
このことは、pHが7に近いときにその酸を溶かしている(溶媒である)水:H2O“自体の電離”によって説明できます。<上図1>参照
つまり、水H2Oは常にある程度電離しており、H2O⇄H++OHー の可逆反応をしています。
ただし、この電離はpHが十分に小さい(大きい)ときには“無視できる程度”なのです。
ところが、水の電離によって生じるH+は、pH6〜8の中性付近ではpHの計算におおきな影響を与えてくるのです。
硝酸を希釈して確かめる(実例)
ここでは、実際にHNO3(硝酸:電離度α=1)を薄めて行くとき、
本当にpHが7を超えないのか、計算して確かめてみます。
<図1>の様に電離します。CA(mol/L)を硝酸のモル濃度、
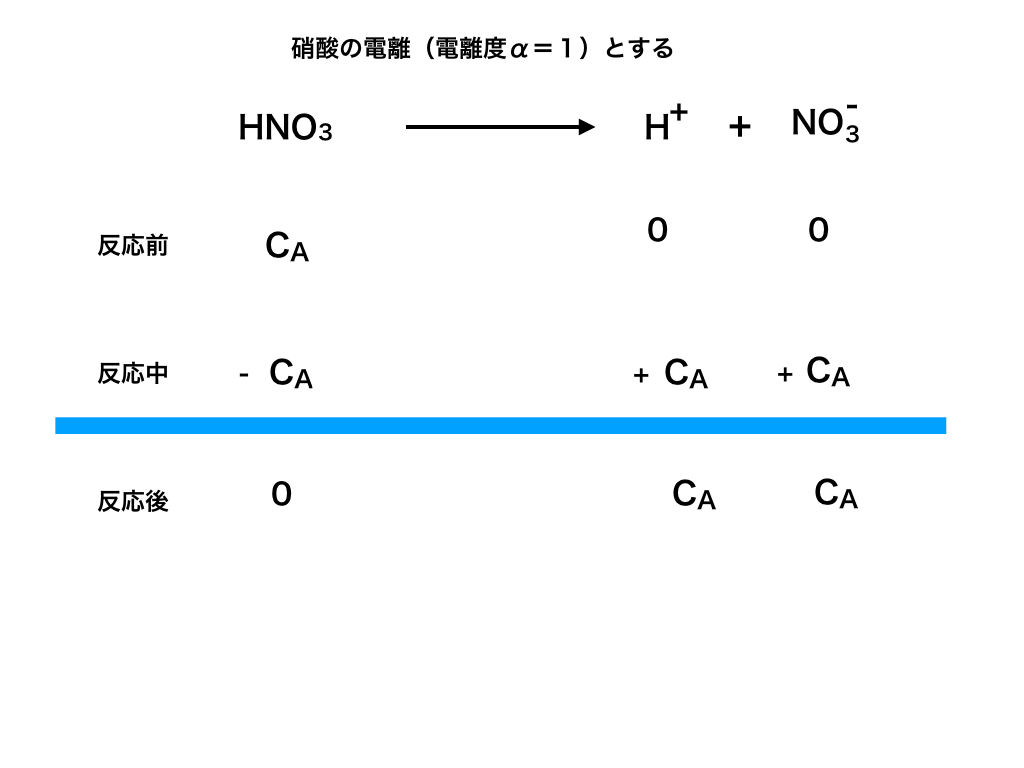
<図2>
同様に、水から電離した水素イオンと、水酸化物イオン濃度を「t」とおきます。<図1>

<図1再掲>
以上より、硝酸と水から電離した水素イオン[H+]=CA+t、水酸化物イオン[OH-]=t、
ここで、上述した水のイオン積:Kw=[H+][OH-]=1.0×10-14を利用して、
$$Kw=(C_{A}+t)(t)$$
$$t^{2}+tC_{A}-Kw=0$$
このtに関する二次方程式を解の公式を使って解くと、
t=水の電離による水素イオン濃度なので、t>0に注意して、
$$t=\frac {-C_{A}+\sqrt {(C_{A})^{2}+4K_{w}}}{2}$$
$$[H^{+}]=C_{A}+t$$より、
$$[H^{+}]=C_{A}+\frac {-C_{A}+\sqrt {(C_{A})^{2}+4K_{w}}}{2}$$
再び、(*)より、pH=ーlog10[H+]だから、
1.0×10-9(mol/L)の硝酸のpHは、
$$=-\log_{10}{\frac {C_{A}+\sqrt {( C_{A}) ^{2}+4K_{w}}}{2} }$$
この式に、\(\begin{aligned}C_{A}=1.0× 10^{-9}(mol/L) \\
K_{w}=1.0× 10^{-14}\end{aligned}\)を代入して、
$$pH=-\log_{10}{\frac {10^{-9}+\sqrt {10^{-18}+( 4× 10^{-14}) }}{2}}$$
この式を整理すると、、、
$$pH=-\log_{10}{ \frac {1+\sqrt {40001}}{2× 10^{9}}}$$
これを計算すると、(実際にはここまで複雑な問題は出ません)
pH≒6.99783 、と求まります。
このpHの値は限りなく7に近い数値ですが、7を超えて塩基性にはなっていません。
これで、どれだけ希釈しても酸が塩基性になることはないことが計算できました。
逆に塩基をどれだけ薄めても、酸性にはなりません。
*入試では、この複雑な計算の代わりに文字で証明させる問題が出ることがあります。
が、一度この手順を見れば対応できるはずです。
ちなみに、、(極限を使ってみる:上級編)
今回硝酸HNO3の濃度を1.0×10-9(mol/L)としましたが、もっと限りなく薄めてみましょう。
具体的には、$$C_{A}=1.0 \times 10^{-n} (mol/L)として、$$
$$pH=-\log_{10}{\frac {C_{A}+\sqrt {( C_{A}) ^{2}+4K_{w}}}{2} }$$
に代入し、lim(n→∞)を取ってみるのです。
$$\lim _{n\rightarrow \infty }\frac {10^{-n}+\sqrt {10^{-2n}+4\times 10^{-14}}}{2}$$
$$=\frac {\sqrt {4× 10^{-14}}}{2}=\frac {2× 10^{-7}}{2}=10^{-7}$$
pH=ーlog10[10-7]=7・log1010=7
よって、pH=7が示されました。
pHの計算(弱酸・弱塩基)と電離平衡の記事へ
次回は、弱酸(酢酸など)・弱塩基のpHの求め方を解説していきます。
関連記事
>>・「弱酸・弱塩基のpHの求め方と電離平衡をわかりやすく!」<<new!
今回のようなpHに関する問題は(特に平衡分野と融合して)頻出です。
「おすすめの化学の演習用問題集3選」で、インプットした知識を問題を解きながら定着させてみてください。
今回も最後までご覧いただき本当に有難うございました。
このサイトは皆さんの意見や、記事のリクエスト、SNSでの反応などをもとに日々改善・記事追加更新を行なっています。
そこで ・記事リクエストと質問・ご意見はコメント欄にお寄せください。可能な限り対応します。
・また、多くの学生・受験生に利用して頂くためにSNSでシェア(拡散)&当サイト公式Twitterのフォローをして頂くと助かります!
・より良いサイト運営・記事作成の為に是非ご協力お願い致します!
・その他のお問い合わせ/ご依頼等はお問い合わせページよりお願い致します。

