”状態”の変化と熱量の計算
<この記事の内容>:『物質の三態』のところで学ぶ、固体・液体・気体の”3つの状態の変化”と、
・熱量と状態変化の関係を表した図、
・さらに基本的な計算問題(比熱と蒸発/融解熱)の解き方を具体的な問題を通して紹介しています。
<関連記事>:「蒸気圧の意味と蒸気圧曲線・状態図の見方」
目次(タップした所へ飛びます)
物質の三態とは
まず物質の三態(固・液・気)の特徴と、それぞれの変化について詳しくみてみましょう。
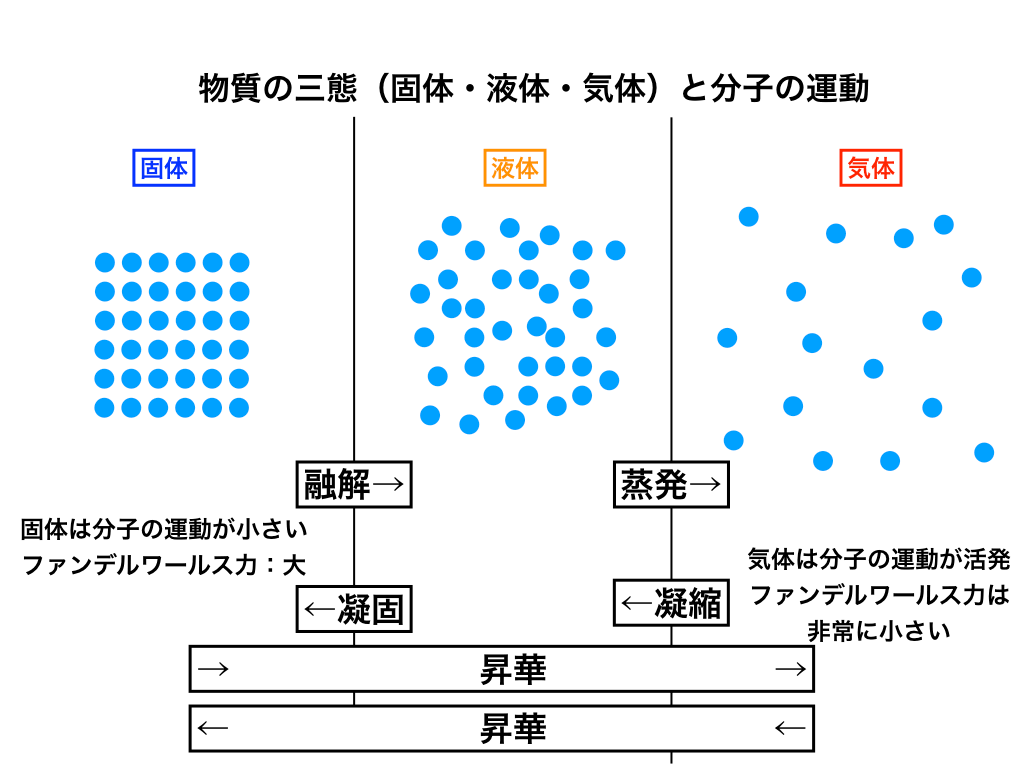
固体の特徴
上の図のように、固体は各分子がほとんど運動(熱運動)しておらず、分子間に働く引力(ファンデルワールス力)が大きいと言う特徴を持ちます。
通常の状態変化では、『融解』して液体になる、あるいは、逆に『液体』から『凝固』して固体になります。
が、注意しておくべき例外として、
・ナフタレン\(C_{10}H_{6}\),
・ヨウ素\(I_{2}\),
・二酸化炭素\(CO_{2}:ドライアイス\)
の3つは、液体を経由せずにそのまま『気体』となる、”昇華”という現象が起こります。
同様に、気体からも「昇華」して固体になる(一部の例外のみ)事もあります。
(変化の向きが逆であっても、両方ともおなじ“昇華”を使う点は要注意です)
液体の特徴
液体は、固体が『融解』、もしくは気体が『凝縮』することによってできるものです。
固体よりは各分子の熱運動が大きく、
ファンデルワールス力は固>液>気と中間で、流動性を持ちます。
気体の特徴
気体は、液体が蒸発するor【一部の固体が“昇華”する】ことで生まれる状態です。
非常に各分子の運動が激しく、ファンデルワールス力はほとんど働きません。
固体から気体への状態変化の図
ここからは、より具体的に《固体が、→液体を経て→気体へと変化する》際の『加えた熱量』と『温度の関係』を表したグラフを見ていきます。
<図1>の読み取り方
よく問題集や教科書で見かける『温度ー(加えた熱量)』の図は以下のようになっています。
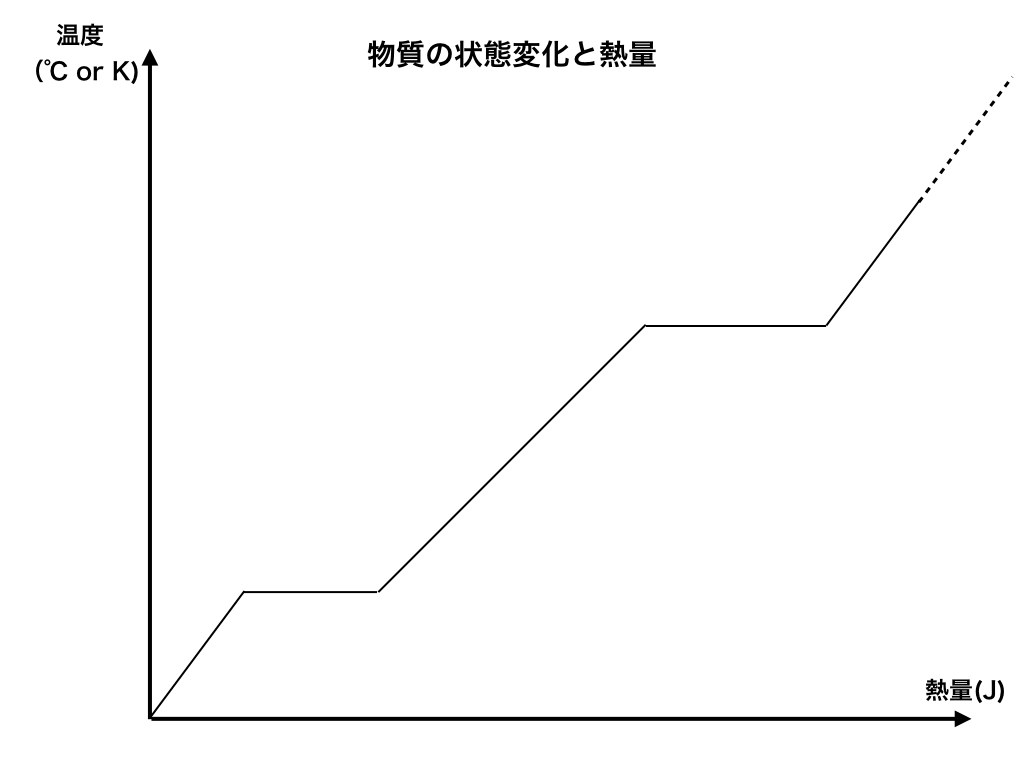
では、この図が意味する事、主に”傾いている所”と”平らなところ”について解説していきます。
いま横軸には加えた”熱量(J)”が、縦軸にはその物質の”温度(K :ケルビン or ℃)”が示されています。
図を読み取ると、熱を加えれば加えるほど温度は上昇していきます。
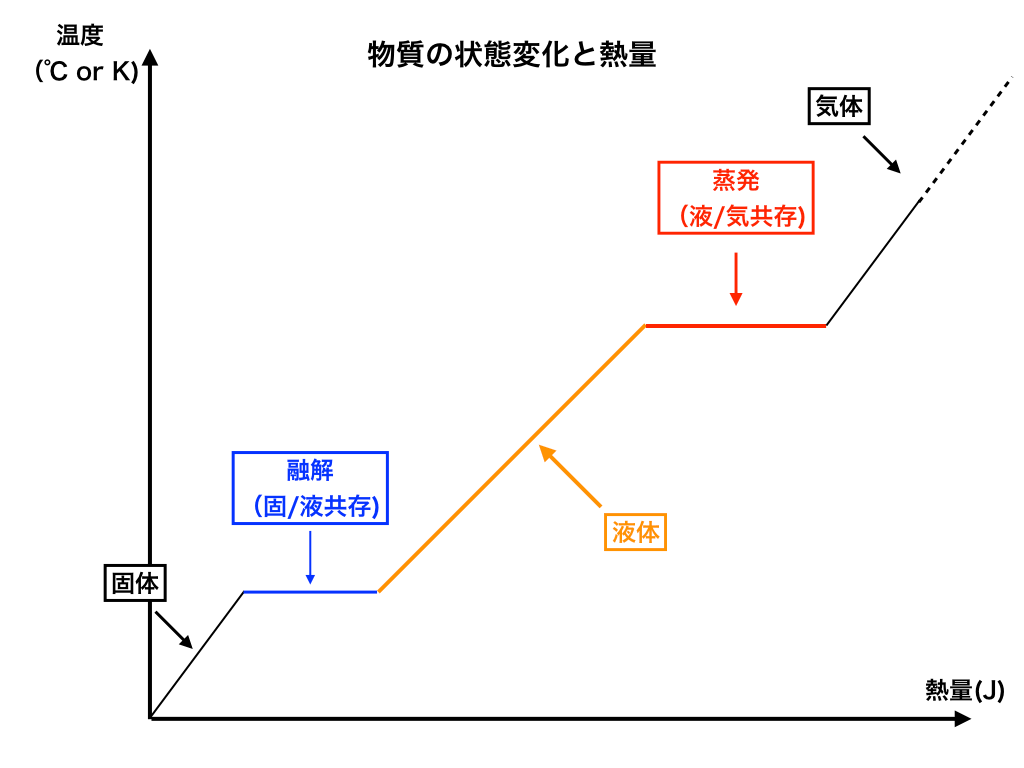
<(状態を記述した図:バージョン2)>
次にこの図2では、先ほどの線を色付けした上で、それぞれの場合の”状態”を書き加えました。
特に青色の部分と赤色の部分(”共存”と書いてある場所)は重要です。↓
【最重要事項】完全に物質が変化し切るまで温度は変化しない
熱量の計算や、<上の図ver2>の様なものを見た際に、気をつけないといけない点を紹介しておきます。
見出しの通り”全ての物質”が、ある状態から→他の状態に変化し切るまで、全体の温度が変化しないという事です。
これをもう少し分かりやすく、具体例で解説します。
いま氷が200gあり、温度が0℃であるとします。
これに熱を加えていくと、徐々に氷が溶けて水に変化していきます。
そして、50(g)が氷、150(g)が水という”固・液共存”の状態にある時、水(液)の部分だけが温度が上昇することはなく、”氷(固)”が”完全に溶けきる”まで”温度は0℃のまま”である、という意味です。
その後、200(g)全てが溶け、水になって初めて温度が上昇を始めます。
※:これは固→液の場合だけでなく、蒸発時(液→気)の場合も同様です。
(全て気体に変化するまで、温度変化が起こることはありません。)
熱量の計算
次の項で具体的な熱量の計算問題に入ります。
その前に、知っておく必要がある【熱・比熱】と、それぞれの単位についてさらっと触れておきます。
融解熱とその単位とは?
「融解熱」はその名の通り『固体の物質が液体に変化するときに必要な熱』を意味し、単位は(kJ/mol)を主に使います。
蒸発熱と単位とは?
蒸発熱も同様です。『液体が気体に変化するときに必要な熱量』で、この単位も基本的に(kJ/mol)です。
比熱とその単位
比熱は、ある物質1(g)を1度(℃、もしくは、K:ケルビン)上げる際に必要な熱量のことで、単位は\(J/K\cdot g\)もしくは\(J/℃\cdot g\)となります。
”鉄板”と”発泡スチロール”に同じ熱量を加えても温まりやすさが全く違うように、比熱は物質によって様々な値を取ります。
確認問題で計算をマスター
ここでは、熱量の計算の中でも最頻出の”水\(H_{2}O\)”について扱います。
<問題>:いま、-30℃の氷が360(g)ある。
この氷を全て100℃の水蒸気にするために必要な熱量は何kJか?
ただし、氷の比熱は2.1(J/g・K)、水の比熱は4.2(J/g・K)、氷の融解熱は6.0(kJ/mol)、水の蒸発熱を44(kJ/mol)であるものとする。
解答・解説
次の5ステップの計算で求めることが出来ます。
もう一度先ほどの図(ver2)を掲載しておくので、これを参考にしながら”今どの場所に物質(ここでは\(H_{2}O\))があるのか?”に注意して解いていきましょう。

固体(氷)の温度を融点まで上昇させるための熱量<step1>
まず、固体:-30度(氷)を0度の固体(氷)にあげるために必要な熱量を計算します。
K:ケルビン(絶対温度) でも、 摂氏(℃)であっても『上昇する温度』は変わらないので
\(2.1(J/g\cdot K)\times 30(K) \times 360(g)=22680(J)\)
【単位に注意】すべての固体を液体にする為の熱量<step2>
全ての氷が0度になれば、次は融解熱を計算します。
(※)融解熱と後で計算する蒸発熱は、単位が\(\frac{kJ}{mol}\)「1mol(=\(6.02\times 10^{23}\)コ)あたりの(キロ)ジュール」なので、一旦水の分子量\(18\frac{g}{mol}\)で割って物質量を求める必要があります。
$$\frac{質量(g)}{分子量(g/mol)}=物質量(mol)$$
したがって、\(\frac{360(g)}{18(g/mol)}=20(mol)\)
\(20(mol)\times 6(kJ/mol)= 120(kJ)\)
液体を0度から沸点まで上げるための熱量<step3>
これは、比熱×質量×(沸点:100℃-0℃)を計算すればよく、
\(4.2\times 100\times 360=151200(J)\)
液体を気体にするための熱量<step4>
先ほどの融解の場合と同様に、1mol当たりで計算するので、
\(20(mol)\times 44(kJ/mol)= 880(kJ)\)
<step5>:全てを足し合わせる
最後に、step5でこれまでの熱量(step1〜step4)の総和を計算します。
\(キロ=10^{3}\)に注意して、
$$\frac{22680}{10^{3}}+120+\frac{151200}{10^{3}}+880=$$
\(22.68+120+151.2+880=1173.88\)
有効数字2ケタで、\(1.1\times 10^{3}(kJ)\)・・・(答)
※:ちなみに、問題が続いて【100℃を超えてさらに高温の水蒸気にするための熱量】を問われたら、step5で水蒸気の比熱を計算し、step6で総和を計算することになります。
まとめと関連記事へ
・物理での『熱力学』でも、”比熱や熱容量の計算”の単元でよく出題されます。物理・化学選択の人は、頭の片隅に置いておきましょう。
蒸気圧曲線・状態図へ
"物質の状態"と"気体の問題"は関連が強く、かつ苦手な人が多い所なので「蒸気圧の意味と蒸気圧曲線・状態図の見方」は要チェックです。
また、熱化学でも扱うので「熱化学方程式シリーズまとめ」も合わせてご覧ください。
今回も最後までご覧いただき、有難うございました。
「スマナビング!」では、読者の皆さんのご意見や、記事のリクエストの募集を行なっています。
・ご意見がございましたら、ぜひコメント欄までお寄せください。
お役に立ちましたら、B!やSNSでシェアをしていただけると、とても励みになります。
・そのほかのお問い合わせ/ご依頼に付きましては、ページ上部の『運営元ページ』からご連絡下さい。

