
積分法と面積をはさみうちで示す
数学Ⅲの範囲も極限→微分→積分と進んでくると、積分法で面積や体積、グラフの線の長さと言った様々な値を求めるようになって来ます。
今回は「はさみうちの原理」を利用して「積分によって面積が求まる理由」を解説していきます。
目次(タップした所へ飛びます)
積分と面積を極限が結ぶ
・はさみうちの原理の振り返り
・y=f(x)のグラフとその面積S(x)
・任意の点tとh離れた(h>0)点
・二点での長方形とS(x)[図解]
・はさみうちと微分の定義
・積分定数
・まとめ
はさみうちの原理
今回の内容を理解するのには、はさみうちの原理(極限分野)の理解が必要なので、曖昧な人は先に→「はさみうちの原理」と「追い出しの原理」の解説 を読んでおいて頂くとよいです。
簡単に振り返っておくと、関数/数列が3つあり、
$$f\left( x\right) \leq g\left( x\right) \leq h\left( x\right)の関係である時に $$
$$\lim _{x\rightarrow \alpha }f\left( x\right) =\lim _{x\rightarrow \alpha }h\left( x\right) =\beta $$
$$f(x)とh(x)のxがx→αに近づく時に$$
$$f(α)とh(α)がβに成るのならば$$
$$\lim _{x\rightarrow \alpha }g\left( x\right) =\beta $$
$$その間に「はさまれている」g(x)も$$
$$又x→αでg(α)→βとなる。$$
というものです。
y=f(x)のグラフとその面積S(x)
ここからは図解入りで進めます。
今<図1>の様なy=f(x)のグラフがあり、その面積はS(x)で表せるとします。
<図1>の様にx=αからx=tまでの面積をS(t)として、その右端のx=tからhだけx軸正方向に動かした面積の増加分、
つまりf(x)とx軸の間でxの範囲(t+h)からtまでの面積を求めます。
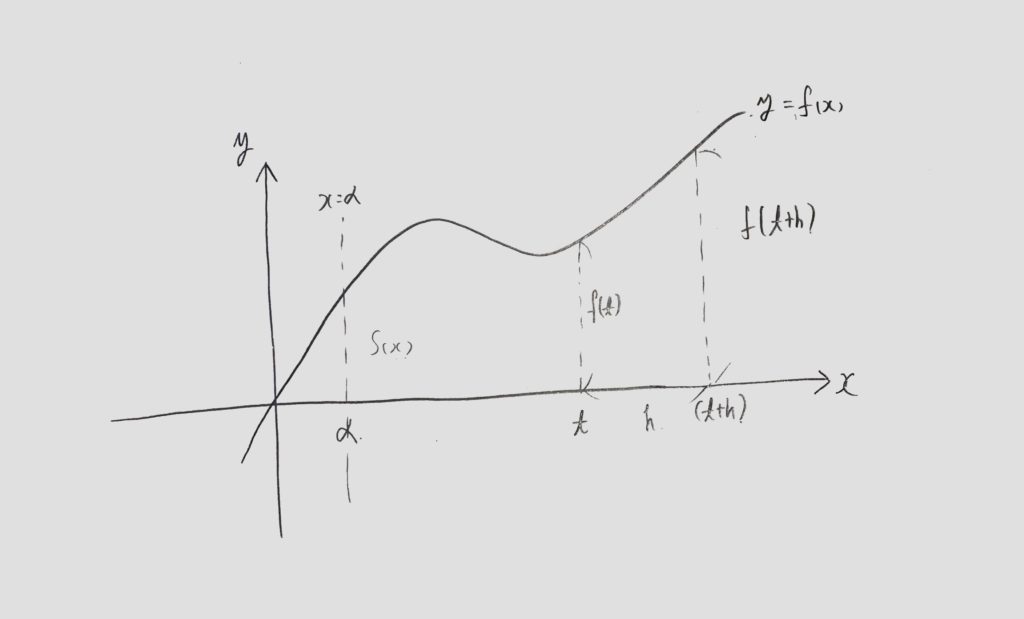
<図1>
任意の点tとhだけ離れた点(t+h):(h>0)
ここで、<図1>中の「x=tからx=t +hまで」の面積を求めたい時、その面積はS(t+h)-S(t)で計算出来ます。<図2>ー<図3>
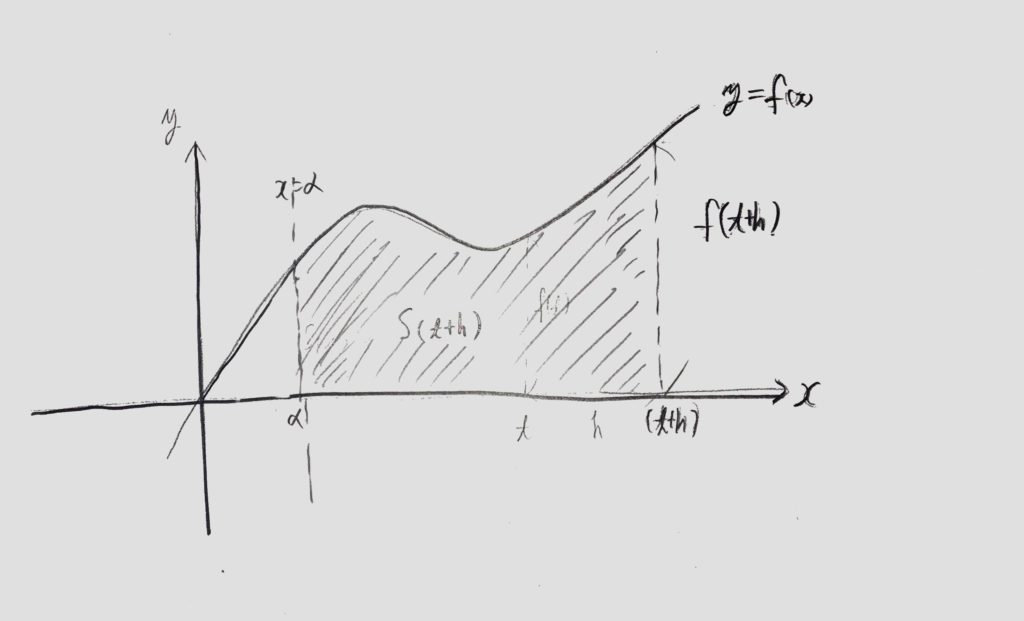
<図2>
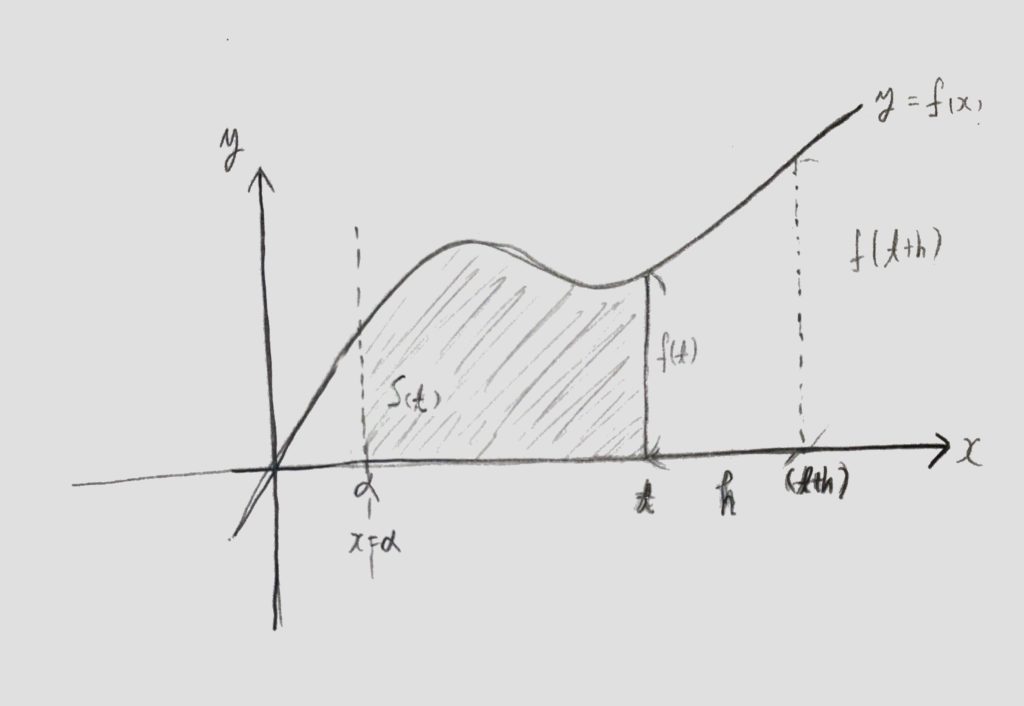
<図3>
二点での長方形とS(t+h)-S(t)
そして、今度は<図4>の部分に注目します。
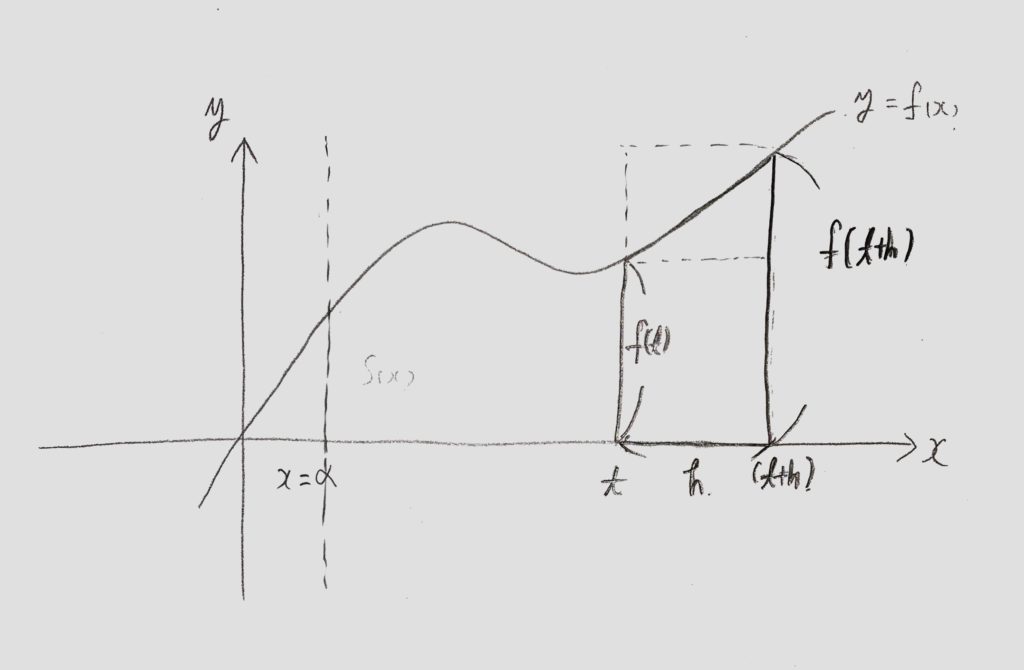
<図4>
丁度求めたい部分の面積は、
$$f\left( t\right) \cdot hの面積以上f\left( t+h\right) \cdot hの$$
面積以下である事が図からわかります。
$$ これと先ほどのS\left( t+h\right) -S\left( t\right) を考慮すると、$$
はさみうちの原理と微分の定義を使う
以下の不等式で求める面積を挟む事ができます。
$$f\left( t\right) \cdot h\leq S\left( t+h\right) -S\left( t\right) \leq f\left( t+h\right) \cdot h$$
ここで、h>0より不等式からhを割ると、
$$\frac {f\left( t\right) \cdot h}{h}\leq \frac {S\left( t+h\right) -S\left( t\right) }{h}\leq \frac {f\left( t+h\right) \cdot h}{h}$$
f(t)≦S(t+h)-S(t)/h≦f(t+h)となり、limh→0の極限を取ると、微分の定義から
$$\lim _{h\rightarrow 0}\frac {f\left( t+h\right) -f\left( t\right) }{h}=f'\left( t\right) $$
中項は=S‘(t)
$$\lim _{h\rightarrow 0}f\left( t+h\right) =\lim _{h\rightarrow 0}f\left( t\right) =f\left( t\right) $$
左辺は、=f(t)
右辺は、=f(t) となるので、
$$よって、はさみうちの原理より、S'\left( t\right) =f\left( t\right) が示せます。$$
$$(面積の微分がグラフの式と一致しました!)$$
更に、両辺を積分してみます。
∮S’(t)dt=∮f(t)dt
$$⇔S\left( t\right) =F\left( t\right) +C (Cは積分定数)・・・*$$
ここでt=αを入れてみると、S(α)=F(α) +C
S(α)は、αからα迄の面積なので、値は当然ゼロになります。
これより、0=F(α) +C ⇔C=ーF(α)
Cも求まったので、βからα迄の面積をこれまでの様に
S(β)とすると、*の式より、
$$S\left( \beta \right) =F\left( \beta \right) -F\left( \alpha \right) $$
αからβの面積は、グラフの式f(x)の不定積分F(x)のxに
βを代入したものから、αを代入したものを引いた値となり、
$$これまで使ってきた\int ^{\beta }_{\alpha }f\left( x\right) dxが$$
$$面積を表す事が示せました!$$
まとめと関連記事
この様に、「極限」を考える事で、微分と積分が結び付きました。
また、今回図形の面積をはさみうちの原理を使って評価しましたが、この方法も今後頻出するので、是非頭に入れておいて下さい。
>>「数学3の微分法・積分法とその応用まとめページ」<<
今回もご覧いただき有難うございました。
お役に立ちましたら、シェア&当サイト公式Twitter(@linkyjuku_tweet)のフォローをお願いします!
質問・記事について・誤植・その他のお問い合わせはコメント欄までお願い致します!

