
弧度法と度数法の違いと定義
<この記事を読むべき人>:「弧度法やラジアン」の意味が良く分からない人〜意味は理解できているつもりでも、「sin1,sin2,sin3 の大小関係を示せ(sin1°ではありません)」といった問題で悩んでしまう人。
目次(タップした所へ飛びます)
弧度法とは何か
高校1年で学んだ『三角比』から高校2年で学ぶ三角関数へと進むと、突然π(ラジアン)なるものが姿を現します。
この「ラジアン:π」がよく分からず、三角関数の序盤でつまずいたり、理解が曖昧なままスルーしてしまっている人も多いです。
今回はしっかり『弧度法』をマスターする事で、三角関数の”基本”を理解できるようになりましょう。
180°=π(rad)と機械的に覚えていると以下の様な初歩的な問題にすら対応できません。
(問)cos1、cos2、cos3 を大きい順に並べよ。(この問題は後で解説します。)
弧度法の定義
定義は、以下の通りです。
(例)半径1の単位円で考えると、弧の長さ(以下の図で青色のℓで塗っている部分)が「1」となる時の角度を弧度法では1(rad:ラジアン)と定義しているのです。
「弧」長と半径で定義された角「度」:を「弧度」、そしてその『法』則を「弧度法」と言います。
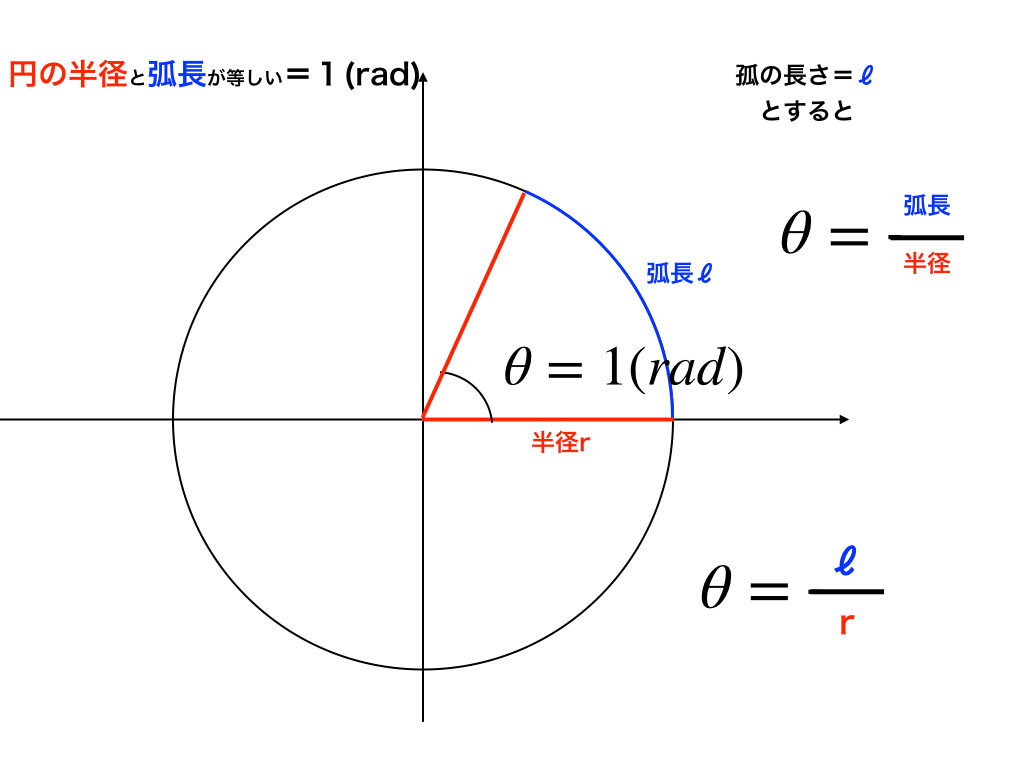
<図1:1ラジアンの解説>
2π(ラジアン)が360°である理由
では、弧度法を初めて学ぶ人が一度は疑問に思う?『2π=360°』の理由を解説していきます。
ここでも、単位円を使います。
上の図1の通り、$$θ(rad)=\frac{ℓ}{r}=\frac{弧長}{半径}$$で求まるので、今度は弧長の孤を円周全てにしてみましょう。(図2の青色で塗った部分)
こうすると、もはや”弧”という感じはありませんが、とにかく弧長=円周=2×π(ここでのπは円周率)×r(半径)であることがわかります。
そして、半径が1であることから、弧長=2πと計算できました。
ここで$$θ(rad)=\frac{ℓ}{r}=\frac{弧長}{半径}$$を思い出してみると、rが1、ℓが2πであることから、それぞれ代入するとθ=2π(rad)であることが導けます。
ここで、図2における青色で示した弧長(円周)の中心角は当然360°(度数法)です。
つまり、2π(rad)と360°が等しいことがわかりました。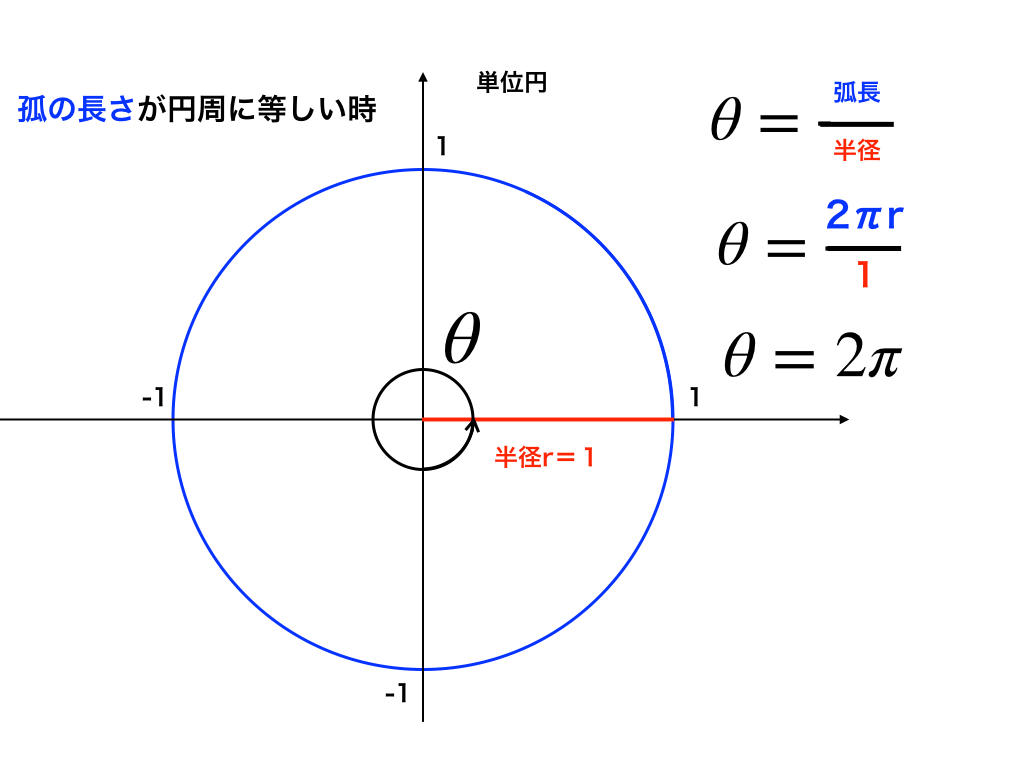
<図2>
度数法と弧度法の対応
ここまで理解してしまえば、半円の弧長がπで円周角が180°であるように、どんな角度でも弧度法を使って表すことが可能になります。
(例)45°を弧度法で表せ。
180°で割っても良いですが、より丁寧に比を使って考えてみると
45°:180°=x(rad):π(rad) ⇔180°・x=45°・π(内項の積は外項の積)
ゆえに、$$x=\frac{45°}{180°} \cdot \pi=\frac{1}{4}\pi$$と求まりました。
sin1とsin1°の違い【重要】
さて、ここまでで弧度法に関しての計算で困ることは無いはずです。
あとは冒頭でお話しした「sin1,sin2,sin3の大小関係を調べよ」という問題を少し考えてみてください。・・・
sin1、sin2、sin3の問題の解答
ここからは、問題の解説をしながら、弧度法をもう少し深く考えてみましょう。
問題は、sin1,sin2,sin3の大小関係を調べることでした。
この問が、『sin1°、sin2°、sin3°』であればsinは単位円上で「高さ=y」を表すので、
sin1°<sin2°<sin3°であることが簡単にわかります。
では、sin1 ならばどうでしょうか。
これはsin1(ラジアン)を意味します。
つまり、半径と弧長が同じ場所(初めの定義より)であることから、下の<図3>のx軸と赤色の線で挟んだ角度となり、度数法で表すとおよそ57°となります。
そして、sin180°=sinπ のπは円周率3.1415...なので180°が3.14に対応することを利用します。
するとsin2、sin3も同じく、sin114°、sin171°(いずれも”およそ”です)であることがわかります。
あとは、これを単位円上の高さ(x軸に平行に線を引く)を比べれば、
・青の点線で表したsin2が最も大きく、
・次に赤の点線のsin1、
・最も小さいものが紫の点線のsin3であることがわかります。
ゆえに、\(\sin 2>\sin 1 >\sin 3 ・・・(答)\)
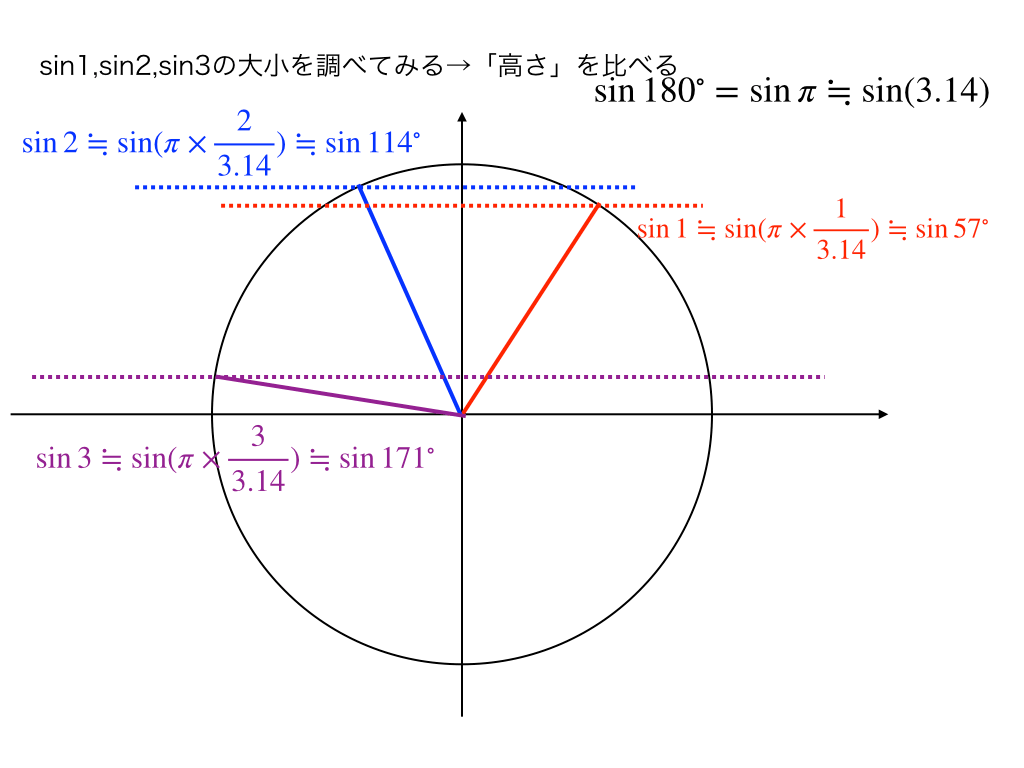
<図3>
弧度法まとめと極限・三角関数の微分積分
・ここまで読んできて、『なぜ”わざわざ”弧度法を用いる必要があるのか』疑問に思う方がいるかもしれません。
実は、弧度法の便利さが一番わかるのは、三角関数の極限や微分・積分を扱うときなのです。
・しかし、数2Bまでしか習わない人にとっても、『弧度法』を本質的に理解しておく事によって、少しひねった(先ほどの大小関係のような問題)でも、焦らず確実に得点源にする事ができます。
・基本的な事ですが、あいまいにせずしっかりと復習して理解できるようにしておきましょう。
三角関数の公式『第二の関門』攻略記事・関連記事一覧へ
三角関数では、三角比と比べてもかなりたくさんの公式を扱う事になります。
この『公式をどのようにして身に付けるのか』が、三角関数第二の関門です。
しかし、ここまで読んでくださった方なら「【丸暗記厳禁】三角関数の公式は加法定理から覚えず導く!」←こちらの記事を上から順に読んでいく事で、細かいものを入れると30を超える公式も、ほとんど覚えずに済むようになります。【要チェック&ブックマーク推奨です!】
今回も最後までご覧頂き、有難うございました。
当サイト「スマナビング!」では、読者の皆さんのご意見・ご感想や、記事リクエストの募集をコメント欄にて行なっています。
また、お役に立ちましたら いいね!、B!やシェア、Twitterのフォローをしていただけると励みになります。
・その他のお問い合わせ/ご依頼につきましては、お問い合わせページからご連絡下さい。

