
光波の干渉が苦手な人へ!
高校物理で苦手な範囲を聞くと「波動」、その中でも「光波の干渉(実験)」と答える人がかなり多いです。
恐らくその原因は、
(一)何をやっているのかイマイチ理解できていない(見通しが立っていない)こと。
(二)これからお伝えする重要なたった2つのことに注目出来ていないからです。
また、干渉実験と言っても何種類もあります。
(ヤングの二重スリット実験・薄膜干渉・くさび形空気層・回折格子・ニュートンリング・・・)
これらを全て別々に捉えていませんか?
基本的には道具が変わっているだけで全て同じ考えで解けるのです。早速詳しく解説して行きます!
(第二回:ニュートンリングと回折格子を作成しました。この記事を読み終わってから是非ご覧ください。)
目次(タップした所へ飛びます)
干渉実験で重要なのは「位相」と「光路差」2つだけ
色々な実験で色々なことを聞かれますが、結局のところ
・「位相=タイミングのズレ」と
・「光路差=経路差の光波バージョン」
の二つを抑えれば、全て同じことを言っていることがわかります。
干渉とは?
そもそも干渉とは、いくつか(複数)の波が重なる(重ね合わせ)ことで新しい波形ができる事を言います。
特に光波の干渉実験(の問題)では、基本的に波長λ(m)と振幅A(m)が同じ2つの波に注目していきます。
そして、波の山と山が重なった時に、振幅が最大=光波ならば明るくなる、山と谷が重なると振幅0=暗くなります。
「位相」とは何か?
位相というと難しそうですが、要するにタイミングの事で、下の図1(薄膜干渉実験)を見てもらいながら解説しておきます。
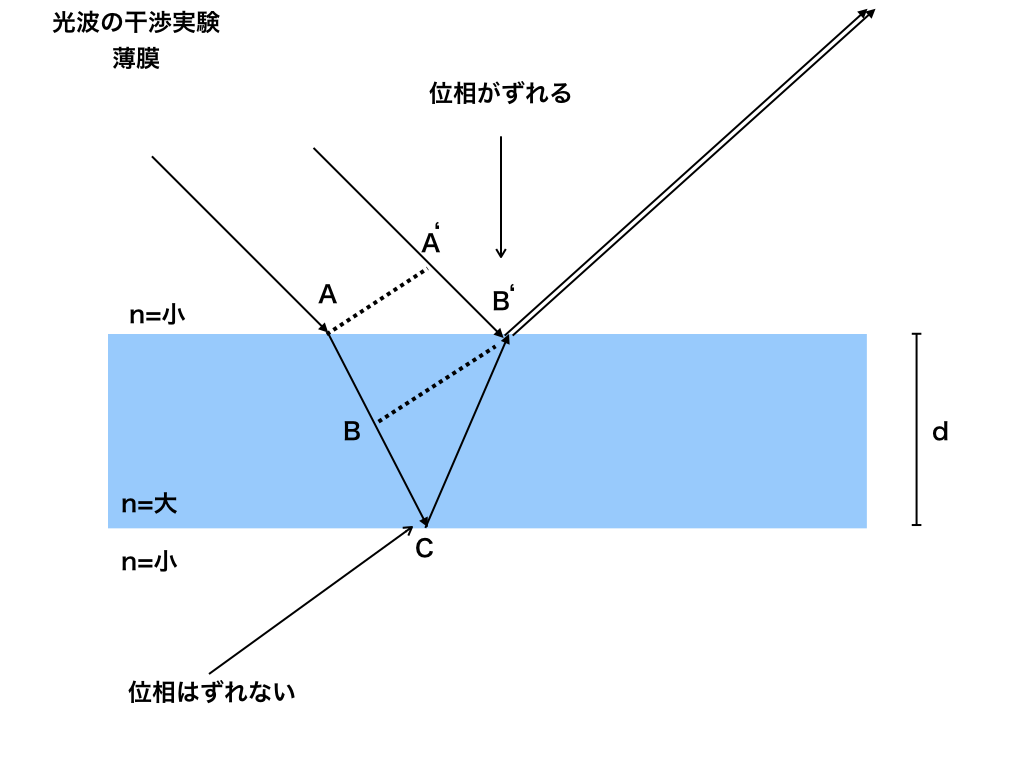
<図1>
光が進みやすいところ(n:屈折率が小さいところ)から、光が進みにくいところ(屈折率が大きいところ)で反射すれば位相がπズレて、波が逆転する。(固定端反射と基本的に同じイメージです。)
光が進みにくいところから、光の進みやすいところで反射すれば位相はズレない。(これは自由端反射のイメージ)
のちに紹介するヤングの二重スリット実験では、位相をそろえる工夫がされています。
「光路差」とは何か?
光が進む「距離」の差のこと。
考え方は基本的に「行路差」と同じですが、屈折率などによって違いが出るので「光路差」と呼びます。
位相と光路差を組み合わせて波長と比べる
上の2つを組み合わせて、波長λ(m)と比べる事で大抵の場合は解くことができます。具体的に説明していきます。
⒈光路差(光の進んだ距離、光の行路差)が
$$波長λのm倍か、\left( m\pm \frac {1}{2}\right) \lambda 倍か$$(mを整数とする)
2、波の位相は揃っているか、πズレているか
整理すると
1:光路差(行路差)が波長の整数倍(mλ)で位相が揃っていれば、2つの波は重なり合う為、明るくなる。
2:光路差が波長λの$$\left( m\pm \frac {1}{2}\right)倍$$
で位相が揃っていれば、山と谷が干渉して暗くなる。
3:位相がπずれている時は、光路差が$$\left( m\pm \frac {1}{2}\right) \lambda $$
ならば波が重なり明るくなる、
4:位相がπずれていて、光路差が波長λの整数倍mλであれば、波が打ち消しあい暗くなる。
この組み合わせが全てです。これを具体的に薄膜干渉実験で見て行きます。
薄膜干渉実験で干渉の基礎を学ぶ
薄膜の干渉実験では、<図2>のように、薄膜の上部B'で反射された光と薄膜の内部下Cで反射された光がどのように干渉するかを調べます。
上の項でも述べましたが、「位相」と「光路差」のチェックが全てなので、確認して行くと、
・B’で反射された光は屈折率大ではね返されているので位相がπずれ、
・Cで反射された光は屈折率小で跳ね返されているので位相はずれません。
次に確認するのは「光路差」でした。
今2つの光の進んだ距離の差(光路差)は太線部分のBCB’の長さになります。
ですが、Cで反射する光はBCB'の距離(行路差)よりも長い距離を進んでいます。
これは、屈折率nが大きいところを通っているので光波は進みづらいためです。
幾何的な距離(行路差)に屈折率nを掛けたものが光路差となります。
これをうまく計算できるようにしたのが<図3>です。

<図2>
<図3>(下図)では、CB'を折り返すことで、光路差をBB''の直線の長さを求めれば良いように工夫しました。
今、薄膜の厚さはdとわかっているので、三角形BB'B''に注目すると、その光路差は
\(2d \cosθ \times n \)と求まります。
あとは、光波の波長と比べて何倍かを計算する+位相が揃っていないことに注意して計算して行きます。
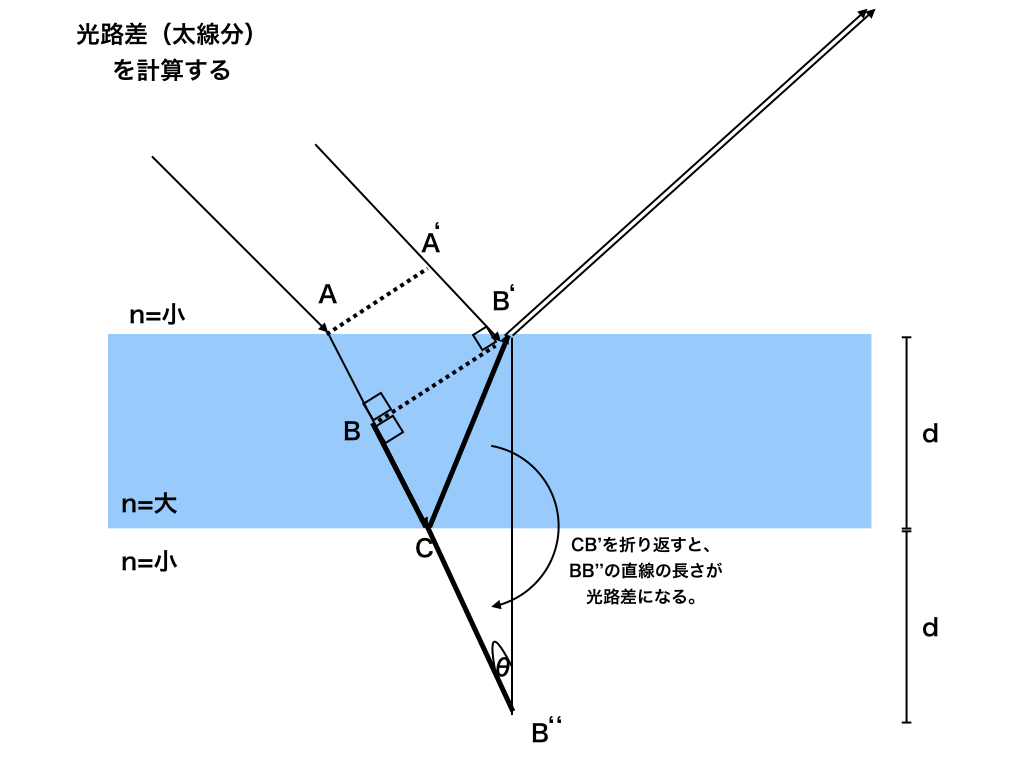
<図3>
$$すなわち、2nd\cos \theta =m\lambda ならば$$
位相がズレているので暗くなります。ゆえに、この薄膜での干渉によって明るく見える為には、
$$2nd\cos \theta =\left( m+\frac {1}{2}\right) \lambda $$
である必要があります。
少し干渉実験のことが分かってきたでしょうか?
どの干渉実験でも基本の考え方は同じ、ということを示すために次はくさび形空気層の実験を見て見ましょう。
くさび形空気層実験で確認してみる
くさび形空気層実験とは、<図4>のように2枚のガラス板なす角をθとなるように右側にものを挟んで真上から光をあてることで干渉を見るものです。
この図はわかりやすくするためにかなり誇張して描いており、実際には右側のはさむものは薄い紙一枚程度です。
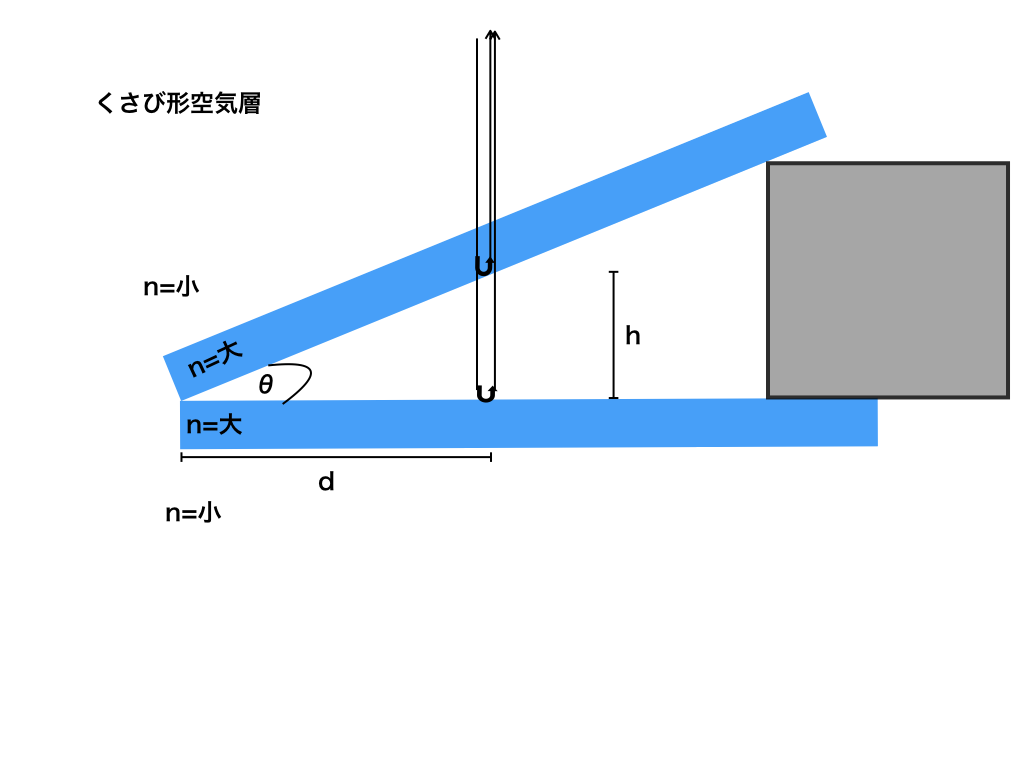
<図4>
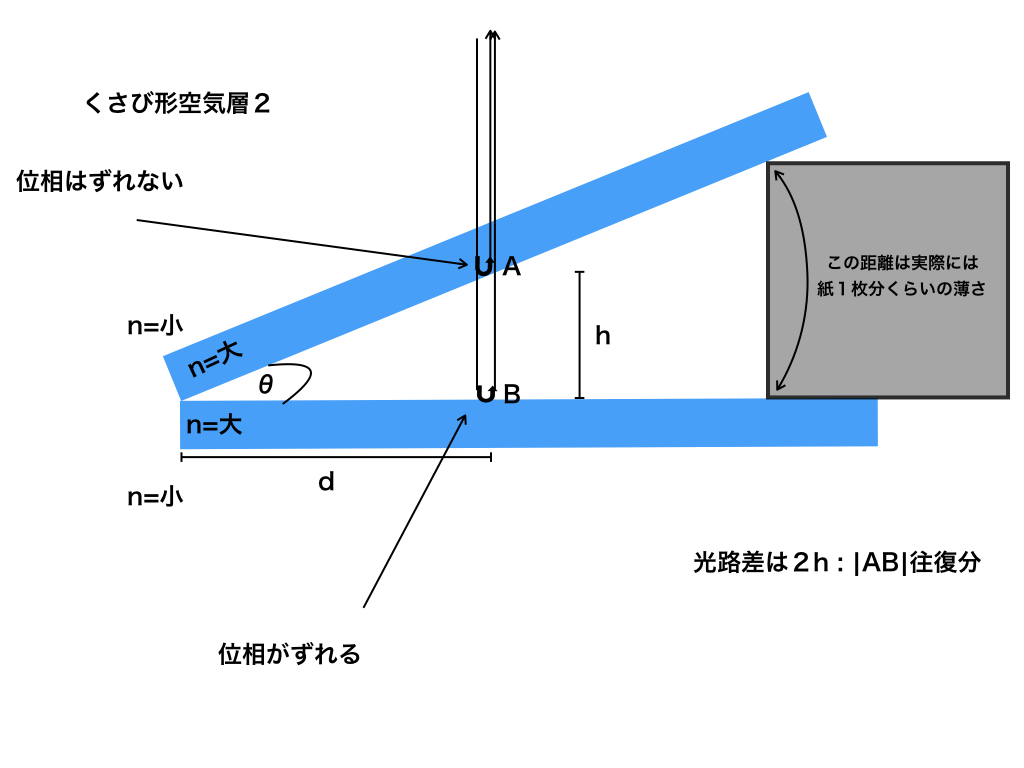
<図5>
くさび形空気層の問題でもする事は同じです。
まず位相のズレは、Aで反射した光波は屈折率大→屈折率小(空気層)で反射しているのでズレなし。
Bで反射した光波は屈折率小→屈折率大で反射しているのでズレはπ。
次に光路差の計算をすると
$$h\times 2 (AB間の往復距離)=2h $$
となります。
従って、この干渉した光を真上から見た時明るく見える条件はmを整数として
$$(\left( m+\frac {1}{2}\right) \lambda =2h)$$
となります。
ヤングの二重スリット実験
次はヤングの二重スリット実験を見てみましょう。<図6>
この実験では「光源からの光波の位相や波長をそろえる工夫」がなされています。
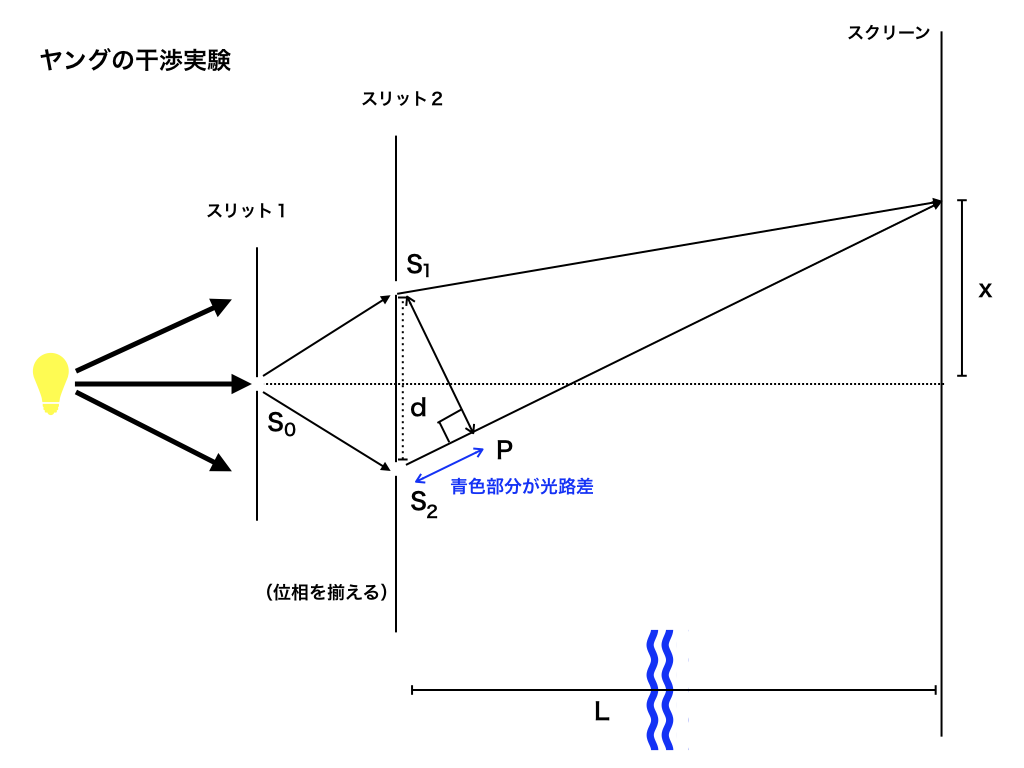 <図6>
<図6>
二重スリットを使って同位相にする工夫
普通は、上の薄膜干渉実験の様に位相をチェックしなければいけないのですが、ヤングの二重スリット実験ではその必要が無い様に工夫されています。
位相をそろえる理由と方法
この工夫の理由と方法は、記述問題などで問われることがあるのでしっかりと理解しておきましょう。
ヤングの二重スリット実験では、位相を同じにする為に光源に近い板にスリット一つ、スクリーンに近い板にスリット2つをあけて置きます。
これは、光源が様々な位相や波長の光波を出しているので、単スリット板と二重スリット板を置いて、等距離進行させると二重スリットからは同位相の光波に揃えることができるからです。(*補足1)
この様にして、スリット板を二枚置くことで位相の問題は解決されました。
従って我々は、光路差が波長の整数倍か否かを調べれば良いだけになりました。
光路差の求め方と近似の利用
光路差の求め方を<図7>を見ながら解説していきます。

<図7>
基本的な手順は2つの三角形が相似であることと
三角比を利用して計算するのですが、
問題はθが分からない事です。
与えられている長さは
$$S_{1},とS_{2}間の距離d、$$
スリット2からスクリーンまでの距離L、スクリーンの中心OからPまでの距離xです。
まず、このスリット2とスクリーンの間の距離と、OP間の距離の差が極めて大きく、実際には非常に細長い三角形になっています。

<図8>
したがって、θは≒0°とみなすことが出来、この時、sinθ≒tanθと近似出来ます。
<図9>中のsinとtanのグラフ(一部)を見て下さい。θ≒0の時ほぼ重なっていますね?)
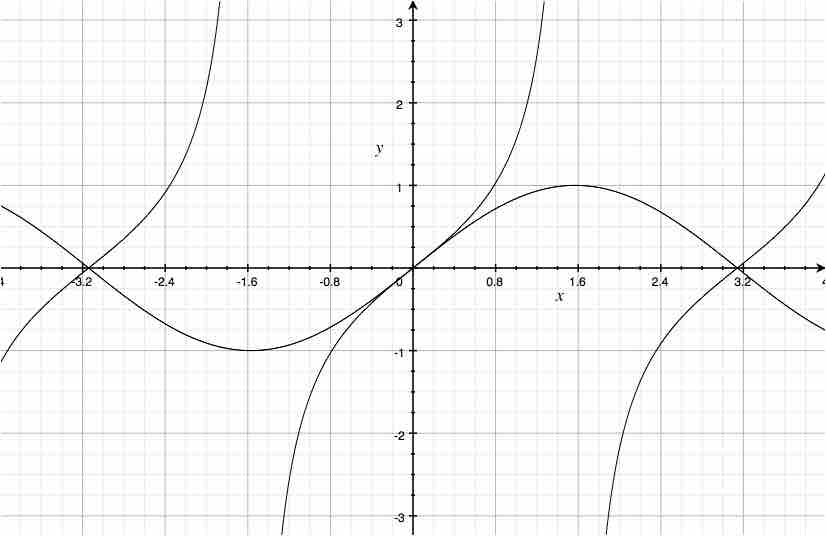
<図9>
sinθ≒tanθと近似できるので、$$\tan \theta =\frac {x}{L}$$
$$これより、光路差=d\sin \theta $$
$$=d\frac {x}{L}=m\lambda (mは0,1,2...整数)の時、$$
Pの位置が明るくなる(これを明線条件と言います)。
今回の各実験の具体的な問題とその解き方は次回詳しく説明します。
今は「光路差の計算」と波長λ、「位相」が揃っているかいないか、が干渉実験全てに共通する最重要事項という事を頭に入れておいてください。
物理でよく使う近似
高校物理では、波動だけでなくその他の分野でも近似を良く使用します。
従って、以下の2パターン(上二つと3番目)近似は覚えておくと良いです。
(但し、近似は複数あるため問題中に従うべき近似が書かれていたら、必ずそれに従って下さい。)
<パターン1>
θ≒0の時sinθ≒tanθ
θ≒0の時 cosθ≒1
<パターン2>
$$(1+x)^{n}≒1+nx$$
まとめと次回予告
今回は薄膜による干渉実験・ヤングの二重スリット実験・くさび形空気層実験を解説しました。
・位相と光路差をチェック
・波長の整数倍か、否かと位相が揃っているか、πズレているかをチェック
・薄膜による干渉実験では、光路差の求め方に注意
・ヤングの二重スリット実験の特徴と、理由をチェック
・物理で必須の近似の練習になるので、ヤングの実験の問題を何度も自分で解いてみる。
次回予告と波の分野で必見の記事
・次回は残りのニュートンリング・回折格子と今回の内容を使った練習問題を解いて更に具体的に解説していきます。
続編「第二回:ニュートンリングと回折格子(光波の干渉2)」を読む!
波動が苦手な人は、以下の分野も苦手意識を持っていることが多いので合わせてご覧ください。
今回も最後までご覧いただき有難うございました。お役に立ちましたら、SNSでシェア&当サイト公式Twitterのフォローをお願いします!
質問・記事について・誤植・その他のお問い合わせはコメント欄、お問い合わせページ、もしくは公式Twitterまでお願い致します。
(*補足1)
<高校範囲外>同位相にできる理由:コヒーレント光にするとも言えます。一般に可干渉性光にするという意味ですが、大学入試ではまず必要ありません。量子力学にも関わってくるので、興味があれば大学で学んでみて下さい。<高校範囲外以上>

