アインシュタインとド・ブロイが切り拓いたミクロでマクロな世界〜
高校物理の中でも原子分野は異質でミステリアスな感じを受けます。
この分野では一般的な常識が通用しない(直感に反する)ことが多い為、取っつきにくい人が多い様に見受けられます。
しかしながら、少なくとも高校での原子範囲は少しの原子/核知識があれば、残りはこれまでの力学と波動を使うだけなので、最初の違和感を乗り越えられると後は比較的楽です。
目次(タップした所へ飛びます)
原子第一回:光の粒子性と波動性の共存
について扱います。
文頭にも書いた様に、高校範囲では原子分野だけが現代物理学、それ以外が古典物理学と分けられます。
その最大の貢献者の1人がアインシュタインです。彼はe=mc^2の式や相対性理論が有名ですが、「光電効果の理論」でノーベル物理学賞を受賞しています。
”光の粒子性と波動性の共存”
なんて難しく書きましたが、
要するに光はボールの様な形のあるものでもあるし、波でもあるよ〜〜と言う事です。
徐々に分かって来るので心配不要です!
光と原子物理で使う定数・単位
アインシュタインは、これまで波であると皆が思っていた光に粒ー光子ーとしての性質も併せ持っていると言うアイデアを思いつきます。
最初に光子に関係する文字をまとめます。はじめから全て覚えようとしなくて構いません!
よく見ると、波動で習った振動数や波長と、「力学(復習用解説記事)」で習った速度(光速)・運動量・運動エネルギー
が入っています。
・光の振動数ν(ニュー)[Hz]、
・波長λ(ラムダ)[m]、
・プランク定数h[Js ]、
・光速c[m/s]とすると
・光の運動量p=h/λ [ kgm/s ] 、
・運動エネルギーE=hν[J]
と表します。
これで波であった光を粒子としても扱える様になりました。
そしてもう一つ「光の強さ」と言う概念が有り、I=Nhν (Iが光の強さ、Nが1秒当りの光子数)で表せます。
これは光子一つのエネルギーの総和を意味します。
さて、やっと光電効果に入れます。
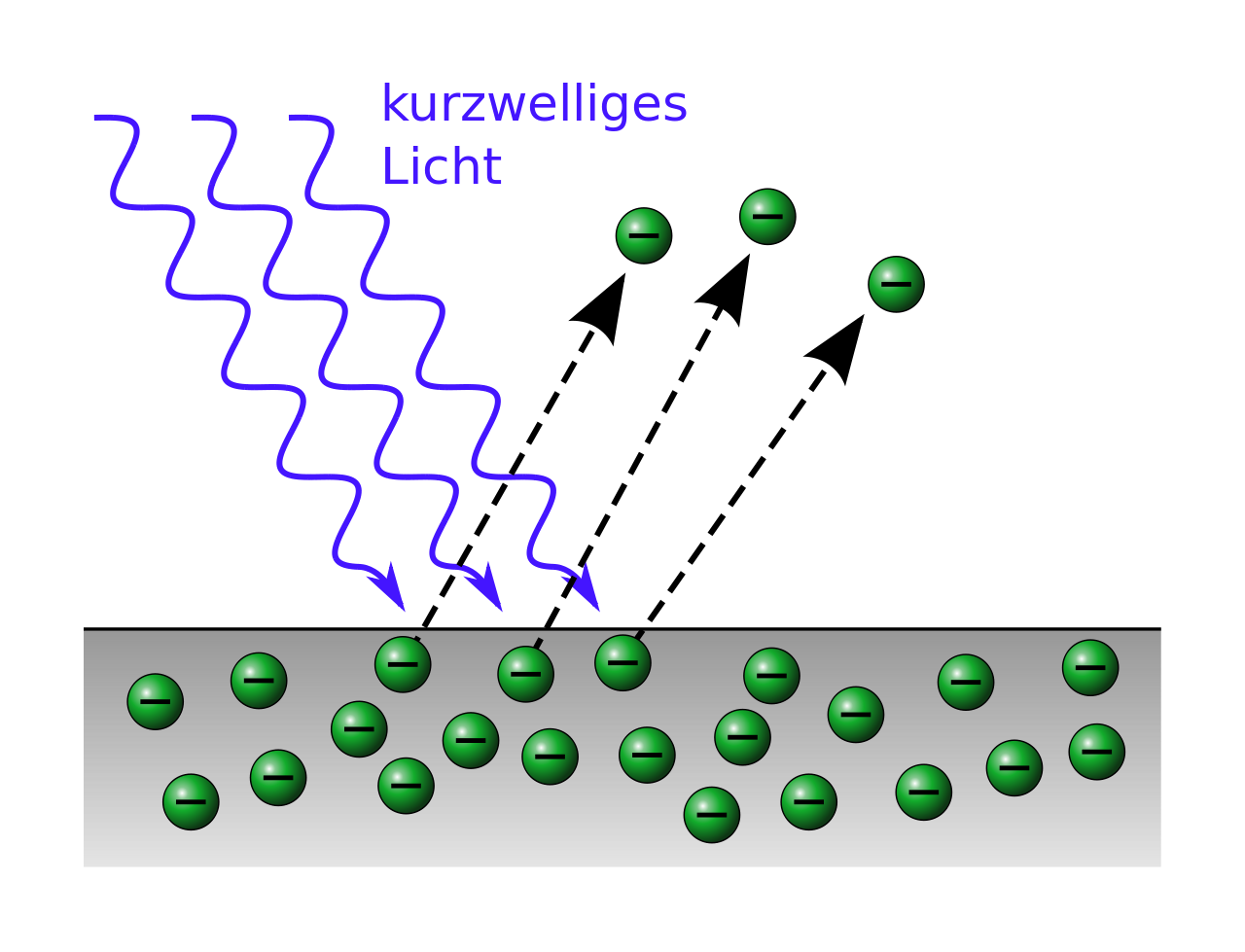
光電効果とは?
、光が波の性質だけしか持っていないとすると矛盾してしまう「井戸型ポテンシャル」を使って説明されます。
井戸型ポテンシャルを説明する為に、深い(ここでは深さをWとします)
井戸の底にサッカーボールが転がっている状況をイメージをしてみて下さい。
もし光が波だけの性質であれば、井戸の上から波を送り続けると、いつかサッカーボールはエネルギーを蓄えて飛び出してくるはずです。
しかし現実にはどれ程強い光を与え続けても、ν(光の振動数)が一定以下の時はサッカーボールは飛び出して来なかった=高さWを超えられなかったのです。
そこで、光が粒子(光電子)であるというアイデアが生まれます。
光がbb弾の様な小さな粒であれば、井戸の上からどれだけサッカーボールをうっても井戸から飛び出して来ません。
しかし、大砲のような弾を上からうつと衝撃でサッカーボールは跳ね上がってくるでしょう。
ここでのbb弾と大砲の弾が光子(光電子)にあたり、弾の大きさがν(光の振動数)と言えるのです。
仕事関数と光電効果の式
この様に光を粒子と見ると、これまでの光=波の概念では説明出来なかった、井戸型ポテンシャルを理解する事が出来るようになったのです。
そして光電効果の式ができました。
{m(Vmax)^2}/2=hν−W
Wは仕事関数と言います。
この式は、[左辺が質量mの電子の運動エネルギー]=[右辺が光子エネルギー ー 仕事関数]
これはνを変数として仕事関数Wを切片とした一次関数のグラフで表せます。
(分からない場合は、左辺の運動エネルギーをy、右辺のνをx、hをa、Wをbとした
y=ax-bと比べてみて下さい。下の図と同じ事です。)
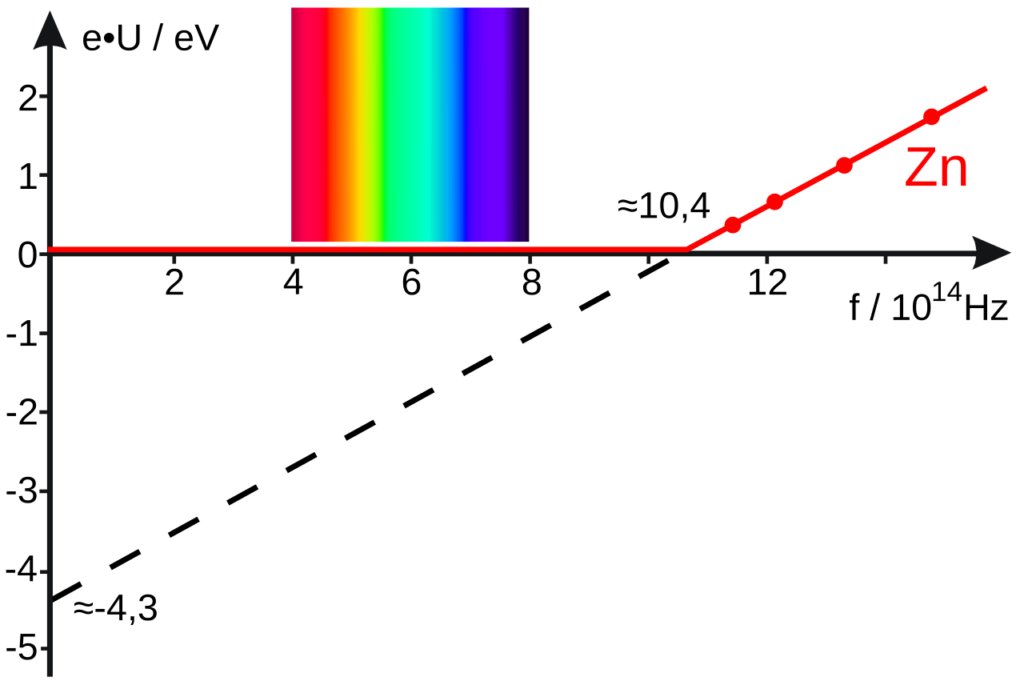
image byKlaus-Dieter Keller
そして運動エネルギー=0の時のνの値をν0とかき限界振動数と言われます。
つまり、先程の井戸型ポテンシャルの例で言う所のサッカーボールが飛び出してくる最小の弾の大きさがν0ということです。
更にν=0の時の切片- Wが井戸の深さを表します。
光電効果の小まとめ
・金属にλが短い電磁波(光、X線、他)をあてると金属より電子が飛び出す。
・但し、限界振動数ν0(Hz)以下の光はどれ程強く、また時間をかけても飛び出さない。
・この飛び出す為に必要な”高さ“をW(J)で表し仕事関数と言う。
・更に、(電子の最大の運動エネルギー)=(光の持ったエネルギー)一(仕事関数)の式が成立する。
コレはつまり
<例>深さが80の井戸に落ちている電子を100の光エネルギーをぶつけると、
20の運動エネルギーを持った電子が弾き出される、という意味です。
今回はここまでとします。
中々理解しにくい&ヘビーな単元ですが、井戸型ポテンシャルの話を思い浮かべつつ、必要ならば何度もこの記事を読んで復習しておいて下さい。
第2回ではコンプトン効果を扱います。
高校物理原子分野解説シリーズ
第2回コンプトン効果がわかる!複雑な式変形や近似の使い方も徹底解説!
第3回
第4回
お役に立ちましたら、はてブ、他を押してシェア&Twitter(リンク)からフォローをお願いしますm(_ _)m。