コンプトン効果
第2回は、光電効果と共に、光の粒子性を証明したもう一つの実験であるコンプトン効果を解説します。
特にコンプトン効果の例題ではかなり丁寧に式変形まで解説をのせているので、
この記事をマスターすれば、光電効果とコンプトン効果はほぼ理解し、得点源にできる筈です!
ぜひ頑張りましょう。
原子物理第一回を未読の方は下リンクより先に第一回を読んでから、このページをご覧下さい。
コンプトン効果とは
コンプトン効果とは、電磁波(X線)を静止している電子に当てて、その前後の電子とX線の様子を見ると、後のX線の方の波長が少し長くなっている現象を言います。
もしX線(電磁波)が波だけならば、前後でλが変化する筈がない事から、光電効果と並んで電磁波が粒子でもあるという粒子と波動の二重性を示す重要な現象です。
具体的には、力学の非弾性衝突と問題はよくにていると言えます。
コンプトン効果の実験
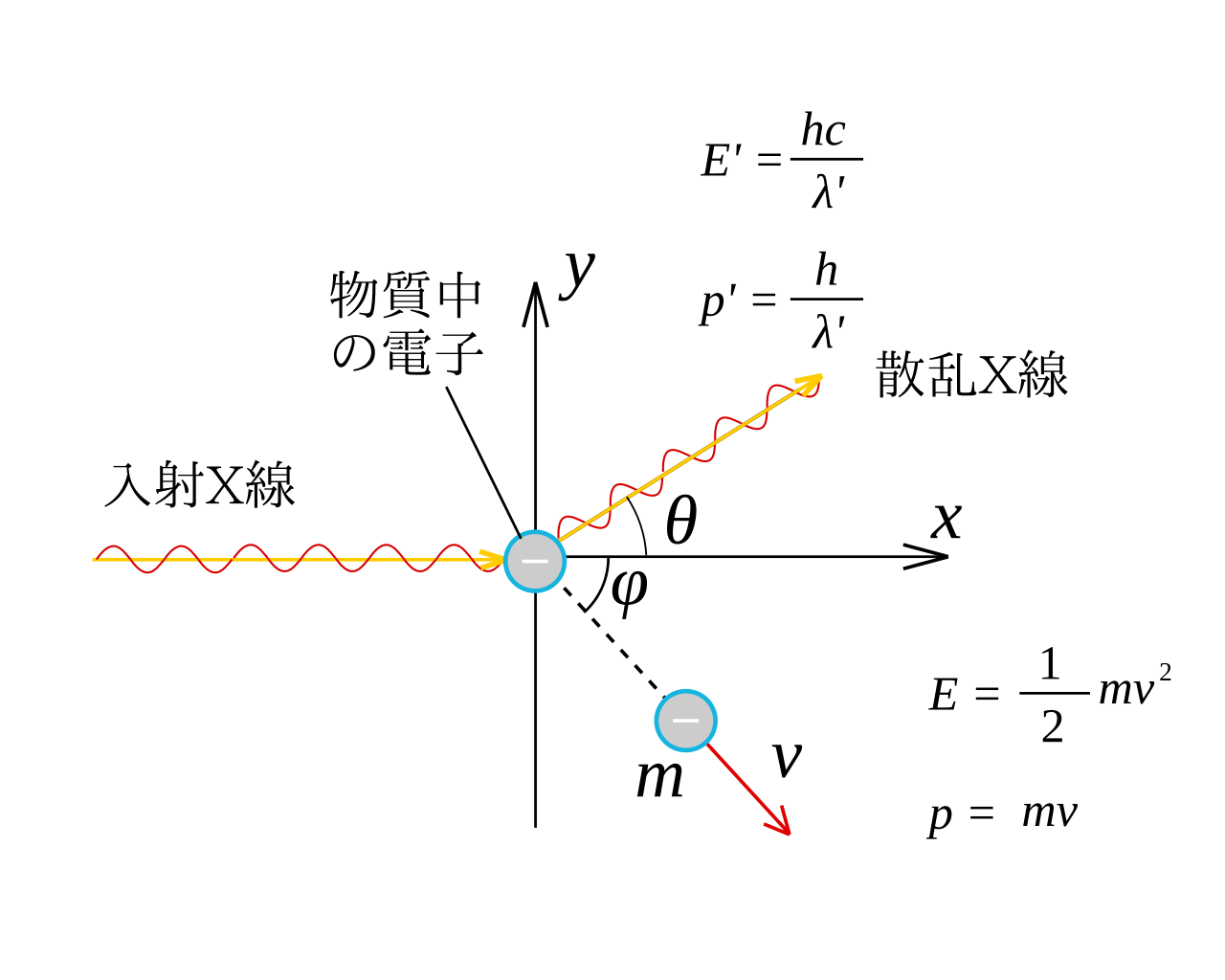
xy平面上の原点に質量mの電子を置き、x軸のマイナス方向から波長がλ、振動数νのX線を当てます。
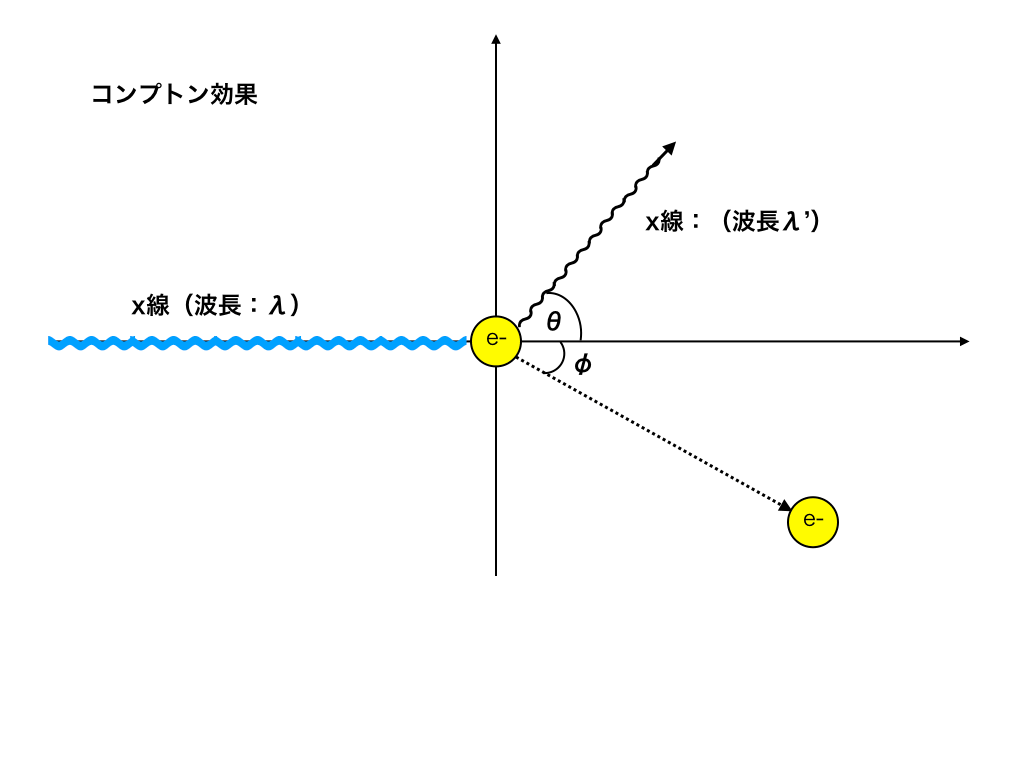
<コンプトン効果図解>
X線が電子に衝突した時、電子は図3のように時計回りにφの向きに速さvで進み、
X線はx軸から反時計回りにθの向きに進みます。この時僅かに波長が変化しλ’になります。
二次元上での非弾性衝突の時の式の立て方は覚えているでしょうか?
この場合3つの式を立てます。
・一つ、衝突前後のエネルギー保存則
・一つ、x軸正方向での運動量保存則
・一つ、y軸正方向での運動量保存則
これらと、近似が与えられるのでそれらを合わせて4つで主に波長の変化を問われる事が多いです。
コンプトン効果の例題
(問)図3のように、電子にX線をあてると
X線の波長が僅かに変化した。
その変化Δλの値を求めよ。
$$ただし、\frac {λ '}{\lambda}+\frac {\lambda}{λ'}≒ 2$$と近似して良い。
ここから複雑な式変形がつづくので、出来ればペンを持って式を追うようにしてみて下さい。
3つの式から不要な文字や自分でおいた文字を消し、近似が使える様に式変形していきます。
<<下の画像>>この辺りは慣れが大事な部分もあるので、大変ですが必ず自分で計算をしてみて下さい。
エネルギー保存則の利用
エネルギー保存より、
$$\frac {hc}{λ}=\frac {hc}{λ'}+\frac {m}{2}v^{2}・・1$$
運動量保存(x軸)の利用
より、
$$\frac {h}{λ}=\frac {h\cos \theta }{λ'}+mv\cos \phi ・・2$$
運動量保存(y軸)の利用
より、
$$0=\frac {h\sin \theta }{λ'}-mv\sin \phi ・・3$$
ここで、\(\sin^{2}\phi +\cos^{2}\phi =1を使って\phi \)を消します。
2の二乗+3の二乗:
(お願い:計算式が長いので、見切れてしまう場合は、スマホを横にしてご覧下さい)
$$\begin{aligned}( mv\cos \phi) ^{2}+( mv\sin \phi) ^{2}=( \frac {h\sin \theta }{λ'}) ^{2}\\
+( \frac {h}{λ}-\frac {h}{λ '}\cos \theta ) ^{2}\end{aligned}$$
$$\begin{aligned}( mv) ^{2}( \sin ^{2}\phi +\cos ^{2}\phi ) =\{(\frac {h}{λ'})^{2}( \sin^{2}\theta )+( \frac {h}{λ'})^{2}\cos^{2}\theta\} \\
+(\frac {h}{λ})^{2}-(\frac {2h^{2}}{\lambda\lambda'}\cos\theta ) \end{aligned}$$
ここで\(sin^{2}\phi +cos^{2}\phi =1\)を使って
$$( mv) ^{2}=( \frac {h}{λ'}) ^{2}-( \frac {2h^{2}}{λλ'}\cos \theta ) +( \frac {h}{\lambda})^{2}・・4$$
1より、1の両辺にmをかけて\(mv^{2}\)を作り、
$$(mv)^{2}=2mhc( \frac {1}{λ }-\frac {1}{λ'}) $$
・・・5
4、5より
$$2mhc( \frac {1}{λ}-\frac {1}{λ'}) =( \frac {h}{λ}) ^{2}-( \frac {2h^{2}\cos \theta }{λλ '}) +( \frac {h}{λ'}) ^{2} $$
・・・6
6の両辺を2mchでわって、
$$( \frac {1}{λ}-\frac {1}{λ'}) =\frac {h}{2mc}( \frac {( λ') ^{2}+(λ) ^{2}}{( λλ') ^{2}}-\frac {2\cos \theta }{λλ '}) $$
・・・7
$$7より、\frac {λ '-λ }{λ 'λ }=\frac {h}{2mcλ’λ}( \frac {( λ') ^{2}+λ^{2}}{λλ'}-2\cos \theta)$$
・・・8
求めるのは、\(\Deltaλ=λ'-λ \) であるから、両辺に( λλ') を掛けて、
$$λ '-λ =\frac {h}{2mc}( \frac {( λ') ^{2}+λ^{2}}{λλ'}-2\cos \theta )$$
・・・9
近似の利用
ここで、問題文で与えられている近似より、
$$\frac {λ '}{λ }+\frac {λ }{λ'} ≒2$$
・・・10
$$10を変形して、⇔ \frac {(λ ') ^{2}+λ^{2}}{λλ '}≒ 2$$
・・・11
9に11を代入すると、
$$\Deltaλ =λ '-λ ≒ \frac {h}{2mc}( 2-2\cos \theta) $$
$$よって、⇔ \Delta λ=\frac {h}{mc}( 1-\cos \theta) $$
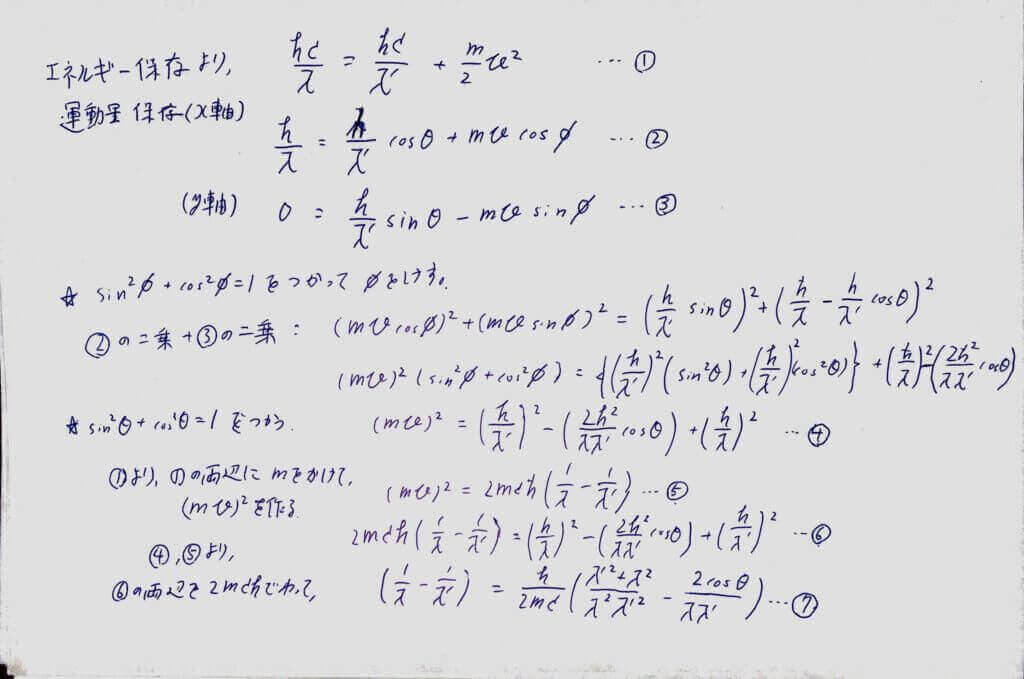

上の様に計算を進めます。最後に近似計算をしてΔλ=の形にして終了です。
このコンプトン効果の問題が解ければ、後は近似として与えられる式が少し違ったり、
文字に具体的な数値が入ったりするだけで、コンプトン効果はほぼクリアしたと言えます!
もし計算など質問があれば、コメント欄までお願いします。
又、Twitterでは、毎日記事更新情報や受験テクニック、お役立ち情報などを呟いています→(当サイト公式Twitterへリンク)
高校物理原子分野シリーズ
第二回:今ここです。
今回の内容が良ければ、第三回へ進んで下さい。
第三回:ド・ブロイ波とボーアの量子条件の理解と、水素原子の構造に迫ります
第四回:水素原子のエネルギー準位と高校化学のイオン化エネルギーがつながります

