〜若き公子ルイ・ド・ブロイとボーア、アインシュタインそして現代物理学へ〜
さて今日は原子物理第3回です。
今日の学習後できるようになる事
・ド・ブロイの考えた物質波が歴史の流れと共に理解できます
・いきなり登場するボーアの量子条件と、物質波の関連が分かります
・化学でも学んだ、電子殻K殻L殻M殻・・・の意味が判明します
・水素原子の軌道半径が求められるようになります
目次(タップした所へ飛びます)
物質波(ド・ブロイ波)とボーアの量子条件を扱います。
第1回と第2回を未読の方は必ず読んでおいてください。
原子物理第一回:「光電効果とは?例え話で原子物理の違和感なくします!」
原子物理第二回:「コンプトン効果がわかる!複雑な計算や近似の使い方も徹底フォロー」
第1回、第2回で、光電効果とコンプトン効果の解説を行いました。
アインシュタインによる「光 は波で有るだけではなく、粒子でもある」という<光の粒子と波動の二重性>のアイデアにより、
2 つの現象が矛盾無く説明出来る様に成ったのでした。
ルイ・ド・ブロイの登場と物質波の仮説
その数年後、アインシュタインとコンプトンの影響を受けたフランスの名門貴族、ブロイ公爵家 の公子ルイ・ド・ブロイが一本の博士論文を書き上げます。
そこには物質波について、~粒子は全て波でもある~
つまりアインシュタインが考案した、波=粒子の概念に対して、それならば粒子=波では無いか?という仮説が立てられていました。
この様な考え方をアナロジー(類推)と呼びます。
論文は斬新かつ難解なもので、提出された教授陣も完全には理解出来ず、アインシュタインに意見 を求めたところ「この青年は博士号よりノーベル賞を受けるに値する」
との返答を受けたと言う逸話が残っています。
果たして5年後ルイは実際にノーベル物理学賞を受賞しました。
物質波の式を見ていきましょう。
質量と波長が結び付けられた式になっているのがわかります。
ド・ブロイ波とも呼ばれるこの波は、粒子の質量をm[kg] 、速さをv[m/s]、波長をλ[m/s]、運動量p=mv[kgm/s]として以下の式を満たします。
λ=h/p= h/mv
ではココからはドブロイ波を既知として水素原子の構造に迫ります。
一般に電球や太陽光などは連続的なスペクトルを描きます。(プリズムを通して虹色に成る事を想像して 下さい)

しかし水素原子を放電管へ入れて放電するととびとびの線スペクトルが出てきてしまうのです。
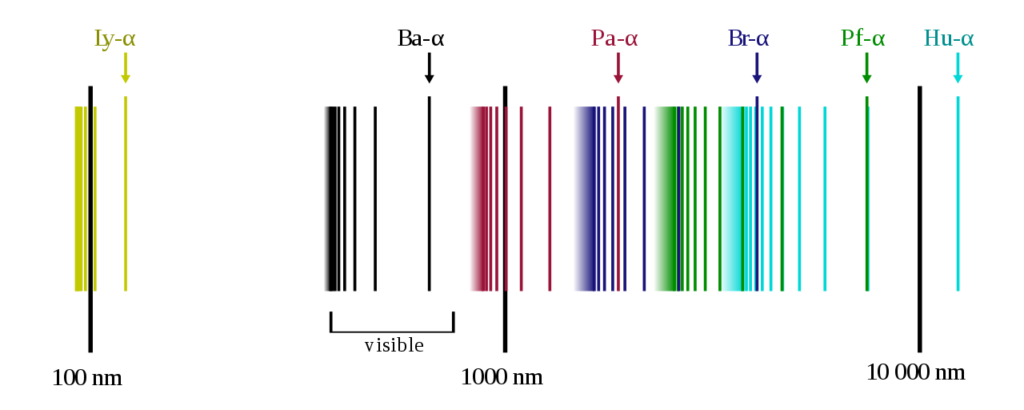
image by OrangeDog
これは水素がある非連続な振動数、波長しか出てこないという事です。
※<コラム>ちなみに非連続な事を離散的と言います。
例えば数学で数列はn=1、2、3、、、とびとびの時のAnを求めますよね?n=1.5番目の数を 求めよ、などは有り得ません。
何故水素は離散的な波長の光しか発しないのか?
その謎を解くには水素原子の軌道とエネルギー準位の事を知らなければならないのです。
(第3回では、記事の都合上”水素原子の軌道“まで解説し、
第4回でエネルギー準位を説明、そして謎を解明します。)
水素原子の軌道(電子軌道の事です)を知る為には、ボーアの量子条件と等速円運動を用いる必要があります。
突然「ボーアの量子条件」などが登場して戸惑っているかと思います。
「ドブロイ波と何の関係があるのか?」 それはもっともな疑問です。
本来ボーアの量子条件が先に発表されているので、それを学んだ後、ド・ブロイ波を導入すべきなのですが、高校レベルの数学/物理では歴史通りの教え方が出来ないのです。
その為やむを得ず、順序を無視してボーアの量子条件にドブロイ波の式を組み込んで説明しています。
ボーアの量子条件とは
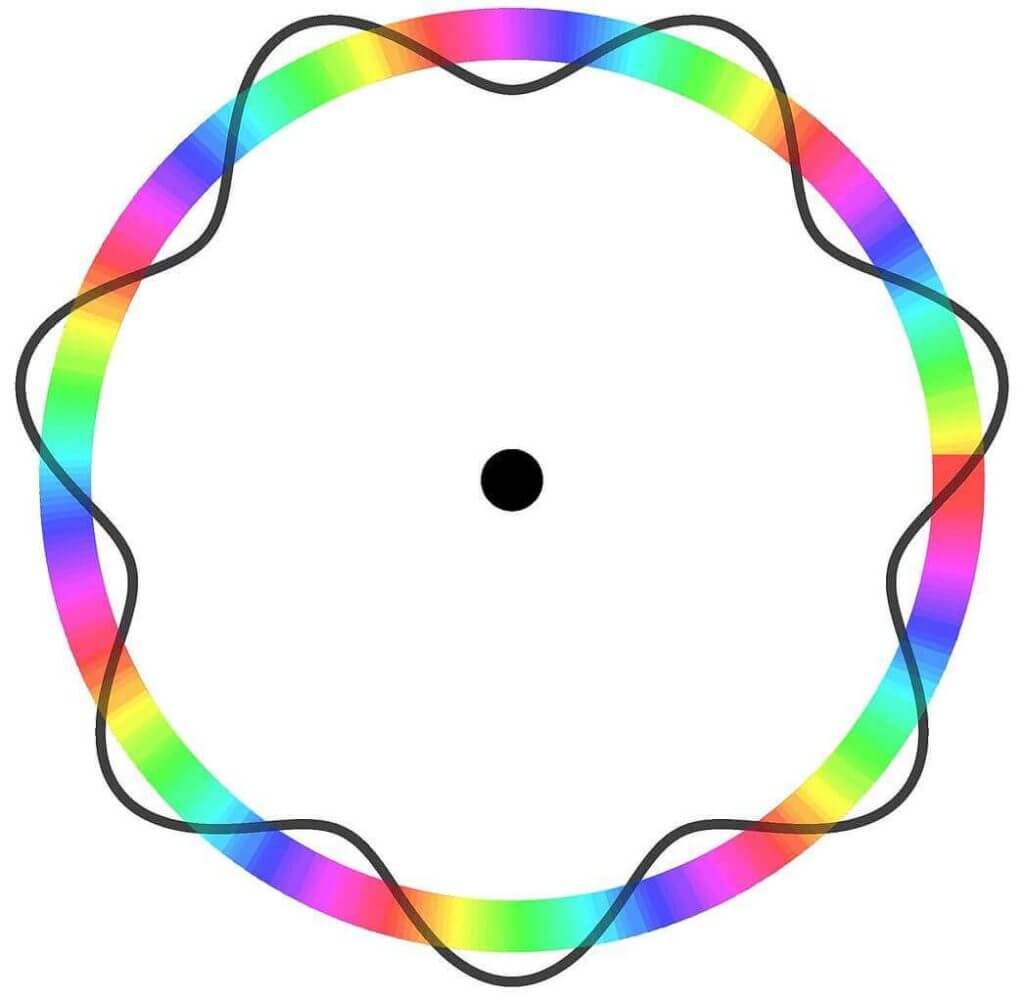
ボーアの量子条件とは、「電子軌道が存在する条件は円軌道の長さがドブロイ波の波長の整数倍である事」です、
つまり軌道の長さを2πrとすると下の様に書けます。
2πr=nλ=nh/mv(但しhはプランク定数、またn=1,2,3...)、、、#1
一方で水素原子は原子核の周りを電子が一個回っている事から、
電子の振る舞いはクーロン力を 向心力とした等速円運動の式で表せます。
これは簡単なはず。 mv 2/r=ke2/r2、、、#2
半径rの円軌道を電子e-が速さv、質量mでまわっている式です。
後は#1と#2を連立してvを消して、r=の形にします。
rは軌道半径で、右辺に離散的な自然数nが入っているので、左辺rに添字としてn(n=1,2,3,....)を 書いておきます。
以下に軌道半径の計算&式を載せておきます。

写真の様に水素原子の軌道半径を求める事ができました
$$r_{n}=\frac {h^{2}( n^{2}) }{4\pi ^{2}kme^{2}}$$
この式のn=1を入れると皆さんの知っているK殻
n=2をいれるとL殻
n=3を入れるとM殻・・・の軌道半径になるのです!
だんだんと物理と化学が繋がり始めたのが分かりますでしょうか?
まとめと次回予告
次回はいよいよこれまでの知識をもとに、水素原子が線スペクトルを発する理由である"エネルギー準位"や"電子の落下と光の放出"など核心に迫っていきます。
始めは理解しにくい分野ですが、何度も勉強していくうちに、いろいろな事が繋がって面白くなってきます!
是非、このサイトを利用して高校物理最後の分野にして、現代物理学のはじまりである原子分野を攻略しましょう。
原子物理シリーズ一覧
原子物理第一回:「光電効果とは?例え話で原子物理の違和感なくします!」
原子物理第二回:「コンプトン効果がわかる!複雑な計算や近似の使い方も徹底フォロー」
第4回(水素原子の構造とエネルギー準位・高校物理と化学の融合)を作成しました。
原子物理第四回:「水素原子のエネルギー準位とイオン化エネルギーの正体:高校化学との融合」
お役に立ちましたら、下のソーシャルボタンでシェア&このサイトの公式Twitterのフォローをお願いしますm(_ _)m

