
二項定理・多項定理はこんなに単純!
二項定理に苦手意識を持っていませんか?
教科書や参考書には、二項定理の難しそうな数式ばかりの公式が並んでいて、見るのも嫌だ!と避けている人も多いのではないでしょうか。
しかし、残念ながら数学では非常に大切な定理なので逃げることはできません。
特に理系ならば、数Ⅲの極限や微分・積分の応用の証明などで必須になってきますし
(記事の最後に、二項定理と極限・積分との融合問題の解説記事をまとめています)
文系でもこの定理を利用する出題はかなり多いのです。
でもご安心下さい、一見ややこしく見える数式ですが、この記事を読み終わる頃にはただの組み合わせ(しかも簡単な)であることがわかるようになります。
目次(タップした所へ飛びます)
二項定理の公式の意味とは
教科書では、二項定理と多項定理は別々の公式が書いてありますが、
この記事ではまず二項定理の考え方・意味を紹介し、
引き続いて、多項定理が実質的に同じものであるということと、覚えるコツを解説していきます。
(実際には考え方が理解出来ていれば「覚える」必要すらないです。いつでも導き出せるからです。)
二項定理とは
早速始めます。教科書には下の様な複雑な公式が書いてあると思います。
$$\left( a+b\right) ^{n}=\sum ^{n}_{k=0}nC_{k}a^{n-k}b^{k}$$
これでは、ニガテ意識を持つ人が多いのも当然です。筆者も初めて見た時はウンザリしました。
式を展開して具体的に考える
(a+b)の3乗の場合の時、実際に式を並べて展開してみると、
\((a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\)・・・#1 となります。
この様に3乗くらいならば、展開してもそれほど大変では無いですが、4乗、5乗、・・・となると
お手上げです。また、\((a+b)^{9}を展開した時a^{3}b^{6}\)の係数を求めよ、などと言う問題が出題されますが、
実際に展開してa3b6の係数を求めていたらテストが終わってしまいます!!
そこで、二項定理の公式を知っていれば、簡単に求めることができます。
しかし公式丸暗記では、忘れやすい上応用も利かなくなるので理屈を理解してもらう必要があります。
二項定理の公式にC(コンビネーション)が出てくる理由
#1の右辺の各項の係数を見ると、(1、3、3、1)
となっています。これはaの三乗を作るためには
(a+b) (a+b) (a+b)の中からa掛けるa掛けるaを選び出すしか無く、その場合の数を求める為にCを使っているのです。
この場合では1通りなので(1)・(a^3)となっています。
同様に、 a2bの係数を考えると、(a+b) (a+b) (a+b)から、【aを2つとbを1つ】選ぶ場合の数を求めるので3C2が係数になります。

二項係数・一般項の意味
この様に、各項の係数の内、nCkのえらび方(a,bの組み合わせの数)の部分を二項係数と呼びます。
そして、二項定理の公式のうち、シグマの右側にあった\(nC_{k}a^{n-k}b^{k}\)のことを一般項と呼びます。
では、どのような式を展開した項も二項係数のみがその係数になるのでしょうか?
残念ながら、ある項の係数は二項係数だけでは正しく表すことができません。
なぜなら、公式:(a+b)nの aやbに係数が付いていることがあるからです。
例:(a+2b)n 下で実際に見てみましょう。
( a+2b)3の式を展開した時、ab2の係数を求めよ
先程の式との違いはbが2bになった事だけです。
しかし、単純に3C2=3 よって3が係数 とするとバツです。何故でしょう?
当然、もとの式のbの係数が違うからです。
では、どう計算したらいいのでしょうか?
求めるのは、ab2の係数だから、3つのカッコからaを1個と2bを2個を取り出すので、その条件の下で、\(ab^{2}の係数は(1)a×(2)b×(2)bで(4)ab^{2}\)が出来ます。
そして、その選び方が3C2=3 通り、つまり式を展開すると4ab2が3つ出来るので
\(4ab ^{2}×3=12ab ^{2} \)よって、係数は12 が正しい答えです。
二項係数と一般項の小まとめ
まとめると、(二項係数)×(展開前の文字の係数を問われている回数乗した数)=問われている項の係数
となります。
そして、二項定理の公式のnに具体的な値を入れる前の部分を一般項と呼びます。
・コンビネーションを使う意味
・展開前の文字に係数が付いている時の注意
に気を付けて解答して下さい。
いかがですか?
はじめの暗号のような式に比べて、少しは理解しやすくなったのではないかと思います。
では、二項定理の応用である多項定理に入る前に、パスカルの三角形について紹介しておきます。
パスカルの三角形
パスカルの三角形とは、図一のような数を並べたものです。
ちょうど三角形の辺の部分に1を書いて行き、その間の数を足していくことで、二項係数が現れるというものです。
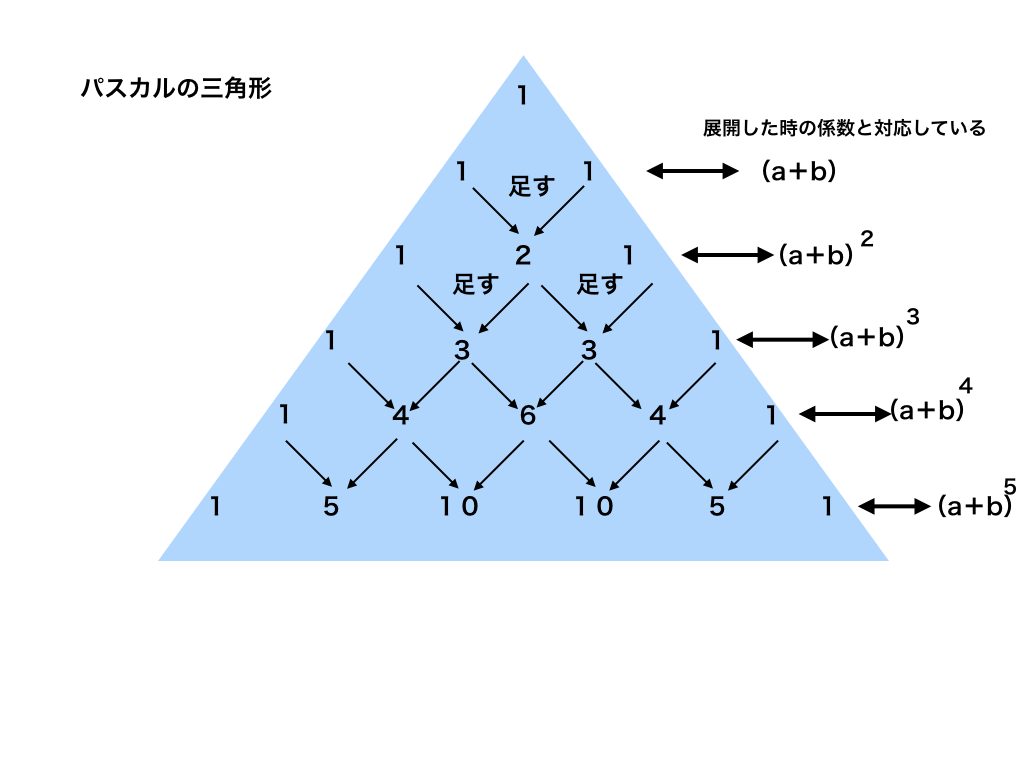
<図:二項定理とパスカルの三角形>
このパスカルの三角形自体は古くから知られていたようですが、論文としてまとめたのが、「人間とは考える葦である」の言葉や、数学・物理学・哲学など数々の業績で有名なパスカルだった為、その名が付いたと言われています。
多項定理とは
二項定理を応用したものとして、多項定理があります。
こちらも苦手な人が多いですが、考え方は二項定理と同じなので、ここまで読み進められたなら簡単に理解できるはずです。
多項定理の公式とその意味
大学入試に於いて多項定理は、主に多項式の◯乗を展開した式の各項の係数を求める際に利用します。
(公式)$$( a+b+c) ^{n}=\sum _{p+q+r=n}\frac {n!}{p!q!r!}a^{p}b^{q}c^{r}$$
今回はカッコの中は3項の式にしています。
この式を分解してみます。この公式の意味は、
\(( a+b+c)^{n}\)を展開した時、
$$一般項が、\frac {n!}{p!q!r!}a^{p}b^{q}c^{r}となり$$
それらの項の総和(=全て展開して同類項をまとめた式)をΣで表せるということです。
いま一般項をよくみてみると、$$\frac {n!}{p!q!r!}a^{p}b^{q}c^{r}$$
$$左の部分\frac {n!}{p!q!r!}$$
は同じものを含む順列の公式と同じなのが分かります。
同じものを含む順列の復習
例題:AAABBCCCCを並べる順列は何通りあるか。
答え:まず分子に9個を別々の文字として並べた順列を計算して(9!)、
分母に実際にはA3つとB2つ、C4つの各々は区別が付かないから、(3!2!4!)
を置いて、9!/(3!2!4!)で割って計算するのでした。
解説:分子の9!通りはA1,A2,A3,B1,B2,C1,C2,C3,C4 、のように同じ文字をあえて区別したと仮定して計算しています。
一方で、実際には添え字の1、2、3,,,は存在しないので(A1,A2,A3),(A2,A1,A3),,,といった同じ文字で重複して計算している分を割っています。
Aは実際には1(通り)の並べ方なのに対して、3!=6(通り)分余計にカウントしているので6で割っています。
同様にBは(B1,B2),(B2,B1)の、2!=2通り、Cは4!=24(通り)分の重複分割ることで、以下の
答え 1260(通り)//となります。
二項定理と多項定理の違い
ではなぜ同じものを含む順列の計算を多項定理で使うのでしょうか?
上記の二項定理の所でのab^2の係数の求め方を思い出すと、
コンビネーションを使って3つの式からa1個とb2個の選び方を計算しました。
$$_{3}C_{2}=\frac {3!}{2!1!}$$
多項定理では文字の選び方にコンビネーションを使うとややこしくなってしまうので、代わりに「同じものを並べる順列」を使用しています。
次に公式の右側を見てみると、各項のp乗q乗r乗(p+q+r=n)となっています。
これは先程同じものを選んだ場合の数に、条件を満たす係数乗したものになっています。
(二項定理では選ぶ項の種類が二個だったので、p乗q乗、p +q=nでしたが、多項定理では選ぶ項の種類分だけ◯乗の数は増えて行きます。)
文字だけでは分かりにくいかと思うので、以下で実例を挙げます。
多項定理の公式の実例
実際に例題を通して確認していきます。
\(( 2x^{2}+x+3)^{3}において、x^{3}\)の係数を求めよ。
多項定理の公式を使っていきますが、場合分けが必要な事に注意します。
(式)を3回並べてみましょう。
\((2x^{2}+x+3)( 2x^{2}+x+3)( 2x^{2}+x+3)\)
そして(式)(式)(式)の中から、x^3となるかけ方を考えると「xを3つ」選ぶ時と、
「2x2を1つ、xを1つ、3を1つ」選ぶ時の2パターンあります。
各々について一般項の公式を利用して、
xを3つ選ぶ時は、
$$\frac {3!}{3!0!0!}× 2^{0}× 1^{3}× 3^{0}=1$$
「2x2を1つ、xを1つ、3を1つ」選ぶ時は、
$$\frac {3!}{1!1!1!}\times 2^{1}\times 1^{1}\times 3^{1}=36$$
従って、1+36=37がx^3の係数である//。
ちなみに、実際に展開してみると、
\(8x^{6}+12x^{5}+42x^{4}+37x^{3}+63x^{2}+27x+27\)
になり、確かに一致します!
この作業では、x^3の係数を求めましたが、最初の公式を使用すれば、いちいち展開しなくても任意の項の係数を求めることが出来る様になり大変便利です。
二項定理まとめと応用編へ
・二項定理では、二項の展開しか扱えなかったが、多項定理を使う事で三項/四項/・・・とどれだけ項数があっても利用できる。
・二項定理のコンビネーションの代わりに「同じものを並べる順列」を利用する。
・多項定理では二項係数の部分が階乗に変化しますが、やっていることはほとんど二項定理と同じ事なので、しっかり二項定理をマスターする様にして下さい!
実際には、〜を展開して全ての項を書け、という問題は少なく、圧倒的に「特定の項の係数を求めさせる問題」が多いので今回の例題をよく復習しておいて下さい!
二項定理・多項定理の関連記事
冒頭でも触れましたが、二項定理は任意の項の係数を求めるだけでなく、数学Ⅲで「はさみうちの原理」や「追い出しの原理」と共に使用して、極限の証明などで大活躍します。↓
「はさみうちの原理と追い出しの原理をうまく使うコツ」ではさみうちの基本的な考え方を理解したら、
「二項定理とはさみうちの原理を使う極限の証明」で、二項定理とはさみうちの原理をあわせて使う方法を身につけてください!
今回も最後までご覧いただき、有難うございました。
質問・記事について・誤植・その他のお問い合わせはコメント欄までお願い致します!

