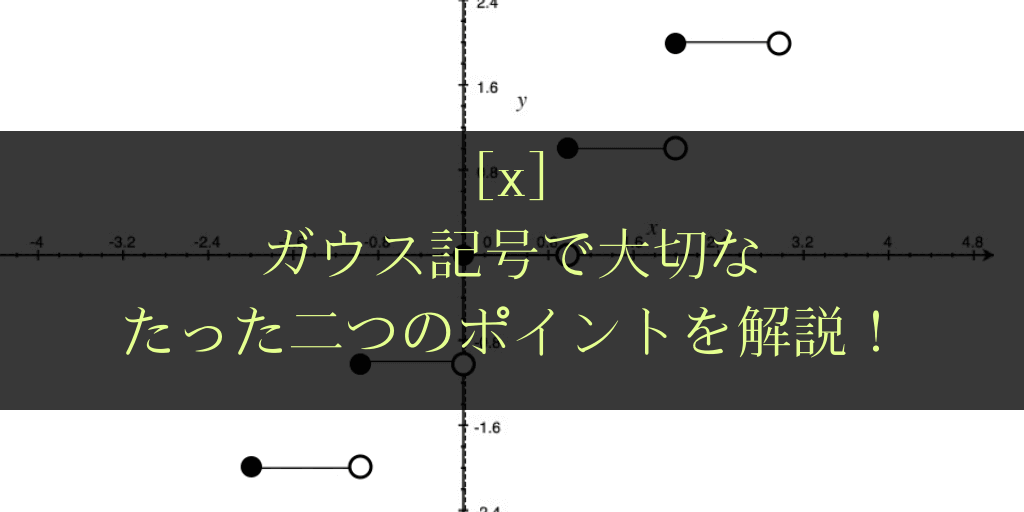
ガウス記号とその攻略法
整数分野のみならず、様々な分野で出現する『ガウス記号』その攻略法を紹介するシリーズ第1弾。
今回は、知識0から始めて、
・ガウス記号の意味
・簡単な方程式、不等式、
・さらにガウス記号の入った2次不等式まで、
「理解すれば怖くない」、[x]:ガウス記号について解説していきます。
(扱う問題は2題だけなので、それほど時間をかけずにガウス記号の扱い方を習得できるはずです。)
目次(タップした所へ飛びます)
ガウス記号の基本
教科書や参考書では、ガウス記号は、[x]のように表記されて、『xを超えない最大の整数』を意味する。
というような説明がされているかと思います。
整数問題に限りませんが、すぐに理解しずらい問題や説明に出くわした時の最良の対処法は、『実験してみる』ことです。
<参考:「難問に当たって解法が思いつかない時の対策(整数・場合の数)」>
ここでは、xに適当な数字を入れてみるのです。
すると、ガウス記号の意味がなんとなくわかってきます。
(例)[3.6]=3 や、[-5.5]=ー6,[ーπ]=[-3.1415,,,]=ー4。
といった具合です。
ガウス記号で重要なたった2つのこと
(一)それは、ガウス記号で表された数は”整数”である!という事です。
当たり前のことなのですが、複雑な問題になるにつれて、目の前の数式に追われてしまい、このことを忘れがちになる人が多いのです。
(二)もう一つは『上手く不等式を利用する』という事です。
(次の項の、ガウス記号を不等式ではさむで解説している『(1)の不等式』と2種類のガウス記号で不等式を作る『(2)の不等式』)
この2つをしっかり意識して問題に臨めば、大抵の問題は解けてしまいます。
では、次の項からガウス記号に関連する不等式を紹介していきます。
ガウス記号で使う不等式
ここでは、問題を解く際に必須の不等式を並べます。
(1):x-1<[x]≦x
(2):[x-1]<x≦[x]
(3):[x]≦x<[x]+1
以上の不等式はほぼ必ず利用します。確実に頭に入れておきたいところです。
不等式をど忘れしてしまった時の対処法
等号の位置や順番、符号がど忘れしてしまった時のために対策を書いておきます。
「適当な数(2.3、-1.8などの小数付きの数と3、-5などの小数なしの整数)をの2種類を代入して確かめてみる」
先ほどの適当な数を入れて実験、と同じことです。わからなくなったらまず実験!これは今後何度も使用します。
ガウス記号の問題
ガウス記号の定義を抑え、大切な2つの事を頭においてここからは実際に問題を解いていきましょう。
ガウス記号入りの方程式・不等式
例題1)[x]=4 のとき、xのとりうる範囲を求めよ。
例題2)\(3[x]^{2}-41[x]+60<0 の時、\)xのとりうる範囲を求めよ。
解答解説1)この例題はガウス記号の意味を理解していれば即解ける問題です。
\([x]≦x<[x]+1より、 4≦ x<5・・・(答)\)
二次不等式の解き方
解説2)一気にレベルアップしたと感じる人もいるかもしれません。
ガウス記号の入った2次不等式ですが、この問題にはガウス記号を攻略するためのエッセンスが凝縮されています。
まずは、普通の不等式と同じように因数分解をしてみましょう。
$$(3[x]-5)([x]-12)<0 ・・・(一)$$
$$⇔\frac{5}{3}<[x]<12・・・(二)$$ここまでは、ガウス記号は関係なく進みます。
次に、(二)の式とガウス記号の性質から、
\(2≦[x]≦11\)・・・(三)が成立することがわかるでしょうか?
つまずくとすれば、2≦xのところと、x≦11のところだと思います。
[x]の値は、初めに『重要な二つのこと』で説明したように、整数でした。
つまり、5/3より大きい最小の整数である『2』と、12未満の最大の整数である『11』で[x]を挟んでいるというだけのことです。
では、次に移ります。
<ポイント:ガウス記号は整数部分と小数部分を分けて考える>
[x]の中身である”x”がちょうど整数でない限り、xは”整数の部分”と、そこから”切り落とされる小数の部分”からできているはずです。(例)[2.4]=2 ですが、2+0.4 という風に考えるのです。
すなわち、xーp=[x]と置くことができます。
(例:2.4-0.4=[2.4])
(ここで、pは0以上1未満)
xから小数部分を引いたものが[x]であるということです。
この式もガウス記号の問題では頻繁に利用するので覚えておきましょう。
では問題に戻ります。
2≦[x]≦11・・・(三)の\([x]にxーp=[x]を代入\)します。
\( 2≦xーp≦11、\)ここで、「p」を左辺と右辺にそれぞれ移行すると、
2+p≦x≦11+p・・・(四)
この式を“2+p≦x ”と“x≦11+p”に分けて考えます。
$$pは0以上1未満より、2+0≦2+p≦x$$
\(⇔2≦x・・・(五)\)
$$x≦11+p、ここでx≦11+p<11+1 $$
\(⇔x<12・・・(六)\)
(六)の式に等号が含まれていないことに注意してください!
pは1”未満”である(小数部分をpと置いたのでした)ことを考えれば当然です。
あとは、(五)と(六)式を合わせれば、
2≦x<12・・・(答)
ただの2次不等式ですが、ガウス記号の扱い方をいろいろと学べることが伝わったかと思います。
まとめと整数分野の関連記事へ
・ガウス記号で兎に角頭に入れておくことは、
・[x]は整数である、
・xを整数部分と小数部分に分けて式を作る
・[x]を挟む不等式と、[x]で挟む不等式の二つ( or三つ)を使う
ということだけです。以上の点をしっかりと理解して覚えておけば、多少ひねられた問題が出ても対応できます。
次回(作成中)は、ガウス記号を利用した約数の個数など、解法として知っておくべき問題を紹介・解説します。
関連記事と整数問題まとめ
>>「整数分野の問題の解法・定石のまとめ11選!閃きなしで攻略する方法」<<
方程式、不等式に関する記事をまとめました(オススメ)
>>「いろいろな方程式・不等式の解き方総まとめ〜二次方程式から微分方程式まで〜」<<
最後までご覧いただきまして、有難うございました。
・「スマナビング!」では読者の皆さんからのご意見や、記事のリクエストをお待ちしています。ぜひコメント欄にお寄せください。
また、snsでいいね!やシェア、B!、Twitterのフォローをしていただけると助かります。

