”電気振動”と”共振”(交流:第二回)
<この記事の内容と対象>:前回「交流回路(一):”RLC”直列回路と”インピーダンス”Z」を読んだ方や、共振・(電気振動・LC回路)の問題が分からない人に向けて、イメージ図を用いながら解説した記事です。
目次(タップした所へ飛びます)
共振とRLC回路での周波数
まずは、共振という現象の意味を【前回のRLC直列回路】について復習しながら見ていきます。
波動の復習と周期・振動数の関係
交流回路では
・”角周波数ω”・“周期T”・“振動数f”などの意味と、
・それぞれの関係式の知識
は必ず必要になるので、次の公式と出来れば「物理:力学の単振動の基本と公式」にも目を通しておいてください。
$$f(Hz)=\frac{1}{T},T=\frac{2\pi}{\omega},(v=f\lambda)$$
共振とは
直流回路における「オームの法則」では、V=IRより、
電流I(A)と抵抗値R(Ω)は電圧V(V)一定のもとで反比例の関係にありました。
交流の場合もそれと同じような考え方で、インピーダンス『Z』が最も小さい時、(交流)電流の大きさは「最大」となります。
インピーダンスZから共振周波数を導く
この状態を『共振』と言い、共振を起こす交流電源の周波数f(Hz)のことを【共振周波数】(そのままです)と言います。
結果
まず、インピーダンスは次のように表せました。$$Z=\sqrt{(\omega L-\frac{1}{\omega C})^{2}+R^{2}}$$
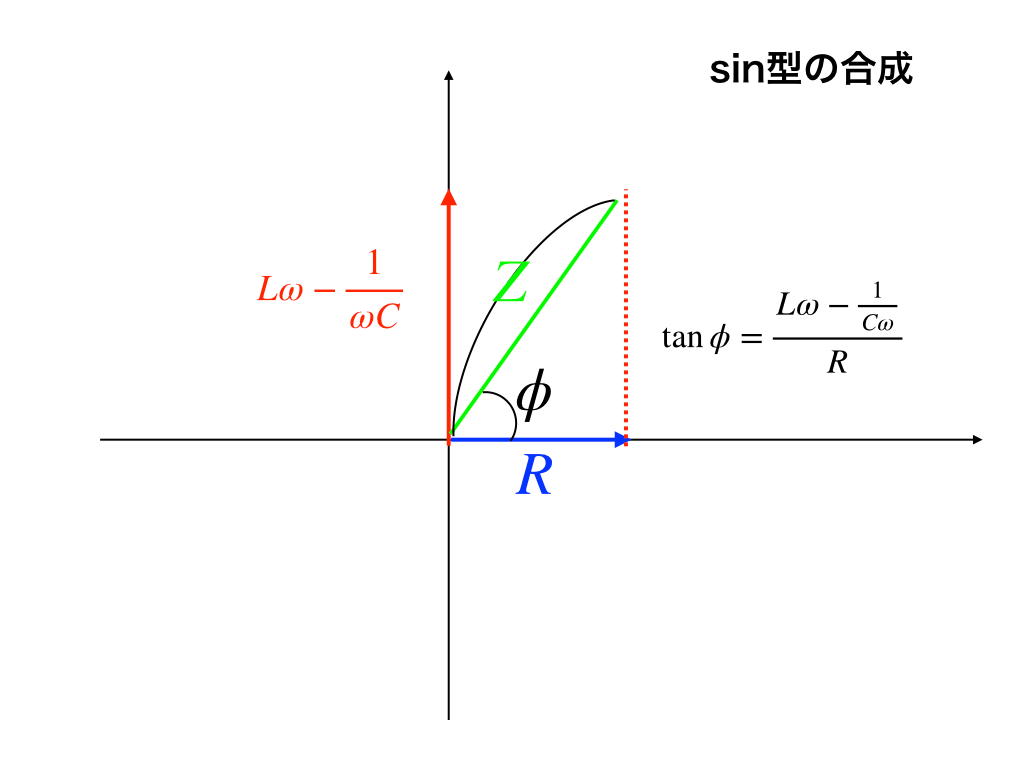
この値を最小にするために出来ることを考えると、R^{2}以外の「引き算の部分」→$$(\omega Lー\frac{1}{\omega C})^{2}$$が最小(=0)になれば良いので、$$\omega L-\frac{1}{\omega C}=0$$
これを解くと、\(\omega=\frac{1}{\sqrt{LC}}\)さらに、fはTの逆数、かつ\(T=\frac{2\pi}{\omega}\)
ゆえに、周波数が$$f=\frac{1}{2\pi \sqrt{LC}}$$の時「共振」が起こります。
電気振動とは何か
次に、交流のメインの一つ『電気振動』に入ります。
LC回路
L:コイル、C:コンデンサーと交流電源からなる回路を考えます。
リアクタンスの復習
コイルの重要な性質として、『電流の流れの変化を妨げる方向に起電力が生じる』というものがありました。$$V_{誘導起電力}(V)=-L\frac{\Delta I(A)}{\Delta t(s)}$$
電気振動の時系列変化
このコイルと、充電済みのコンデンサーを接続すると、以下のstepのように電荷が移動して、極板の+とーが時間とともに繰り返し入れ替わります。
step0:コンデンサに充電しておく
まず電荷を帯びたコンデンサーを用意します。
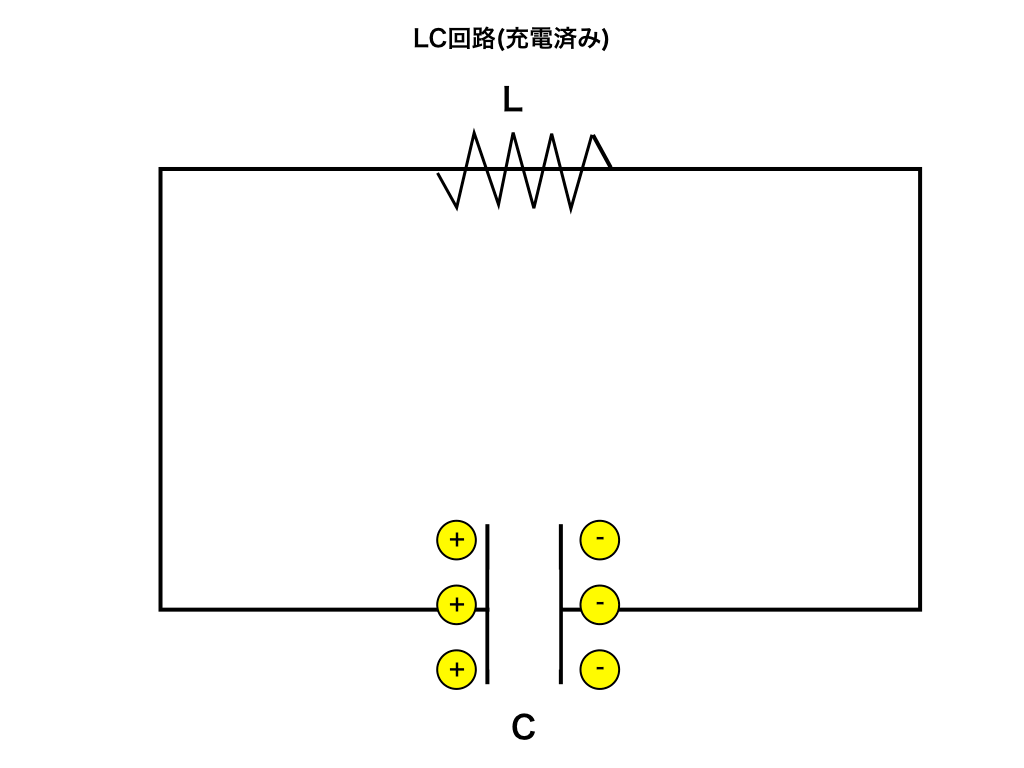
step1:一方向に電荷が動き(電流が流れ)だす
(プラスの電荷は右側の極板・)マイナスの電荷は左側の極板へと移動していきます。
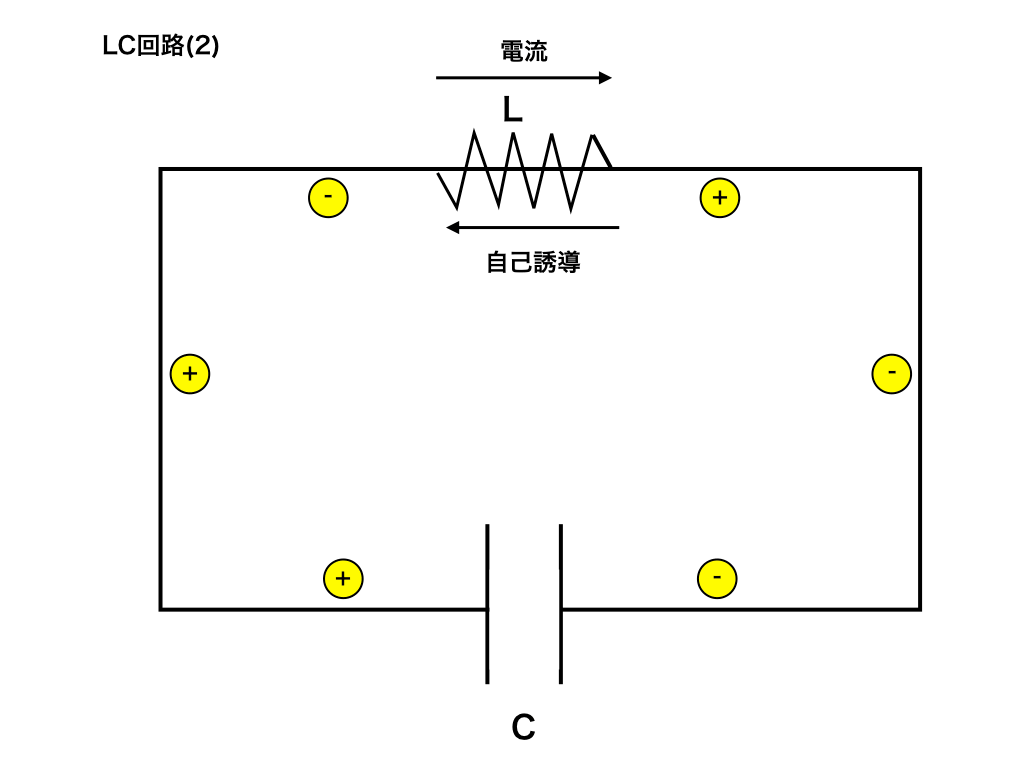
この時、電流の変化を邪魔するように、コイルで自己誘導による起電力が生じます。
step2:一旦全ての電荷が逆側の極板にたまる
しばらくすると、はじめの状態と真逆の電荷を2枚の極板が帯びます。
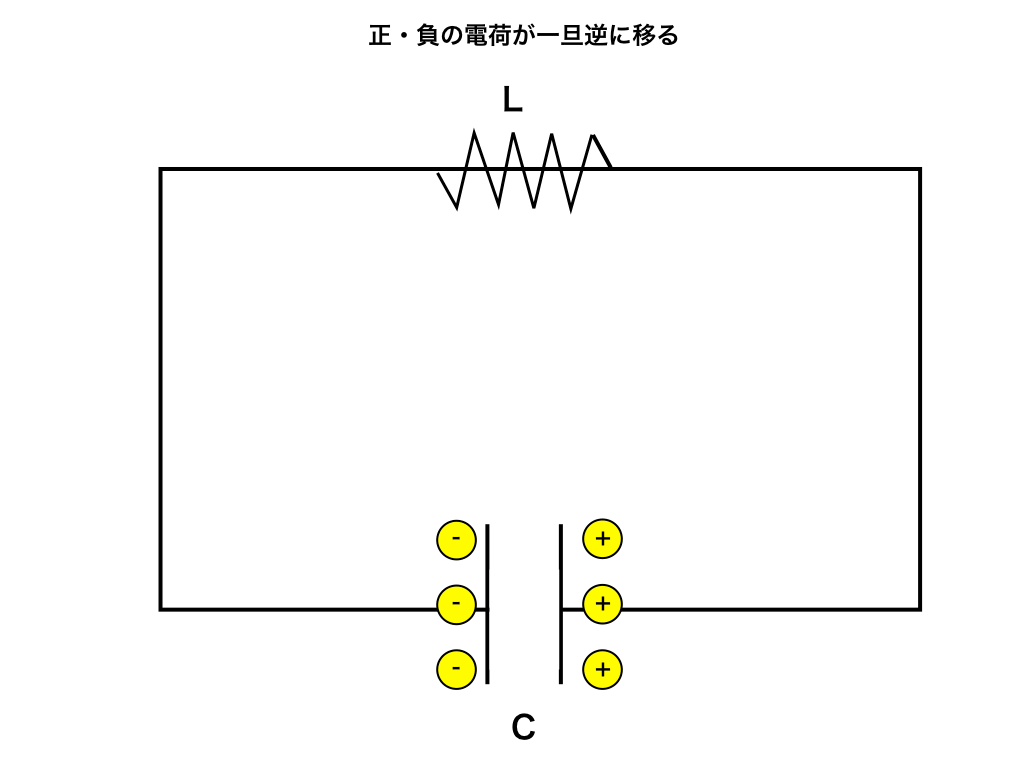
step4:初めと逆方向に電荷が動き(電流が流れ)出す
今度はstep1と逆向きに電流が流れ、”自己”誘導起電力の向きも逆になります。
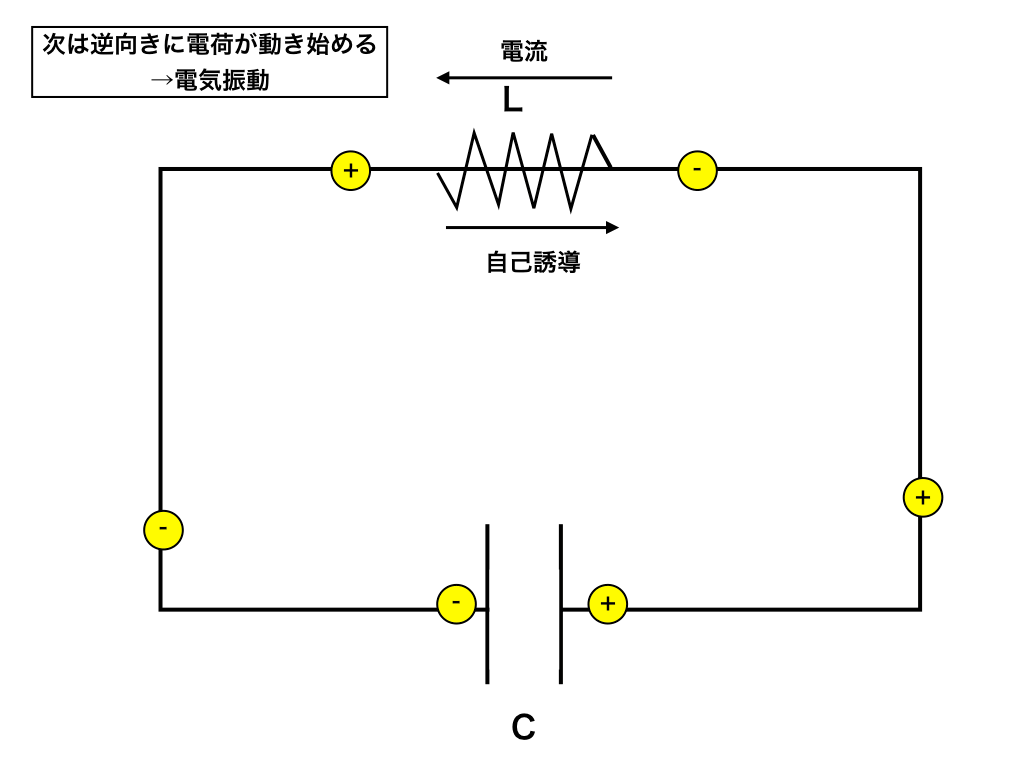
元の状態に戻る(そしてstep1・2へ)
また暫くすると、step0の状態になります。
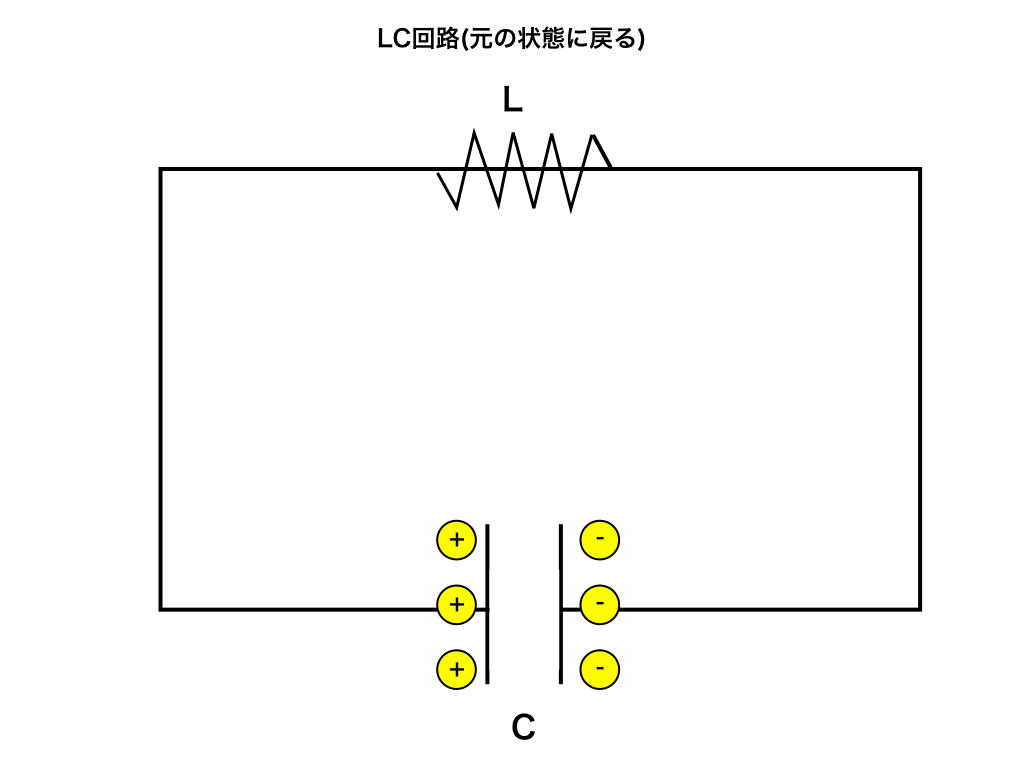
そして直ぐにstep1へ電荷が動き出します。・・・
この様子を【電気振動】と言います。
振動回路の持つエネルギー
”理想的”な回路(途中の電荷移動によるエネルギーの損失がない)場合、力学の単振動で学んだエネルギー保存則とソックリの「電気振動でのエネルギー保存則」が成り立ちます。
この式は問題を解く上で必須なので、必ず覚えておきましょう。(導き方はやや複雑な積分計算を伴うので、記事の最後に掲載しておきます。)
$$\frac{1}{2}LI^{2}=\frac{1}{2}CV^{2}$$
電気振動まとめと続編へ
今回は、RLC(直列)回路の『共振』と、LC回路での『電気振動』について紹介しました。
前回の記事がしっかりと理解出来ていれば、それほど難しい話ではない(はず・・・)なので、もしつまずいたところがあれば、何度か前の記事とこの記事を行き来して完全に理解する様にしましょう。
次回はここまでの交流の範囲(プラスα)から、より理解を深める為の【定着・演習問題編】を扱います。
関連記事一覧と問題編
交流回路第一回:「”RLC”直列回路と”インピーダンス”の求め方」
交流回路第二回:「(今ココです)共振とLC回路(電気振動)」
交流回路第三回:「(作成中です)交流回路の様々な問題【定着・演習編】」
>>「電磁気分野全体のまとめページ」<<
付録(電気振動とエネルギー保存の導出)
キルヒホッフの法則(電圧降下)を用いて、導出していきます。
まず、「コンデンサーの基本・公式・仕組み」より
Q=CV・・・(1)
コイルの\(V_{自己誘導}=-L\frac{di}{dt}\)・・・(2)
さらに、\(i=\frac{dq}{dt}\)・・・(3)
より、(1)と(2)から$$\frac{q}{C}=-L\frac{di}{dt}$$
(3)を両辺にかけると、$$\frac{q}{C}\frac{dq}{dt}=-Li\frac{di}{dt}$$
両辺にインテグラルをつけて、『tで積分』すると、$$\int \frac{q}{C}\frac{dq}{dt}dt=-\int Li\frac{di}{dt}dt$$この式を整理して、
\(\int \frac{q}{C}dq=-\int Li di\)
よって、$$\frac{1}{C}\frac{q^{2}}{2}+Const_{1}=-L\frac{i^{2}}{2}+Const_{2}$$
積分定数をまとめて移項し、q=CVを用いると
$$\frac{CV^{2}}{2}+L\frac{i^{2}}{2}=Const$$
よって『コンデンサーのエネルギー』と、『コイルのエネルギー』の和は一定である事が示せました。
最後までご覧いただきまして、有難うございました。
”スマホで学ぶ”『受験・学習メディア:「スマナビング!」』では、ご意見/ご感想/誤植の指摘などをコメント欄にて募集しています。
(※『個々の問題の解き方』等のご質問については、対応できない事がございます。ご了承ください)
・その他のお問い合わせ・ご依頼につきましては、引き続き受け付けております。
>>【運営元ページ】より、ご連絡をお願いします。

