
慣性力/束縛条件の解説と問題のpoint
これから”動く三角台”と”動滑車”の有名問題を使って、「慣性力」と「束縛条件」の利用の仕方を解説していきます。
目次(タップした所へ飛びます)
慣性力と束縛条件
・慣性力とは何か?
・慣性系と非慣性系
・束縛条件とは?
・有名問題を束縛条件を使って解く
次回
・同じ問題を慣性力を使って解く
慣性力とは何か?
そもそも、慣性力とはなんなのでしょうか。簡単に言えば「実際には存在しない見かけの力」です。
例えば、加速度aで動いている車の窓から、外に立っているBさん(静止している人:質量mとする)を見るとBさんはーaの加速度で運動(=逆向きに進んでいる)様に見えます。
この時の逆向き(に働いている様に見える)力「ma」の事を慣性力と言います。
慣性系と非慣性系
先ほどの例を使うと車中の人(Aさん)からは逆向きに運動している様に見えたBさんですが、Bさんの横にCさんが居るとすると、Cさんは当然Bさんが運動しているようには見えません。
この様に同じ観測対象(Bさん)でも観測する側が加速度運動しているか否かで見え方が違います。
束縛条件
束縛条件、若しくは拘束条件とも言われる条件があります。これは図形的(幾何的)な制限と言えます。
普段は意識していないのですが、難問になってくるとこの条件をもとに式を立てる必要が出てきます。
具体的には、この後の問題で紹介しますが、「三角台の上を滑り降りる物体」や「動滑車が絡む問題」で幾何的な制限(滑車であれば、糸の長さは不変、など)から立式する事が多いです。
未知数の個数が式の数より多ければ、連立方程式で解けないので、未知数の個数=式の数にする為に束縛条件を考えてみることが大切です。
今回は動く三角台とその上に乗せた物体の問題を通して、束縛条件の使い方を解説して行きます。
束縛条件で動く三角台問題を解く
<図1>の様に角度θの斜辺を持つ質量Mの三角台Sがある。
今三角台Sの上に質量mの物体Bを置くと三角台Sは左へ動き始め、物体Bは斜面を滑り降り始めた。
ただし重力加速度をgとし、地面と三角台Sおよび、三角台S と物体Bの間には摩擦力が働かないものとする。
(1)三角台Sの水平方向左向きを正として加速度Axを求めよ。
(2)物体Bの地面に対しての水平方向右向きを正とした加速度Bxを求めよ。
(3)物体Bの地面に対しての鉛直方向下向きを正とした加速度Byを求めよ。
ただし、物体BがSに与える垂直抗力をNとして使って良い。
(4)上記の垂直抗力Nを本文中の文字を使って表せ
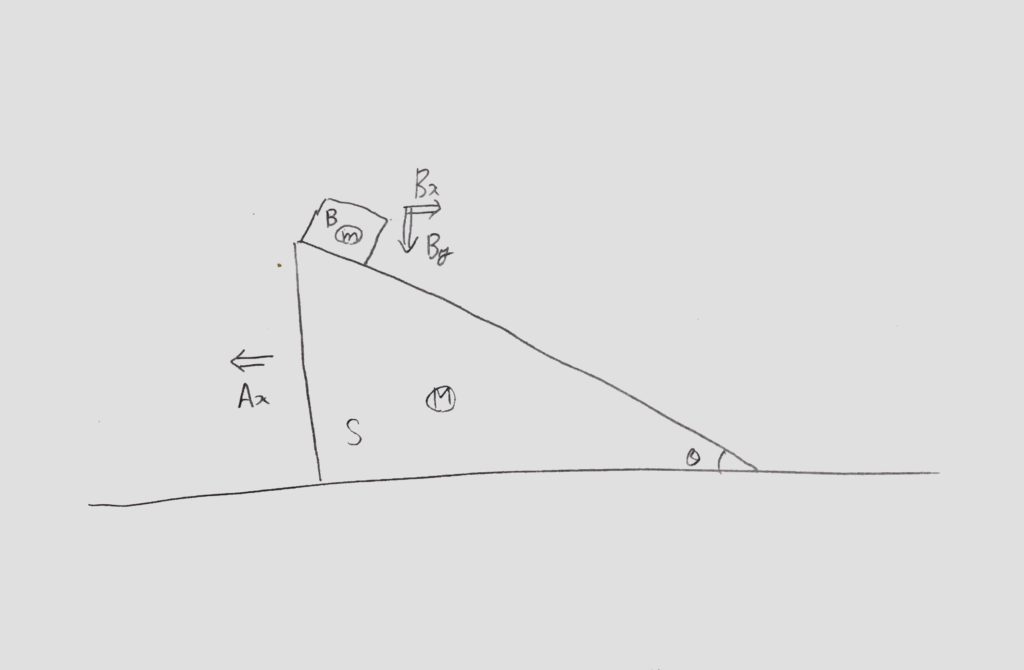
<図1>
力学の問題の鉄則として、
「先ず第一に軸を設定し、その正負の方向を決める」
↓
「次にかかる力や加速度を図に書き込んでいく」
↓
「それをもとに運動方程式やつりあいの式を立てる」
という流れがあります。今回もそれに従っていきます。
解答解説編
(1)今回は問題文に正方向が指定されているので、それに従います。
かかる力を書き込んで、
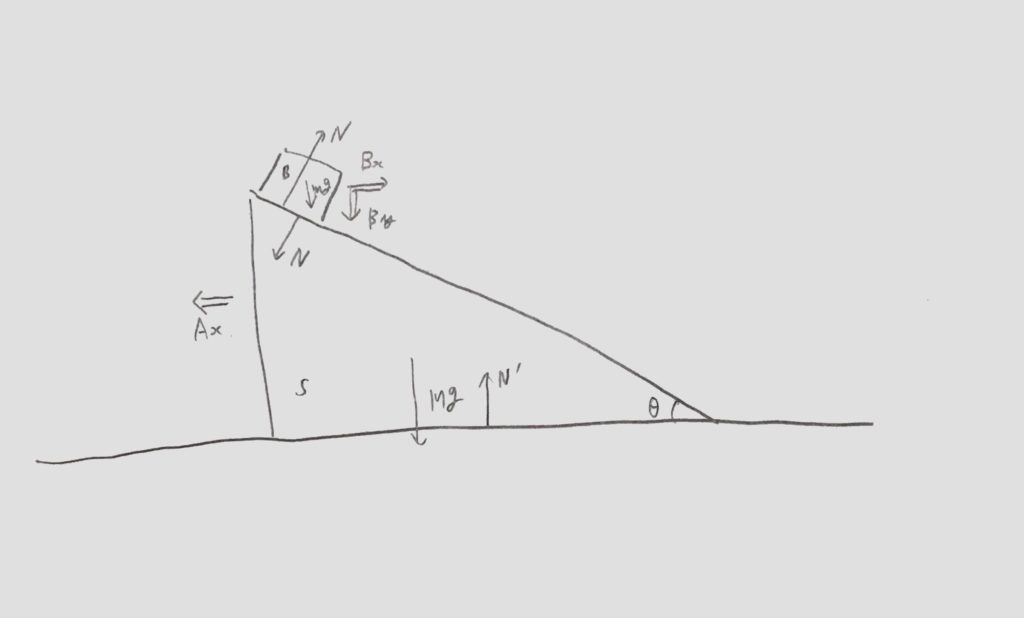
またNを使って良いので三角台Sの運動方程式は
MAx=N sinθ
∴ Ax=Nsinθ/M
また物体Bには、作用反作用の法則よりNが斜面に垂直上向きにかかるので、運動方程式を立てて解くと、
(2)
mBx=N sinθ
∴ Bx=Nsinθ/m
(3)
mBy=mgーN cosθ
∴By=gーNcosθ/m
ここまではスムーズにこれると思います。
問題は次の問4です。
(4)Nをm、M、θ、g(全て問題文中で与えられた文字)で表す必要があります。
今、未知数はAx、Bx、By、Nの4つ。
対して、式の数は(1)〜(3)の運動方程式三つ。
ここで束縛条件が必要になります。
以前「波の方程式の作り方講座:二枚のグラフを活用する方法」でも、
・「迷ったら少し時間が経った状態へずらす」
というテクニックを紹介しましたが、今回も同じ様に考えて、三角台と物体が少しの時間(t秒)経過した後の状態を描きます。
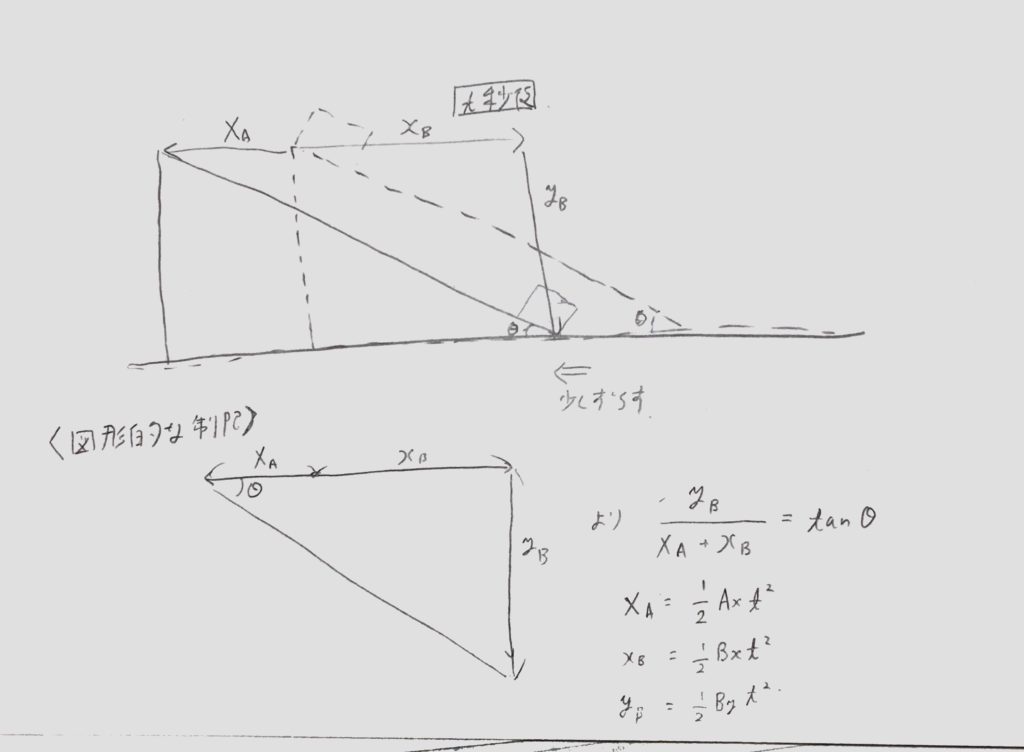
<図2>
すると<図2>の様にθよりも急角度で物体Bが滑り降りている様に見えます。
束縛条件は図形的な制限(物体Bは三角台S上を必ず動く)を式にするので、今<図2>でのそれぞれの移動距離をX a、xb、ybとして計算してみます。
すると<図2-下左>の様な三角形が出来るので、移動距離の束縛条件は<図2ー下右>。
ここで必要なのは加速度の関係式なので、
(1/2)t ^2でX A、xb、ybをそれぞれ割ると、
By=(Ax+Bx)tanθ、の式(束縛条件の式)が得られます。
これで未知数の個数=式の個数となったので、後は4式の連立方程式を解いていくだけです。
By=(Ax+Bx)tanθの式に、(1)〜(3)で求めたAx、Bx、By、を代入します。
$$g-\frac{N\cosθ}{m}=\tanθ(\frac{N\sinθ}{M}+\frac{N\sinθ}{m})$$
代入した式をN=の形に変形していきます。
$$\frac{g}{\tanθ}=\frac{N\sinθ(m+M)}{Mm}+\frac{N\cos^{2}θ}{m\sinθ}$$
$$Mmg\cosθ=N(m\sin^{2}θ+M\sin^{2}θ+M\cos^{2}θ)$$
$$Mmg\cosθ=N(M+m\sin^{2}θ)$$
よって、
$$N=\frac {Mmg\cosθ}{M+m\sin^{2}θ}$$
・・・(4)の答
小まとめ
この問題のポイントは、問4で三角台の上を物体Bが滑り降りるところから、t秒後にずらし、移動距離から加速度の関係式を導く(=束縛条件の式を導く)ところです。
これは一度経験しておかないと自分で思い付くのは苦しいので、是非もう一回自力で解いて身に付けておいてください!
次回は、この問題を慣性力を使って解く方法を記事にします。
滑車と束縛条件の頻出問題
(*)記事のリクエストをいただいたので、『滑車』の問題について追加します。
滑車と3つの重りの問題
まずは問題図を見てみます。
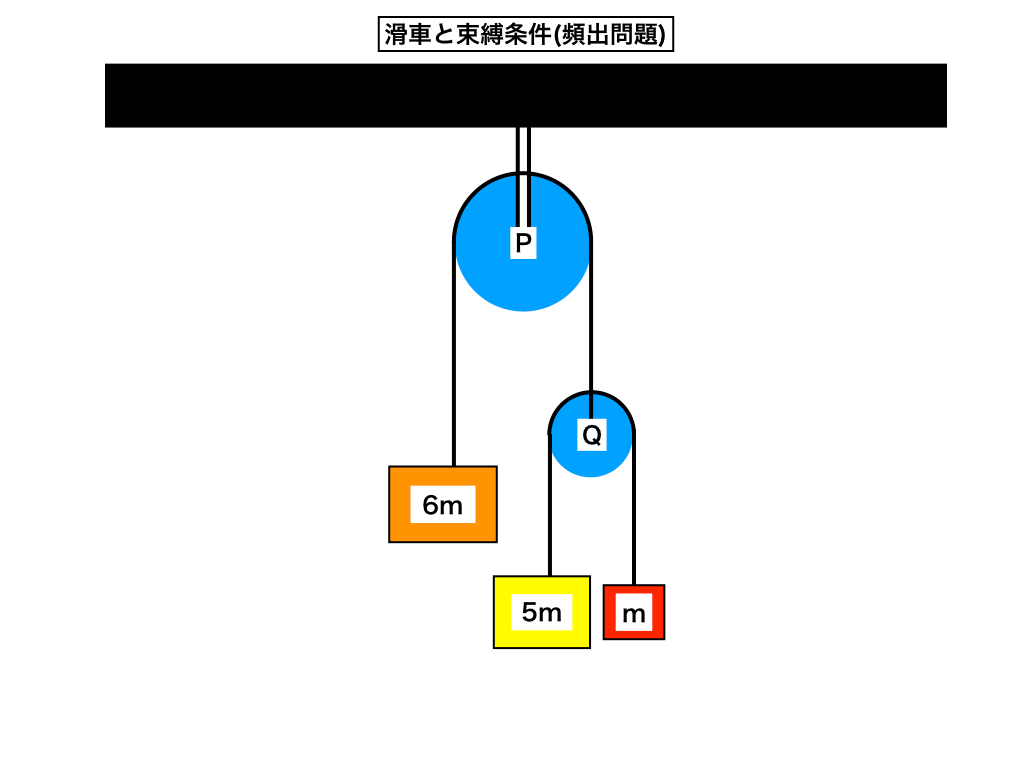
上の図のように、定滑車Pにオレンジの6mの重りと動滑車Qをつり下げる。さらに、Qの片側には黄色の5mの重り、もう片方には赤色のmの重りをそれぞれつり下げている。
重力加速度をgとし、『それぞれの糸の長さが変化せず』、『糸、滑車P・Qの重さを0』として考えるとき、3つの重りの加速度と2つの糸にはたらく張力2つを求めよ。
よくある誤解と解答解説編
この類の問題で頻繁に見られる誤答は、下図のように
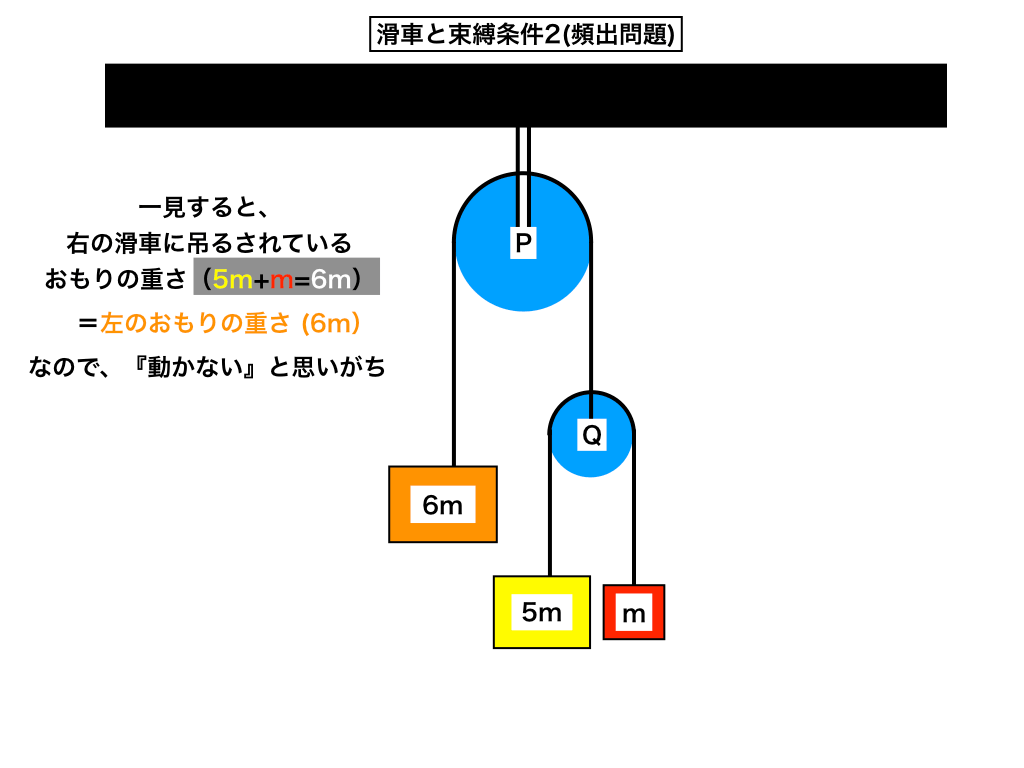
「Pの左右の重りが同じなので滑車が動かない」というものです。しかし、実際にはQの滑車につり下げた黄色と赤色の重りが運動するため、滑車Q,オレンジの重りとも運動します。
では実際に解いていくことにしましょう。
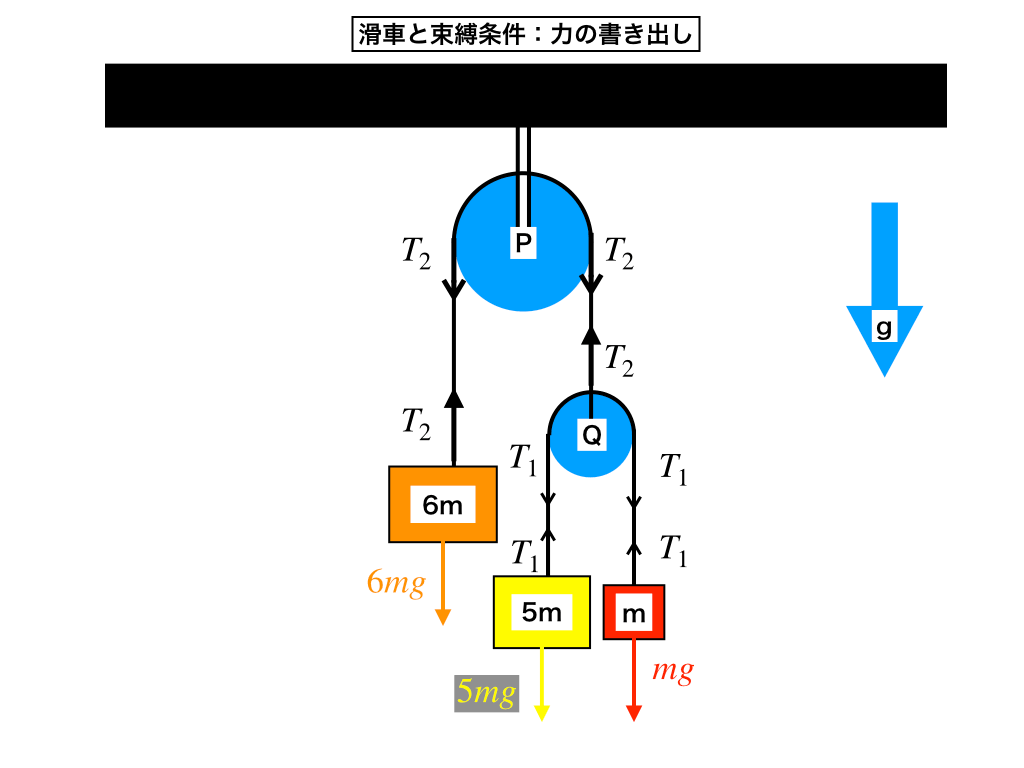
それぞれの力の矢印を『下向きを正として』書き出した上で、運動方程式を作っていきます。
力の矢印と立式
赤のおもりの加速度を"a"、黄色の〃加速度を"b"、オレンジの〃加速度を”c”として、張力をT1,T2とします。
赤:ma=mg-T1・・・(1)
黄:5mb=5mg-T1・・・(2)
オレンジ:6mc=6mg-T2・・・(3)
さらに、滑車Pは:0m・c=2T1-T2・・・(4)
式が4つ、未知数が(a,b,c,T1,T2)の5つなのでこの場合も何らかの拘束(束縛)条件が必要となります。
そこで、『糸の長さが一定』=『糸がたゆまない』=『糸の両方の”加速度の大きさ”が同じ(端がそれぞれ違う加速度で運動すると、糸が切れたりゆるんだりしてしまう為)』を使います。
糸の長さが一定
滑車Qの上からそれぞれの加速度を見ると、上記の拘束条件より「c+a=(-1)(c+b)」・・・(5):『cで運動するQから見た、赤色の加速度aは:(c+a)。これと反対向きの加速度:(c+b)が等しい』という事を立式しました。
これで、未知数5つ、式5つとなって連立させて解くことが出来るようになりました。
ゆえに、(1)から(5)を連立して計算すると、
$$a=-\frac{8g}{7}、b=\frac{4g}{7}、c=\frac{2g}{7}$$
$$T_{1}=\frac{15mg}{7}$$
$$T_{2}=\frac{30mg}{7}$$
がそれぞれ求まります。
(注)下向きを正と設定したので、上向きに加速度運動する赤のおもりの符号は”ー”となっています。
力学の解説記事へ
記事のリクエスト、お問い合わせはコメント欄よりお願いします。

