気柱の振動の問題(開/閉管)と開口端補正(物理:波動)
<この記事の内容>:物理の波動分野のうち、『縦波である音波』と”気柱の振動”について0から解説しています。
<関係が深い記事>:「弦の振動と線密度・波を伝わる速さのまとめ」
目次(タップした所へ飛びます)
気柱の振動
音波の中でも、のちに紹介する【ドップラー効果】の次に頻出と言える「気柱の振動」。
以下のイラストの様に、
・管の片側が閉じている「閉管」や
・両側ともに開いている「開管」に向けて、スピーカーから音を出した時に起こる『共鳴』の条件などから、
・「音速:v(m/s)」や、
・「定常波の波長:λ(m)」、
・「開口端補正の長さ:(m)」などを問われます。
波長λと腹・節
これから頻繁に出てくる、「入射波と反射波」によってできる定常波を簡単に見ておきます。
一個のラグビーボールのような、節→腹→節までが\(\frac{\lambda}{2}\)で、これが2つ繋がることでλとなります。
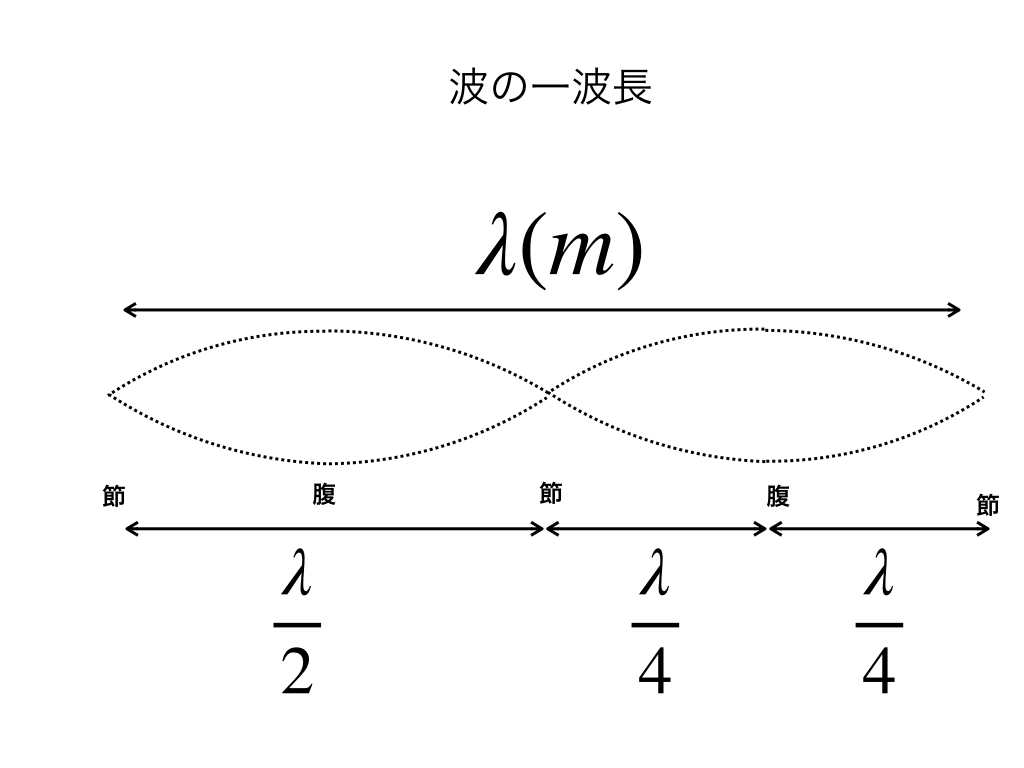
<λのイメージ>
閉管:片方のみ空いている場合
さて、閉管に向けて音を出すと閉じている側で「固定端反射」が起き、その位置が定常波の節になります。
閉管の仕組みと固定端反射
また、開いている方が腹となります。
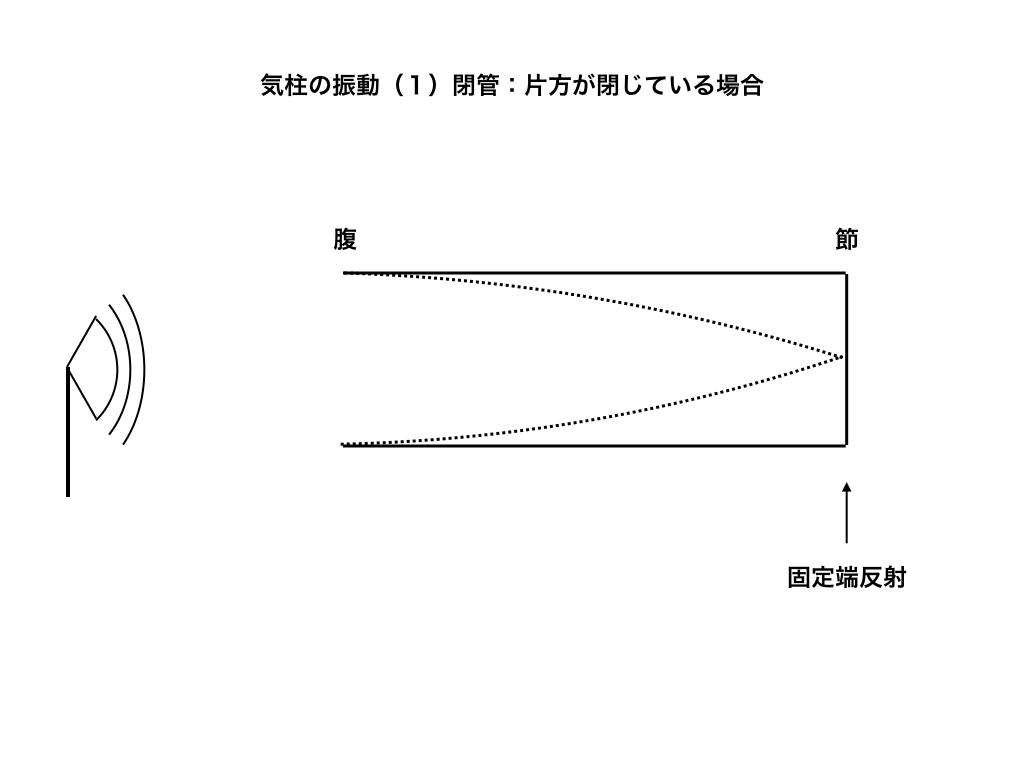
<閉管とその基本振動のイメージ>
基本振動/3倍振動/(2n-1)倍振動の意味と図
この様な閉管では、常に片方の端が固定端反射によって節となり、開いている方が腹となるので
・【1/4λ=閉管の長さ】のとき基本振動となり、その3倍・5倍・7倍・・・と奇数倍(2n-1)倍の振動を起こした時に共鳴を起こします。(閉管の長さを変化させたり、\(v=f\lambda\)より、音源の周波数を変えた時など)
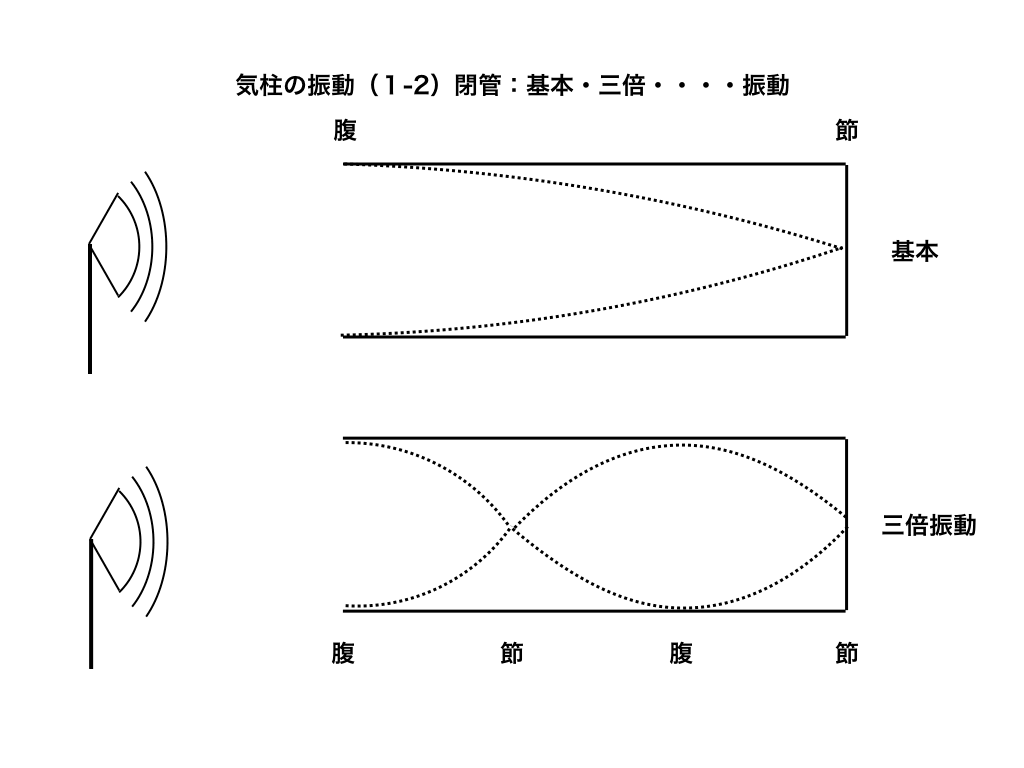
<閉管と”奇数”倍の振動のイメージ>
開管:両端が開いている場合
今度は両方の端が開いている「開管」についてみていきます。
開管と自由端反射
開管の場合は、管の両端で自由端反射が起こって腹となります。
また、閉管の時のように条件を変えていくと、基本・二倍・三倍振動・・・と基本振動とその自然数倍の時、共鳴が起こります。

<開管と”n倍”振動のイメージ>
開口端補正の意味と計算
次は苦手な人が多い、「開口端補正」についてみて見ましょう。
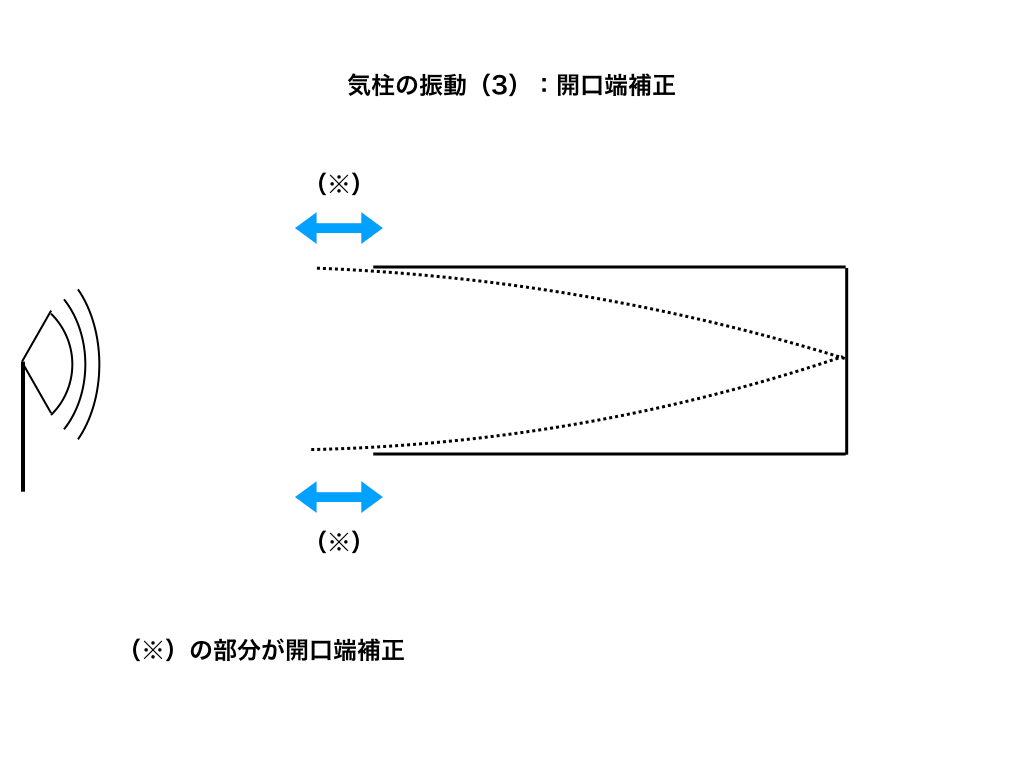
<開口端補正のイメージ>
このように、少しだけ波が開いている方の端(=開口端)から飛び出している場合があり、これを「開口端補正」と呼びます。
この(※)の長さ(m)を求めさせる問題はよく出ます。
が、基本振動でも3倍振動でも、『開口端補正の長さは同じ』である、という事を利用して計算していきます。(詳しくは下の定着問題の(二)をご覧ください。)
定着用問題
ここでは、基礎的な問題を使って今回の内容の定着・確認と、実際にどういった問題が出されるのかについて解説付きで紹介します。
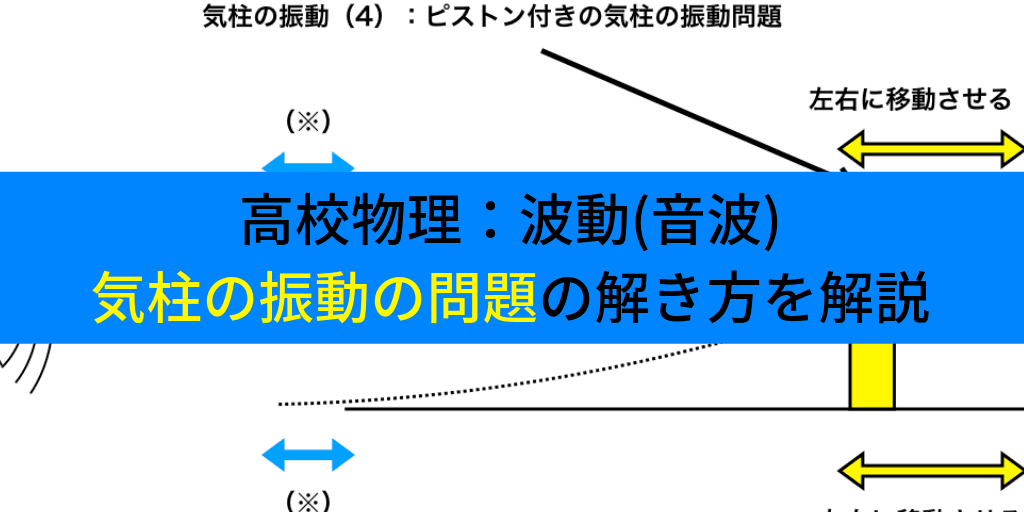
ピストンがついた(閉管)気柱の振動問題
さっそく今回の締めくくりとして、気柱の振動でも特に頻出である【閉管の固定端の部分にピストンを取り付けて、これを動かす】ときの問題を解いていきましょう。
問題:以下の図のように、スピーカーとその右側にピストンによって長さが自由に変更できる管がある。
今ピストンの栓から管の端までの距離を\(x_{◯}\)とすると、\(x_{1}=0.11(m)\)の時基本振動がおき、次に共鳴を起こしたのは、\(x_{2}=0.49(m)\)の時であった。
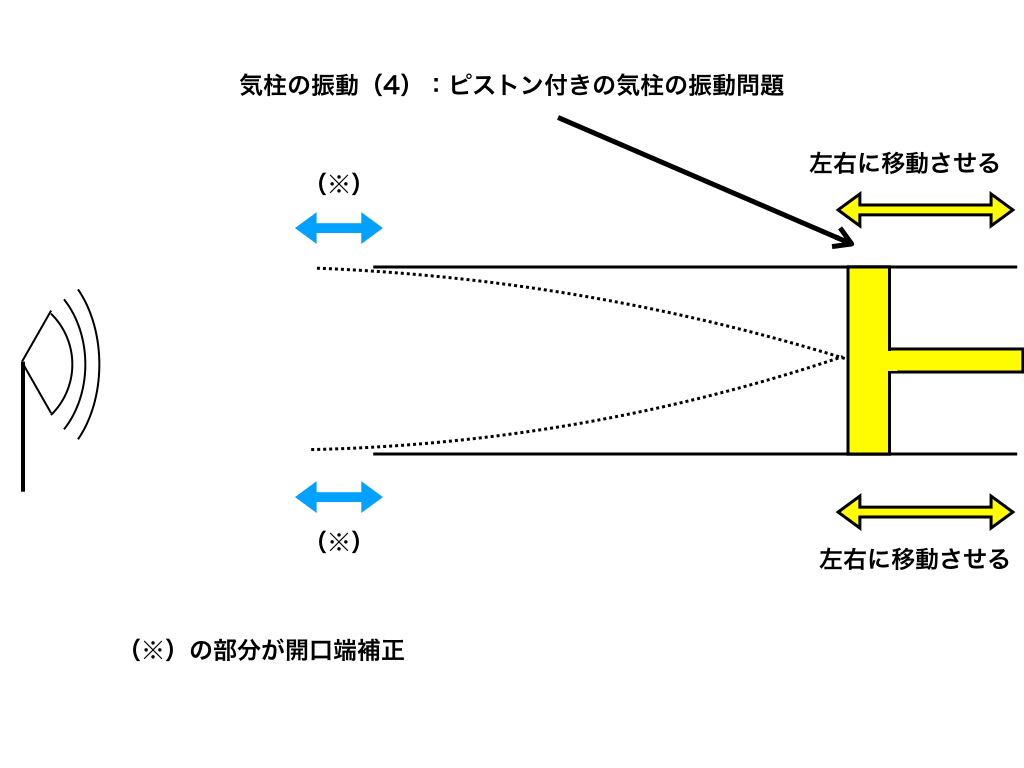
このとき、次の問題を解け。ただし、\(音速V_{s}=334(m/s)\)とする。
(1)音波の波長λ(m)を求めよ。
(2)開口端補正(図中の※)の距離をΔL(m)とする。この値は何mとなるか。
(3)スピーカーから発せられている音波の周波数f(Hz)の値を求めよ。
解説
ではそれぞれの問の解説に入ります。
はじめは、特に【開口端補正】の扱いで悩むことがありますが、どれも典型問題なので必ず解ける様にしておきましょう。
波長を求める
(1)波長は、条件で与えられている『三倍振動\(x_{2}+\Delta L\)=ラグビーボール3/2個分\(\frac{3\lambda}{4}=0.49(m)\)』と『基本振動=\(x_{1}+\Delta L\)=〃1/2個分\(\frac{\lambda}{4}=0.11(m)\)』の2つから計算します。
先ほども少し書きましたが、何倍振動であっても開口端補正:ΔLの長さは同じであることから、
$$x_{2}+\Delta L-(x_{1}+\Delta L)=\frac{3\lambda}{4}-\frac{\lambda}{4}$$
(これで綺麗にΔLが消えてくれます)
よって、$$\lambda=(0.49-0.11)\times 2=0.76(m)・・・(答)$$
開口端補正を求める
次に、波長が求まったので、$$x_{1}+\Delta L= \frac{\lambda}{4}$$のλに代入すると、ΔLは簡単に求まります。したがって、\(0.11+ΔL=0.76\times\frac{1}{4}\)
ゆえに、開口端補正:ΔL=0.08(m)・・・(答)
周波数を求める(公式の復習)
最後の(3)は、波の分野で最も重要な『v=fλ』を覚えているかを問うだけの問題です。
ここでのvは音速V_{s}、λは既に求まっているので、\(V_{s}=f\times \lambda \)にそれぞれ代入して、
\(334=f \times 0.76 \leftrightarrow f≒439.4\)
したがって、音波の周波数fは440(Hz)・・・(答)
記事のまとめと波動(音波)の関連記事へ
気柱の振動は、今回の定着問題レベルであればセンター(共通テスト)のレベル〜出題され、これを他分野と融合させて難易度を上げた問題は難関大学でもよく出題されます。
よく復習して、基礎が身についたら融合問題にチャレンジしてみて下さい!
次回は「おんさと弦の振動・線密度の公式を具体的な問題で解説!」について扱います。
関係する記事(ドップラー効果など)
音波での出題率No. 1のドップラー効果を合わせて読んで起きましょう!
「反射板・音源・観測者がそれぞれ動く場合や風が吹いている場合(応用編)」
「斜め方向のドップラー効果と上空を飛ぶ飛行機の問題(演習問題編)」
今回も最後までご覧いただき、ありがとうございました。
「スマナビング!」では、読者の皆さんのご意見・ご感想などの募集をコメント欄で行なっています。
また、お役に立ちましたら、snsでB!やシェアをしていただけると助かります。
・お問い合わせ/ご依頼/その他ご連絡は、【運営元ページ】よりお願いいたします。

