高校物理と化学が繋がる!原子物理第4回
#2018/11/26更新しました
今回は前回(ド・ブロイ波とボーアの量子条件、水素原子の軌道半径)の続きです。
前回を未読の方は先に第3回を読んでいただけるとスムーズに理解が進むと思います。
原子物理シリーズ
第1回:「光電効果とは?」
第2回:「コンプトン効果がわかる」
第3回:「ド・ブロイ波とボーアの量子条件」
目次(タップした所へ飛びます)
水素原子のエネルギー準位から特有の線スペクトルしか出さない理由が明らかに!
化学で習うイオン化エネルギーの正体も分かる!
(また、既読の方も第四回を読み終わったら第三回を読み直して、行ったり来たりを繰り返しながら復習して下さい)
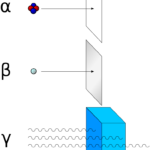
さて、水素原子は普通の光源と違い非連続な線スペクトルしか出さないのでした。
その理由を早速解明しましょう。
前回述べたように、水素原子の電子軌道半径はボーアの量子条件とクーロン力を向心力とする
等速円運動の式より
$$r( n) =\frac {h^{2}n^{2}}{4\pi ^{2}kme^{2}}$$
r(n)=h2n2/4π2kme2 ・・・#1と表せました。
n=1,2,3,,,となるに連れて我々の知っているK殻L殻・・・に対応するのでしたね。
ではいきなりですが、太陽と地球をイメージしてみてください。
地球は太陽の周りを回っています。
そして、太陽が動いていないとすると地球は猛スピードで運動しているのでエネルギーを持っていますね
運動エネルギーと万有引力による位置エネルギーです。
これとほぼ同じようなことが原子でも言えます。
つまり太陽が原子核、地球が電子の役割です。そして地球のエネルギーの代わりに
電子の運動エネルギー&クーロン力による位置エネルギーに置き換えられます。
原子半径r(n)上の電子のエネルギーの和を水素原子のエネルギー準位と言い、
E(n)で表します。(nは勿論1、2、3、、、K殻L殻M殻・・・に対応しています)
$$E_{n}=\frac {mv^{2}}{2}+( -\frac {ke^{2}}{r}) $$
E(n)=(mv2)/2 +{-ke2/r}となります。・・・#2
※クーロン力に取る位置エネルギーがマイナスな理由は、無限遠を基準にしている為です。






さて、#1の式のvを等速円運動とクーロン力の式で消去して、r(n)に#2を代入します。
$$すると、E_{n}=-\frac {2\pi ^{2}k^{2}me^{4}}{h^{2}n^{2}}$$
En=-2π2k2me4/h2n2 ・・・#3になります。
nの数が大きいほど軌道半径は大きくなるので、原子核から離れていきます。
そしてここからが最重要です。
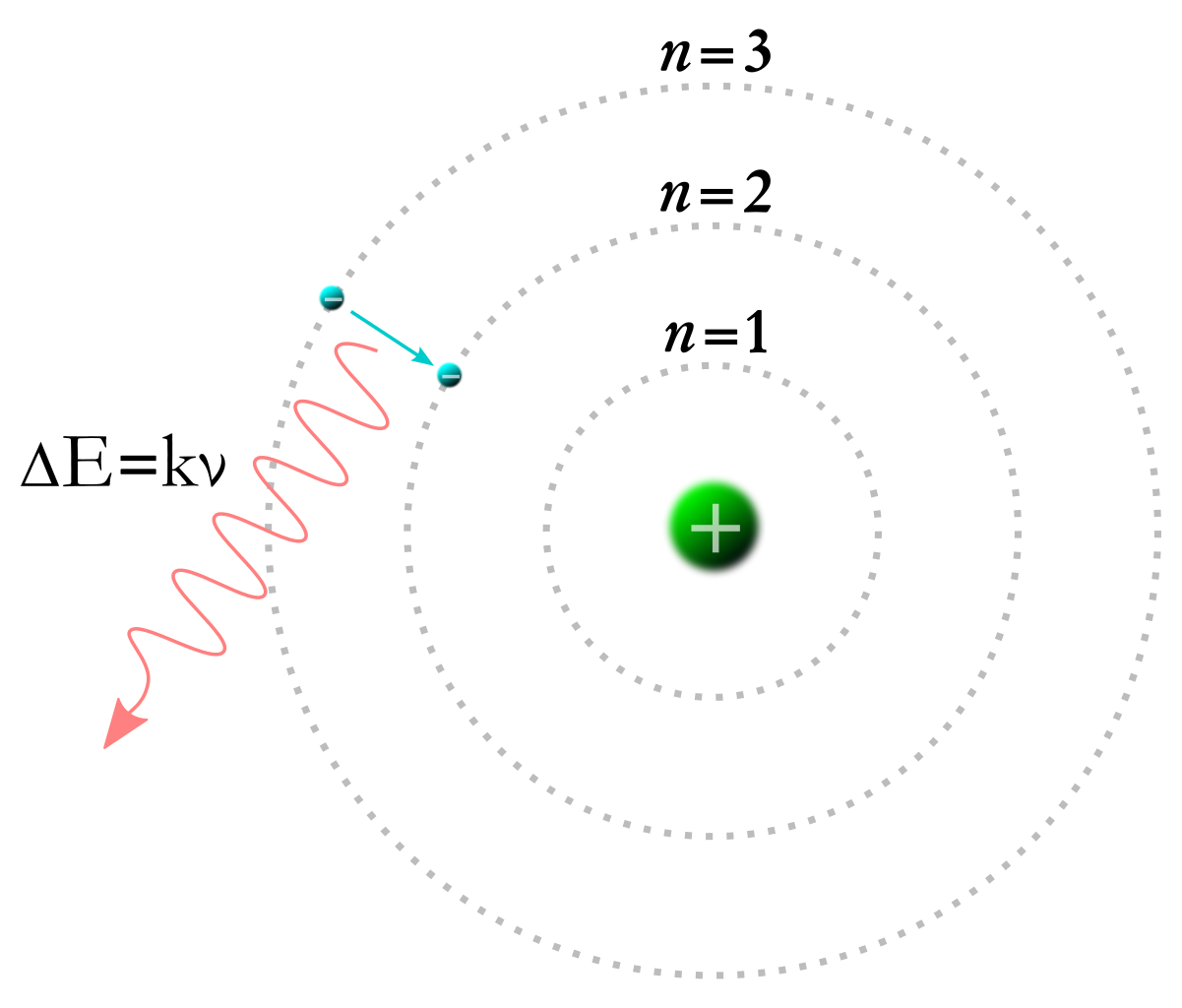
外側の軌道から電子が内側に落ちるとき、エネルギー準位はマイナスが大きくなるので、その差の分のエネルギーを光子として放出します。
<図1>参照
その式は、E highーE low=hν=hc/λと表せます。
<図1>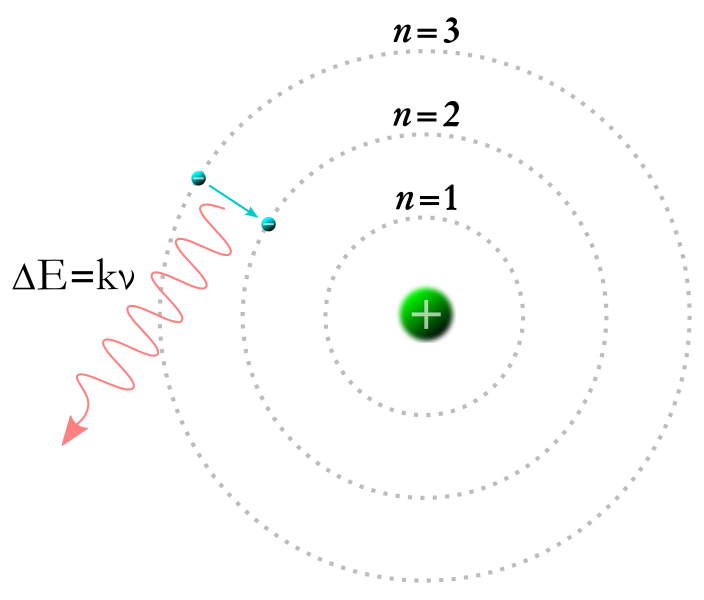
落ちた先の軌道のnの値によって
1の時、ライマン系列
2の時、バルマー系列
3の時、パッシェン系列と言います。
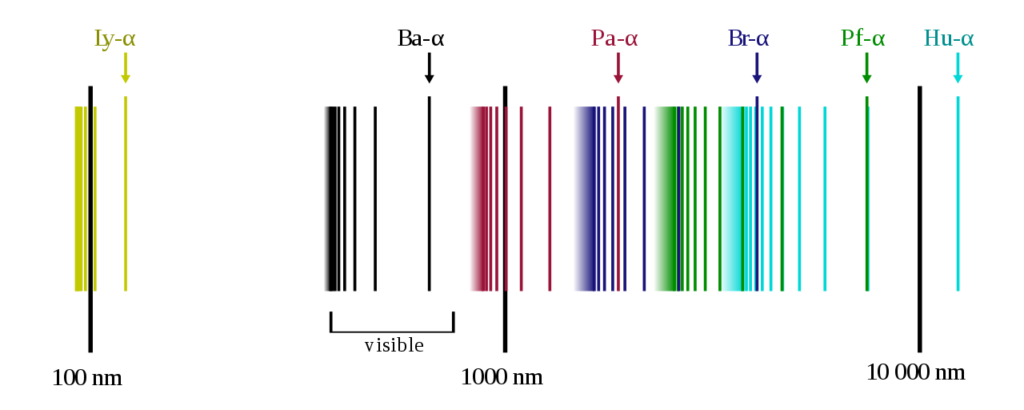
(図2参照)
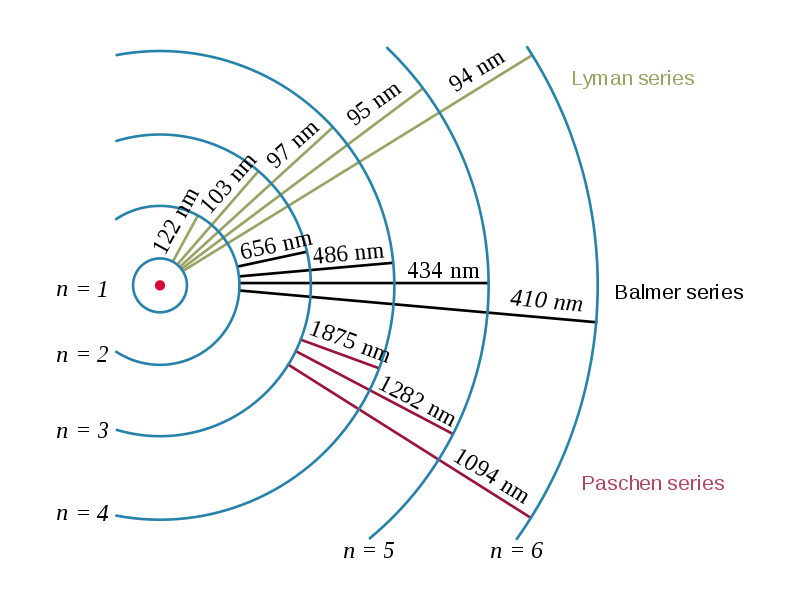
image by OrangeDog <図2>
そして、どの軌道からであろうと、落下した先の系列で分類し、ライマン系列はn=1なので一番原子核に近く次にバルマー、パッシェンとなります。
ライマン系列は一番エネルギー準位が低いので、ここへ電子が落下した時は一番大きなエネルギーが放出されます。
ここで、E highーE low=hν=hc/λの式を思いだすと、
大きなエネルギー放出=hc/λの数字が大。
よってプランク定数と光速は変わらないので、波長λが小さい=振動数νが大きいことから
ライマン系列行きは、波長の短い紫外線を放出します。
バルマー系列行きは、その次に波長が短い、可視光線を放出します。
ライマン系列行きは、もう分かりますか?赤外線を放出します。
さて、これで水素原子が飛び飛びの波長の光(特有の線スペクトルしか出さない)理由がわかります
第4回のラストテーマです。
高校化学〜イオン化エネルギー〜と高校原子物理の融合!
ここで、En=-2π2k2me4/h2n2 ・・・#3 より、
n=∞の時のEnは0、
$$\begin{aligned}E_{n}=-\frac {2\pi ^{2}k^{2}me^{4}}{h^{2}n^{2}}\\
n\rightarrow \infty ,E_{n}\rightarrow 0\end{aligned}$$
n=1の時のEnは#3より、
E1=ー2π2k2me4/h2
したがって、イオン化エネルギーの値は
I=0-(-π2k2me4/h2)
$$I=0-( -\frac {π^{2}k^{2}me^{4}}{h^{2}× 1^{2}}) $$
よって、I=2π2k2me4/h2
$$I=\frac {2π^{2}k^{2}me^{4}}{h^{2}}$$
と表せました。
どうでしたか?かなり計算は複雑ですが、考え方自体は単純です。
ただ慣れないと難しく感じてしまう分野なので、自分で手を動かして、自動的に公式が書けるようになるまで、練習してみて下さい。
また、第三回の記事も繰り返し読んでおいて下さい(3、4回はセットなので)
原子物理第五回はX線や、ブラッグ反射を行います。お楽しみに!(製作中です)
ではお疲れ様でした(^ ^)
教養として、原子物理関連の記事を作成しました。
お役に立ちましたら、はてなブックマークや、公式Twitterのフォローをぜひお願い致します。