image by Trassiorf
ベクトルの終点の存在範囲
この記事では、「ベクトルの終点の存在範囲」の問題が苦手な人or初めて学習する人を対象に、苦手となる3つの原因を取り除き、基本的な存在範囲の問題が解けるところまで解説しています。
※2025/04/20更新:続編作成しました!(続編では、この内容を応用し、存在範囲が領域になる場合やその面積を求める問題の解き方を紹介しています。記事の下のリンクからご覧いただけます。)
また,斜交座標の考え方のページも作成予定です。
目次(タップした所へ飛びます)
ベクトルの終点の存在範囲が苦手な原因3つとそれぞれの対処法
・(1)ベクトルそのものが苦手な人とその対処法
・(2)「係数和1」の理解があやふやな場合とその対処法 ”何よりも先に「係数和1をマスター!」”
・(3)単にこの単元の解法が良くわからない場合の解説(本記事のテーマはコレです)
この「終点の存在範囲」の単元もイマイチよく理解出来ずに、苦手になってしまう人が多いです。
(そもそもベクトル自体が苦手という人が多いという事実があります、、、)
(1)ベクトルそのものが苦手な人
ベクトルそのものが苦手な人は、「スカラー量(これまでの数学・算数で扱っていた数)に慣れていたのに、突然ベクトル量(向きと大きさという2つの情報を持った数)が出てきて戸惑っている」
場合があります。その様な人は先にベクトル入門第一回の記事を読んで見て下さい。
(2)ベクトルの概念は分かっているが、「係数和1の法則」がしっかりと身に付いていない場合
もし、「三角形OABにおいて、AB上に点Pをとる。この時OP=OA+OB のOAとOBの係数の和が1である理由」
を聞かれた時に即答出来なければ、この記事よりも先に下の記事を読んで下さい。
(それくらい、ベクトルのあらゆる問題で使用する超重要法則・条件です)
・(3)上2つはクリアーしたが、終点の存在範囲の問題が苦手な人は、
この下の2ステップで存在範囲の問題を解く方法を読んで下さい。
ベクトルの終点の存在範囲の問題を解く2ステップ
「係数和1」はしっかり理解できましたでしょうか。
では本題です。
終点の存在範囲の問題は色々ありますが、基本的に解く手順は決まっています。
実際に例題とともに習得していきます。
(問)、三角形OABにおいて$$\vec {OP}=s\vec {OA}+t\vec {OB}$$となる点Pをさだめる。
係数s,tが次の様な条件を満たして動く時の終点の存在範囲を表せ。
条件:2s+3t=4,s≧0,t≧0
(スマートフォン等でご覧の方で、数式の右端がはみ出してしまっている場合は横に傾けて頂くと見えます。現在修正中)
手順一:係数和1の法則を思い出して、何とか条件式(不等式or等式)の数字の部分を1にせよ!
Q,何故、数字の部分を1にするのか?
Ans,係数和1の法則のカタチに似せる様にする為です。
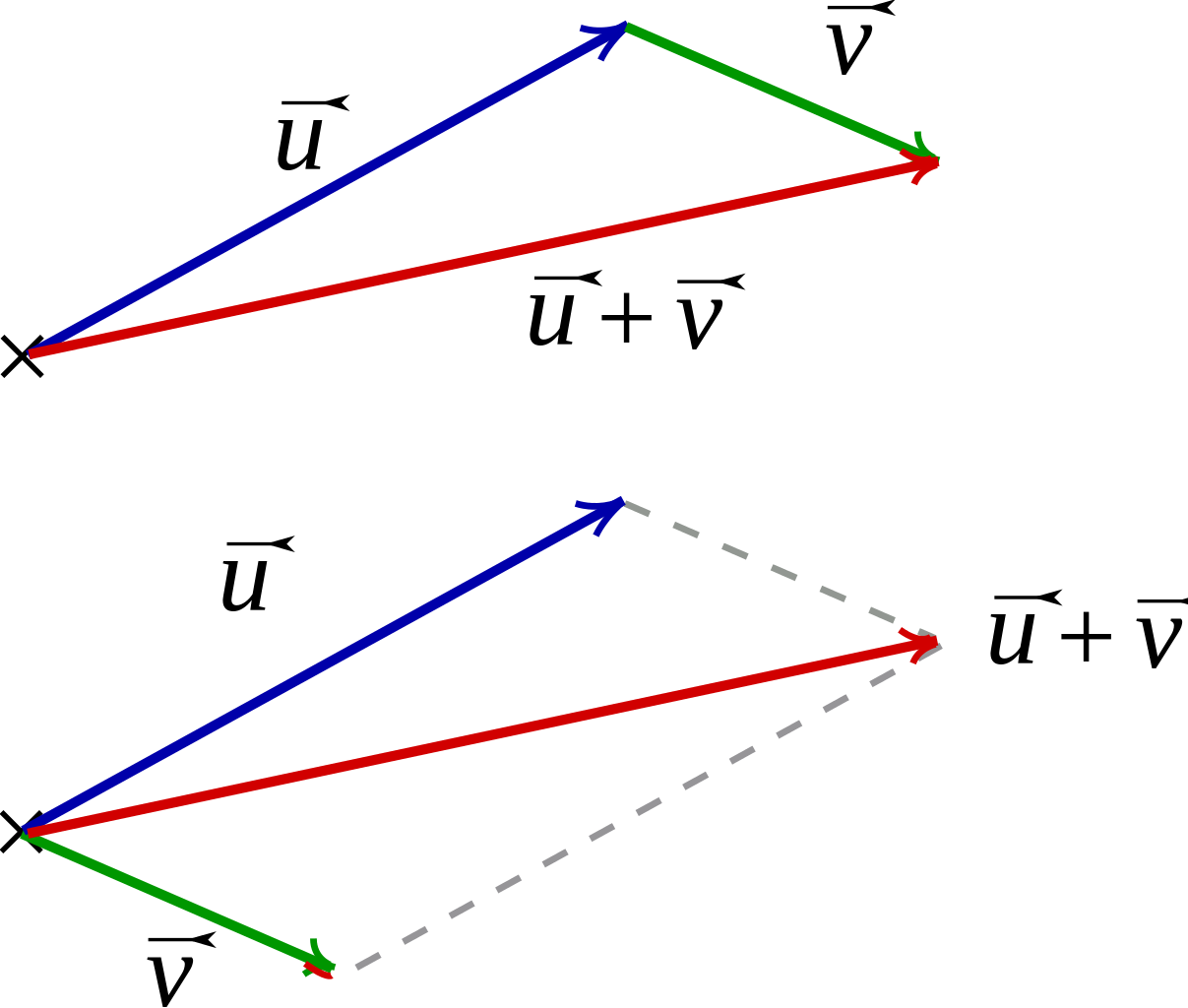
そうすれば法則『OP=uOA+vOB (u+v=1)の時、PはAB上にある』から、
ベクトルの終点を動く線分or直線が求められるからです
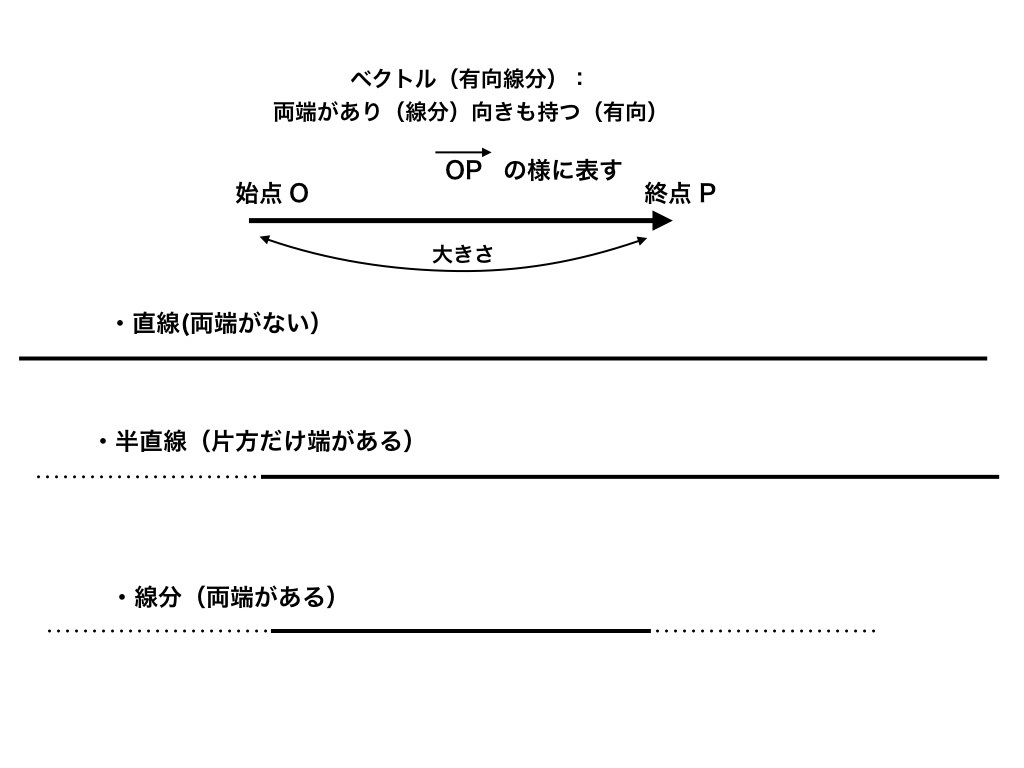
線分と直線の違い
※線分と直線の違いはしっかり理解できていますか?
また、半直線と直線、有向線分などこの辺りの用語が怪しい人は
→ベクトル入門第1回で詳しく解説しています。
<線分・直線・有向線分などの違いの図>
今回の場合は、『2s+3t=4』の”4”の部分を”1”にするために両辺を4で割ります。
すると、”係数の和が1”のカタチに近づきます。
$$\begin{aligned}\frac {s}{2}+\frac {3t}{4}=1\end{aligned}・・・#1$$
手順二:各ベクトルの係数で帳尻を合わせよ!
手順1では係数和1の法則に近付ける為に、むりやり数字の部分を1にしました。
勝手に4で割ってしまったので、それを調整するために以下の様にベクトルの係数部分を変化させます。
$$\overrightarrow {OP}=s\overrightarrow {OA}+t\overrightarrow {OB}=\frac {s}{2}× 2\overrightarrow {OA}+\frac {3}{4}t× \frac {4}{3}\overrightarrow {OB}$$
ここで、$$\frac {s}{2}=s',\frac {3t}{4}=t'とおくと#1よりs'+t'=1 。更に\\$$
$$\begin{aligned}2\vec {OA}=\vec {OA'}\\
\frac {4}{3}\vec {OB}=\vec {OB'}\end{aligned}とおく$$
$$\begin{aligned}\vec {OP}=s'\vec {OA'}+t'\vec {OB'}\\
( s'+t'=1) \end{aligned}$$
従って、点P はOAを2倍した点(A‘とおく)から、OBを4/3倍した点(B’とおく)まで動く線上にある。
s≧0、t≧0より、元々の式の係数がマイナスになることが無い(つまり外分しない)ので、
点Pは点A‘から点B’までの点より、題意を満たすものは線分A‘B‘である。
参考までに、答えの線分を図1に示しました。
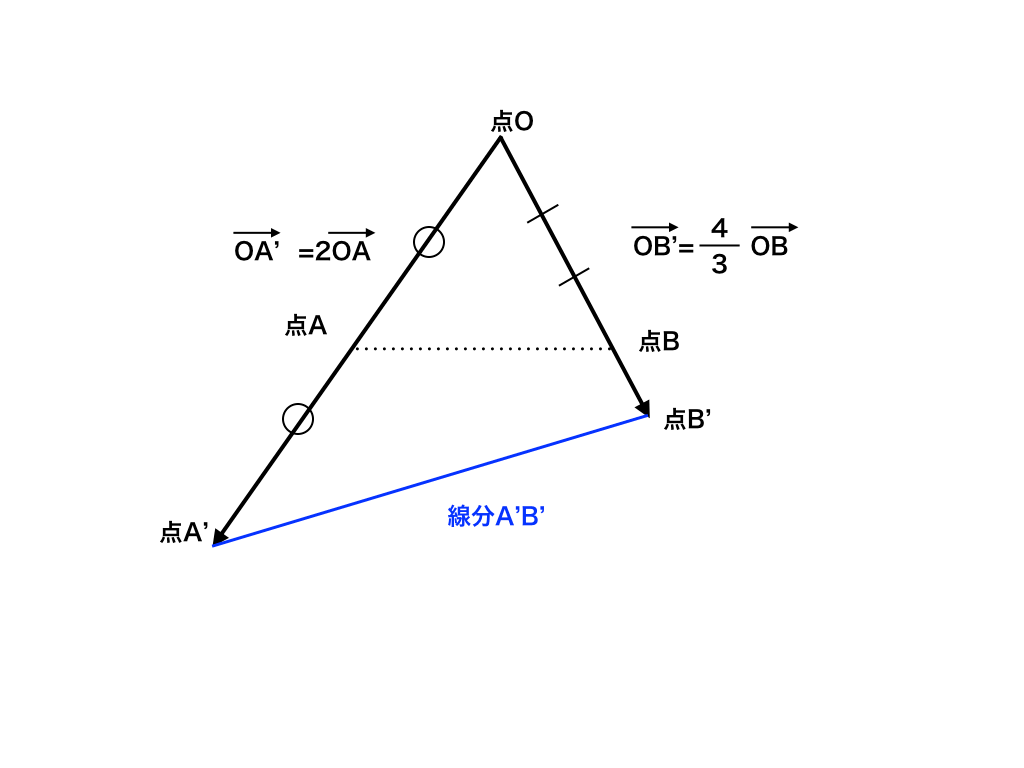
<図1:終点の存在範囲が線分A’B'>
まとめと存在範囲が領域になる続編記事へ(new!)
終点の存在範囲は、条件式の違いであと数パターン(線分や直線だけでなく、面積を求めるタイプなど)あります。
第二回では、=1のするために数字ではなく文字:Kで割って解く方法を使っていますが、
(係数の和を1にする)という基本的な考え方は今回と同じです。
残りのタイプについては記事が出来次第アップします。(2019/01/03続編出来↓)
>>「終点の存在範囲第二回:条件式が不等式になる場合の図示と求積問題」<<
ベクトルの総まとめ記事は↓
>>「ベクトルとは?ゼロから始める徹底解説記事9選」<<

