
確率連立漸化式(応用編)
今回扱う“確率連立漸化式”は、以前紹介した
・「数列の連立漸化式の解き方」と、
・「確率漸化式(基礎)」の融合分野です。
前回の確率漸化式で登場してきた漸化式は解くことが容易なものでしたが、
今回はそれが連立漸化式に変わるので、少しレベルアップします。
しかし、実際には難関大を中心に(連立)確率漸化式は頻出なので、解法の流れは必ず習得しましょう。
目次(タップした所へ飛びます)
確率連立漸化式の問題
実際に、過去問を通してこのパターンの解法と流れを確認していきます。
少し時間をとって考えて貰ってもいいですし、そのまま解説へ進んでも構いません。
<問題>
AとBの二人が一個のサイコロを以下の手順で投げ合う。
1回目はAが投げる
1、2、3の目が出たら次も同じ人が投げる
4、5の目が出たら、次は別の人が投げる
6の目が出たら、投げた人を勝者としてそれ以降はサイコロを投げない
問一:n回目にAがサイコロを投げる確率Anを求めよ。
問二:ちょうどn回目のサイコロを投げた時にAが勝つ確率Pnを求めよ。
問三:サイコロを投げる回数がn回以内でAが勝利する確率qnを求めよ。
(2011、一橋大)
<コメント>
このサイトにもよく登場する一橋の良問です。文系数学最高峰とされるだけあって、非常に良質な問題が多いので、理系志望の方も時間があれば数学だけ(特に確率/整数分野)でも過去問を解いておくことをおすすめします。
確率連立漸化式の解答解説
問一:指針として、問題文から確率漸化式を立てるサイン「n回目に〜が・・・」を見つけることができます。
従って、推移図を描いて漸化式を立てていきます。以前の「確率漸化式を立てる問題」は、
Pnと(1-Pn)からPn+1の推移図一枚で良かったのですが、
今回はA、Bの2人がサイコロを振るので、<図1ー上>と<図1ー下>の2種類の推移図を描いて2つの漸化式を立てます。
2種類の推移図を描き連立漸化式を立てる
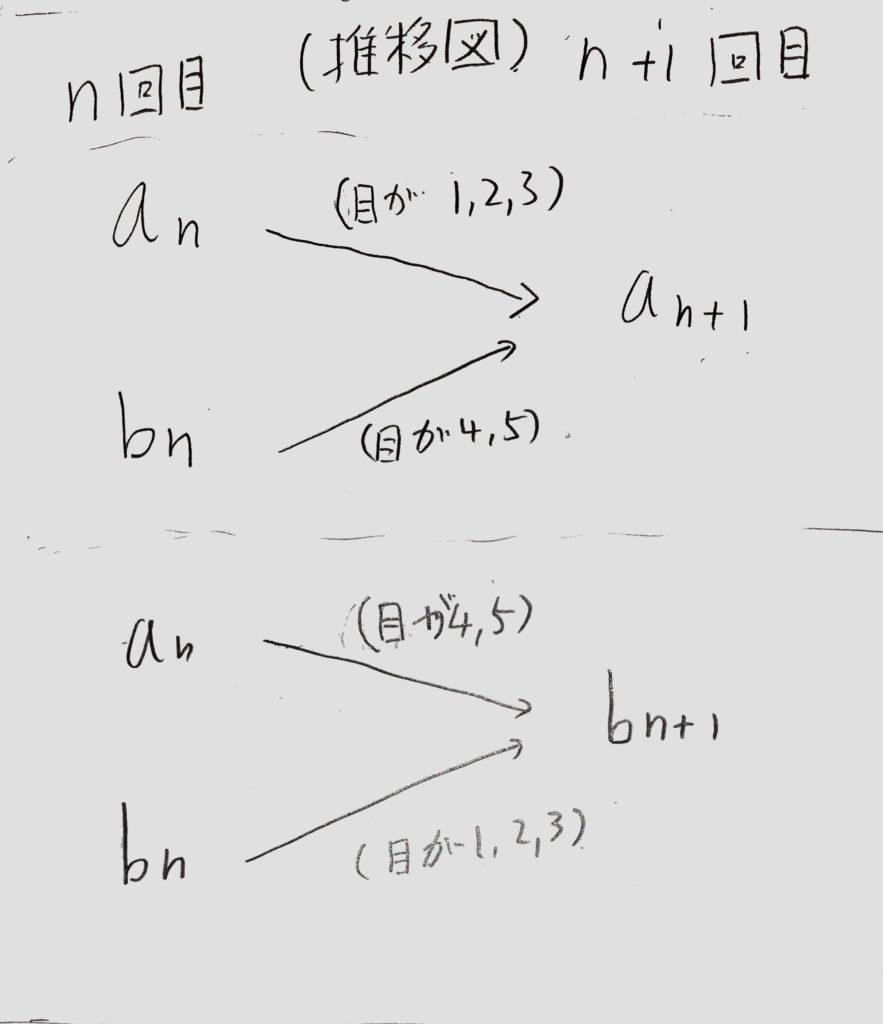
<図1:推移図ー上>と<図1:推移図ー下>
<図1:推移図-上>より一つ目の漸化式は、$$a_{n+1}=\frac {1}{2}a_{n}+\frac {1}{3}b_{n}$$
<図1:推移図-下>より、もう一つは、$$b_{n+1}=\frac {1}{3}a_{n}+\frac {1}{2}b_{n}$$
これは典型的な「係数が対称型の連立漸化式」です!
このタイプは、「和と差を作る」のが定石だったので、(連立漸化式が曖昧な人は→「連立漸化式の解き方」をご覧下さい)
$$和a_{n+1}+b_{n+1}=\frac {5}{6}a_{n}+\frac {5}{6}b_{n}$$
$$差a_{n+1}-b_{n+1}=\frac {1}{6}a_{n}-\frac {1}{6}b_{n}$$
ここで初項A1=1、と初項b1=0(条件より)を確認して、漸化式の和と差をそれぞれcn、dnとおくと
$$a_{n+1}+b_{n+1}=c_{n+1}$$
$$a_{n+1}-b_{n+1}=d_{n+1}$$
$$c_{n+1}=\frac {5}{6}c_{n},c_{1}=1$$
$$d_{n+1}=\frac {1}{6}d_{n},d_{1}=1$$
*2018/11/18:cnの初項とdnの初項をそれぞれ1に訂正しました。
$$故に、 \begin{aligned}c_{n}=a_{n}+b_{n}=1× ( \frac {5}{6}) ^{n-1}\\
a_{n}+b_{n}=( \frac {5}{6}) ^{n-1}\end{aligned}・・・(1)$$
$$\begin{aligned}d_{n}=a_{n}-b_{n}=1× ( \frac {1}{6}) ^{n-1}\\
a_{n}-b_{n}=( \frac {1}{6}) ^{n-1}\end{aligned}・・・(2)$$
$$(1),(2)式より、a_{n}=\frac {1}{2}×( (\frac {5}{6}) ^{n-1}+( \frac {1}{6})^{n-1})$$
$$(1),(2)式よりb_{n}=\frac {1}{2}\{ (\frac {5}{6})^{n-1}-(\frac {1}{6})^{n-1}\} $$
これで、anとbnの一般項が求まりました。
問1は、n回目にAがサイコロを振る確率だったので、求めるのはan
$$よって、a_{n}=\frac {1}{2}\{(\frac {5}{6}) ^{n-1}+(\frac {1}{6})^{n-1}\} $$
問二:<方針>n回目にAが勝利するには、まずAがn回目にサイコロを振る必要があり、かつ、6の目を出すことが必要です。
n回目にAがサイコロを振る確率は(1)よりAn
その時サイコロの目が6である確率は1/6だから、
$$p_{n}=\frac {1}{6}a_{n}$$
$$p_{n}=\frac {1}{6}×\frac {1}{2}\{( \frac {5}{6}) ^{n-1}+( \frac {1}{6}) ^{n-1}\} $$
$$よって、p_{n}=\frac {1}{12}\{(\frac {5}{6})^{n-1}+(\frac {1}{6})^{n-1}\} $$
問三:n回以内にサイコロを振ってAが勝利するには、
qnはPnの時(n回目で勝つ)
Pn-1の時(n-1回目で勝つ)
・・・
・・・
・・・
P2の時(2回目で勝つ)
P1の時(1回目で勝つ)
と1回振っただけで勝つ確率から、n回振って勝つ確率までを全て足し合わせる必要があります。
従ってここで総和=Σ計算をして行きます。
Σの再確認をしたい人は→数列の和とシグマ計算
$$\sum ^{n}_{k=1}p_{k}=\sum ^{n}_{k=1}\frac {1}{12}\{(\frac {5}{6})^{k-1}+( \frac {1}{6}) ^{k-1}\} $$
$$=\frac {1}{12}\sum ^{n}_{k=1}( \frac {5}{6}) ^{k-1}+\frac {1}{12}\sum ^{n}_{k=1}( \frac {1}{6}) ^{k-1}$$
$$=\frac {1}{12}× \frac {\{ 1-( \frac {5}{6}) ^{n}\} }{1-\frac {5}{6}}+\frac {1}{12}× \frac {\{ 1-( \frac {1}{6}) ^{n}\} }{1-\frac {1}{6}}$$
$$=\frac {6}{12}× \{ 1-(\frac {5}{6}) ^{n}\} +\frac {1}{10}×\{ 1-(\frac {1}{6})^{n}\} $$
$$\begin{aligned}=\frac {1}{2}-\frac {1}{2}( \frac {5}{6}) ^{n}+\frac {1}{10}-\frac {1}{10}( \frac {1}{6}) ^{n}\\
=\frac {3}{5}-\frac {1}{2}( \frac {5}{6}) ^{n}-\frac {1}{10}( \frac {1}{6}) ^{n}\end{aligned}$$
まとめ
いかがでしたか?ご覧の通り、連立漸化式は自由に使いこなせることは前提条件であり、その漸化式を立てるまでが勝負になって来ます。
類題は豊富にあるはずなので、是非取り組んでみて下さい!
質問・記事について・誤植・その他のお問い合わせはコメント欄までお願い致します!
お役に立ちましたら、シェア&当サイト公式Twitter(@linkyjuku_tweet)のフォローをお願いします!
今回もご覧いただき有難うございました。

