
イオン化傾向シリーズ第二回
前回、「イオン化傾向とは?その覚え方と電池への応用」ではイオン化傾向の覚え方と、
そのイオン化したい「キモチ」の差を利用して電流を流す「ボルタ電池」と「ダニエル電池」の仕組みを解説しました。
今回は、電池や電気分解の計算に必須の電気量とファラデー定数に付いて学んだあと、ダニエル電池の実践的な問題を解いていきます。
いずれも頻出問題なので必ず解けるようになりましょう。
※「リチウムイオン電池(二次電池)の仕組みと歴史」を作成しました。
目次(タップした所へ飛びます)
ダニエル電池の計算問題とファラデー定数
実際に問題に入る前に、おさえておく必要のある「ファラデー定数」「電気量」について紹介しておきます。
電池/電気分解に必須の電気量とファラデー定数
電池や電気分解の問題では、流れた電気量が電子何mol分か?
に換算して様々な問題を解いていくことになります。
ここで、1A(アンペア)の電流が1s(秒間)流れた時の電気量を1(C)と定義します。
また、電流が流れるということは、電子が逆方向に移動しています。
しかし電子1個1個の持つ電荷(素電荷、電気素量と言います)は非常に小さいです。
そこで、この電子1個分の電気素量をアボガドロ定数個掛けたもの、つまりおよそ\(6.02\times 10^{23}個=1molの電子が持つ電気量\)のことをF(C/mol)という記号で表します。
そして、F≒96500(C/mol)という関係があります。このFをファラデー定数と言います。
色々と単位や数字が出てきますが、「1(A)× 1(s)=1(C)」及び、「電子1個分の電気量(C) × アボガドロ定数(6.02×1023(個/mol)=F=96500(C/mol)」はおさえておきましょう。
電流とファラデー定数の練習問題
軽めの計算問題で、ファラデー定数を使えるように訓練しておきます。
以下の例題では、ファラデー定数F=96500(C/mol)、アボガドロ定数を6.02× 1023 (個/mol)とする。
例題1:10Aの電流を10分間流した時、電子は何mol移動したか
例題2:1.5Aの電流を16分5秒間流した時、電子は何個分移動したか。
それぞれ有効数字2桁で答えよ。
解答1:10Aが10分とあるので、まず電気量C(クーロン)の計算をします。
そのとき、時間の単位は秒であることに注意しましょう。
10[A]× ( 10×60)[s]=6000[C]
上のように、600秒に直してから計算すると6000(C)流れたことが分かりました。
この例題では「電子何mol分流れたか」を問われているので、この電気量をファラデー定数Fでわります。
$$\frac {6000[C] }{96500[ C/mol] }=0.0631,,,(mol)$$
従って、有効数字2桁で答えると、6.3× 10-2(mol)
解答2:同様に時間を秒単位に変換していきます。
16×60 =960(s)、1.5(A)× (960+5)(s) ここで、ファラデー定数でわると物質量が出てきます。
$$\frac{1.5×965}{96500} $$
さらに「個数」を聞かれているので、アボガドロ定数を掛けます。
$$従って、\frac {1.5×965}{96500}×6.02×10^{23}=9.03×10^{21}$$
有効数字2桁より、9.0× 1021 個
・・・(答)
ダニエル電池の計算問題(極板の質量変化)
では、いよいよダニエル電池の問題に入っていきます。
今回は
(1)電流と時間から電気量を求め、
(2)ファラデー定数で割って電子のmol数を計算して、
(3)最終的に極板の質量の変化量を求める
という流れになっています。
この解き方の流れは他の電池や電気分解でも良くあるパターンなのでぜひ身につけて下さい。
(問)
以下の<図1>のような仕組みをした電池がある。
2つの極板の間は素焼き板で仕切られており、
亜鉛極板側の電解液\(ZnSO_{4}aq\)と銅極板側の電解液\(CuSO_{4}aq\)は互いに混ざらないが、\({SO_{4}}^{2-}やZn^{+}\)などのイオンは素焼き板を移動することが出来る。
必要ならば、以下の数値を使って有効数字二桁で解答せよ。原子量Cu:64、S:32、O:16、Zn:65
ファラデー定数:F=96500(C/mol)
問1:0.5Aの電流を 2時間40分50秒間流した時、移動したe-の物質量を求めよ。
問2:正極での化学反応式を書き、問1の終了時に正極で増えた質量を求めよ
問3:負極での公式反応式を書き、同様に負極で減った質量を求めよ
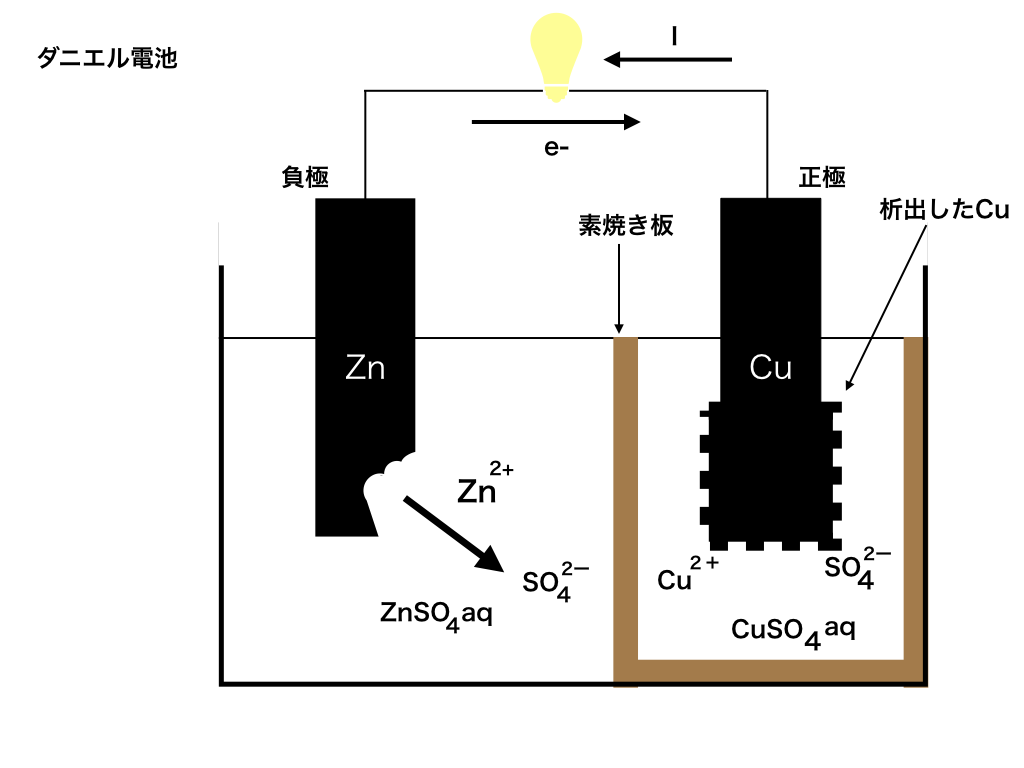
<ダニエル電池>
解答編
解答1:移動した電子のmol数を計算する
まず、2時間40分50秒を秒に変換します。
3600× 2+40× 60+50=9650
(A:アンペア)× (s:時間)=C:電気量
$$0.5\left( A\right) \times 9650\left( s\right) =4825\left( C\right)$$
ファラデー定数で割って、
$$\frac {4825\left( C\right) }{96500\left( C/mol)\right) }=\frac {1}{20}\left[ mol\right]$$
従って、5.0× 10-2 mol
解答2:銅板の質量増加分を計算する
\(Cu^{2+}+ 2e^{-}→ Cu\)
ここで、解答1より問題の時間中に0.05(mol)の電子が流れたので、
上記の式の\(2e^{-}が0.05(mol)\)に当たります。
次に、反応式の係数を見ると、電子:Cu=2:1なので、電子の半分の物質量の銅が析出したことになります。
つまり2時間40分50秒で析出した銅は、0.025(mol)。
問題では「質量」を問われているので、64× 0.025= 1.6(g)増加する。
解答3:亜鉛板の質量減少分を計算する
\(Zn → Zn^{2+} +2e^{-}\)
より、(問2)同様、0.025(mol) 分の亜鉛がイオン化(溶け出して)いるのでその分質量が減少します。
よって、亜鉛Znの原子量は問題文より65。
従って、65× 0.025(mol)=1.625(g)
有効数字二桁より、1.6(g)減少する。
・・・(答)
まとめと次回予告(電気分解)
・電気化学(電池や電気分解など)では、ファラデー定数や、電気量などをしっかり理解する必要があるので繰り返し復習してください
・次回(酸化還元反応第4回)は、電池と逆に外側から電気を与える「電気分解」に付いて紹介していきます。
電気分解は、メッキや純銅の精錬などに応用され日常生活に無くてはならないものです。
また、この分野は無機化学と重なるところがあり良く理論化学との融合問題が出題されます。
酸化還元反応シリーズ
第1回:「酸塩基反応と酸化還元反応の違いを答えられますか?」
第2回:「イオン化傾向と酸化還元反応(電池)」
第3回:「ダニエル電池の計算問題とファラデー定数」<今ココです>
第4回:「電気分解とは?電池との違いと陽極/陰極でのルール」
第5回:「イオン化傾向とイオン化エネルギーの違いとは?」
<最新記事>「リチウムイオン電池の仕組みと歴史」を読む。
今回も最後までご覧いただき有難うございました。
お役に立ちましたら、シェア&当サイト公式Twitter(@linkyjuku_tweet)のフォローをお願いします!
質問・記事について・誤植・その他のお問い合わせはコメント欄(もしくはtwitter )までお願い致します。

