コンデンサーの電気容量を変えるパターン
<この記事の内容>:前回の記事→「コンデンサーの仕組みと公式が分かる!」に引き続き、コンデンサーについて扱います。
コンデンサーの電気容量の公式を元に、誘電体や誘電率・比誘電率、
誘電分極の意味とそれらが与える影響、更にコンデンサーの並列接続と直列接続の解説を行います。
目次(タップした所へ飛びます)
電気容量の意味と変化
・電気容量のおさらい
・誘電率と真空の誘電率・比誘電率
・誘電体(不導体)の誘電分極と導体の静電分極
・誘電体を入れると電気容量が増す!
・コンデンサーの並列接続と直列接続
・まとめ(NEW!:電磁気まとめページへ)
電気容量のおさらい
電気容量はコンデンサーが蓄えられる電荷を示すもので、その単位は、F:ファラドでした。
現実には電気容量が、1(F)というコンデンサーは一般的でない(大き過ぎる為)、
$$μF(マイクロファラド:1\times 10^{-6})$$
$$やnF(ナノファラド;1\times 10^{-9})$$
等の単位をつけられている場合が多いです。
極板間が真空のコンデンサーの電気容量の公式は、Cを電気容量として、ε0:真空の誘電率、d:極板間距離、S:極板の面積を用いて現されました。
$$C=\varepsilon _{0}\frac {S}{d}$$
誘電率と真空の誘電率、比誘電率の違い
ところで、ε(イプシロン)で表される誘電率とは一体なんなのでしょうか?
単位を見てみると、誘電率:ε(F/m)となっています。これは「外部から電場をかけた時の誘電体の分極具合」を表すもので、誘電体の種類によって値が変わります。
誘電体の分極は下の「誘電分極とは?」をご覧下さい。
最初に習うのが真空中の誘電率ε0です。次に誘電率ε、これは上記の様に物質によって数値が異なります。
最後に比誘電率εr、これは単位がない数で、誘電率と真空の誘電率の比を表し、ε=ε0・εr
$$\varepsilon =\varepsilon _{0}\cdot \varepsilon _{r}$$
のように、真空中に比べて、何倍その誘電体が分極しやすいかを示す数となります。
誘電体の誘電分極と導体の静電分極
一応確認しておきます;誘電体と導体の違い
誘電体は電気を通しにくい
誘電体は電気を通しにくい物質で出来ていて、電子が上手く自由に移動できないので、僅かに分極を起こします。
導体は電気を通すもの
導体は電気を通しやすく(=電子が自由に動ける)ので、容易に分極を起こし、これを静電分極といいます。
誘電分極とは?
誘電体を電場Eがかかっている空間に入れると、誘電体内部にある原子一つひとつが持っている、
電子(eー)と原子核(陽子p +と中性子)が、僅かに電場によるクーロン力Fによってズレます。この現象を誘電分極と言います。
具体的に充電されたコンデンサーの中に入れた場合を考えてみます。
上極板が正電荷を帯びているときは、誘電体中の原子の電子(e-)がクーロン力によって上に引っ張られ、
下極板はその時負電荷を帯びているので、原子核(正確には陽子)が同様に下に引っ張られることで誘電体内部で電荷の偏りが起きます。
しかしあくまで「誘電体=不導体」なので、導体の「静電分極」に比べると分極による影響は小さいです。
誘電体(比誘電率εr)を入れる事によって電気容量が増加する2パターン
(1)電源をつないだ状態で誘電体を入れる場合
この場合は、Q=CVの式の内、電圧は一定です。
そして、電気容量Cは誘電体によってεrCに増加するので、結果として電気量Qもεr倍されます。
(2)電源を切った・スイッチを外した状態で誘電体を入れる場合
この時は、電源と繋がっていない=電荷が流れ込まない=Q一定、
そしてQ=CVの式を見るとCはεr倍されているので、電圧Vが調整の為、1/εr倍に下がります。
⑴、⑵の電気容量はどんな状況であっても同様にεr倍されている=電気容量は増えています。
コンデンサーの直列接続と並列接続
コンデンサーの接続と抵抗の接続は計算の仕方が直列と並列で逆になっているので注意が必要です。
ここでもう一度電気容量の式を見てみると、
$$C=\varepsilon \frac {S}{d}$$
「距離に反比例し、面積に比例する」事がわかります。
詳しくは(復習)「コンデンサーの仕組みと公式の意味が分かる!」をご覧ください。
従って、コンデンサーを直列に接続するということは、距離を大きく(極板間距離を広くする)ことに他ならず、単純な足し算では求められません。
$$\frac {1}{C'}=\frac {1}{C_{1}}+\frac {1}{C_{2}}$$
よって、直列の合成電気容量は各コンデンサーの電気容量の逆比の和で表されます。
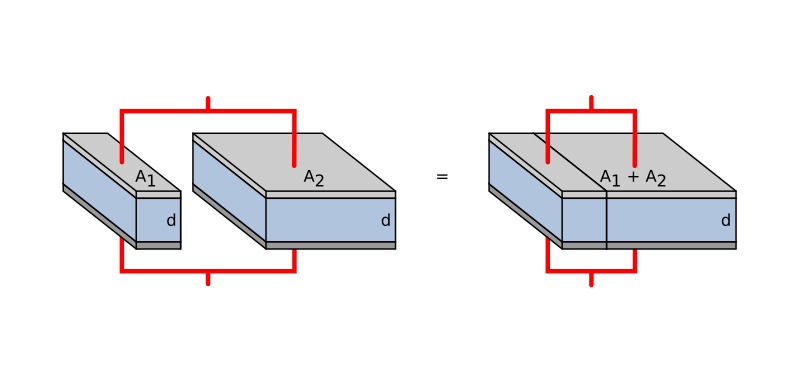
一方で、コンデンサーの並列接続は面積を広くするという風にみることができ、電気容量の単純な足し算が成立します。
$$C'=C_{1}+C_{2}$$

電気容量を変化させる方法まとめと電気回路へ
電気容量Cを変化させる方法は、
・極板間距離を変える
・極板の面積を変える
・誘電体を挿入する
・コンデンサーを直列・並列に接続する
方法があり、試験などではそれぞれを組み合わせて計算させる問題がよく出題されます。
電気回路の解き方シリーズへ
また、電気回路以降に進むと、これらの計算は自由自在にできることを前提として様々な応用をする事になるので、今の内に意味をしっかり理解しておく様にしましょう。
<第一回>「電流とは?I=envSの式の導出からオームの法則まで徹底解説」
<第二回>「非オーム抵抗の問題の解き方と交点が解となる仕組み」
<第三回>「キルヒホッフの法則を理解して、電気回路の問題を解く」
<電気・磁気分野のまとめページ>:「高校物理・物理基礎の電磁気分野の記事まとめ」左のページから、電気・磁気についての各記事をご覧いただけます。
今回も最後まで読んでいただき有難うございました。
質問・記事について・誤植・その他のお問い合わせはコメント欄までお願い致します!

