
弦の振動/線密度/縦波と横波
<この記事の内容>:片側が音叉(おんさ)やスピーカー、もう一方が重りなどで固定され、両端が固定端となる「弦」の振動について、基礎から有名公式、力学とのちょっとした融合問題まで、イラストを使いながら紹介しました。
<この記事に関係するページ>:「開管・閉管による気柱の共鳴と振動」でも、今回と同様に縦波の振動について解説しています。あわせてご覧ください。
目次(タップした所へ飛びます)
弦の振動(準備編)
弦の振動の前に、『線密度ρ』や力学の振り返りを行います。
線密度と張力・弦を伝わる速さ
$$線密度\rho=\frac{弦の重さ(Kg)}{弦の長さ(m)}$$
$$v=\sqrt{\frac{T(N)}{\rho (Kg/m)}}$$
弦を伝わる速さをVとすると、上のように弦の張力Tを線密度ρ(=弦の重さ/長さ)でわり、ルートをとることで求まります。
(単位を調べてみると、$$分母のT(N)=T(Kg\times \frac{m}{s^{2}})、分子\rhoは\frac{Kg}{m}$$
整理して2乗を外すと確かに\(\frac{m}{s}\)となります。
音叉(おんさ)と弦の振動の問題編
ここから具体的な問題を通して、知識と解法を定着させていきます。
音叉の向きで答えが異なる【要注意】
前半の問題1と後半の問題2の違い(特に問題2)に注意しながら、基本問題の解き方を習得していきましょう。
弦の振動方向と音叉の振動方向が同じ場合
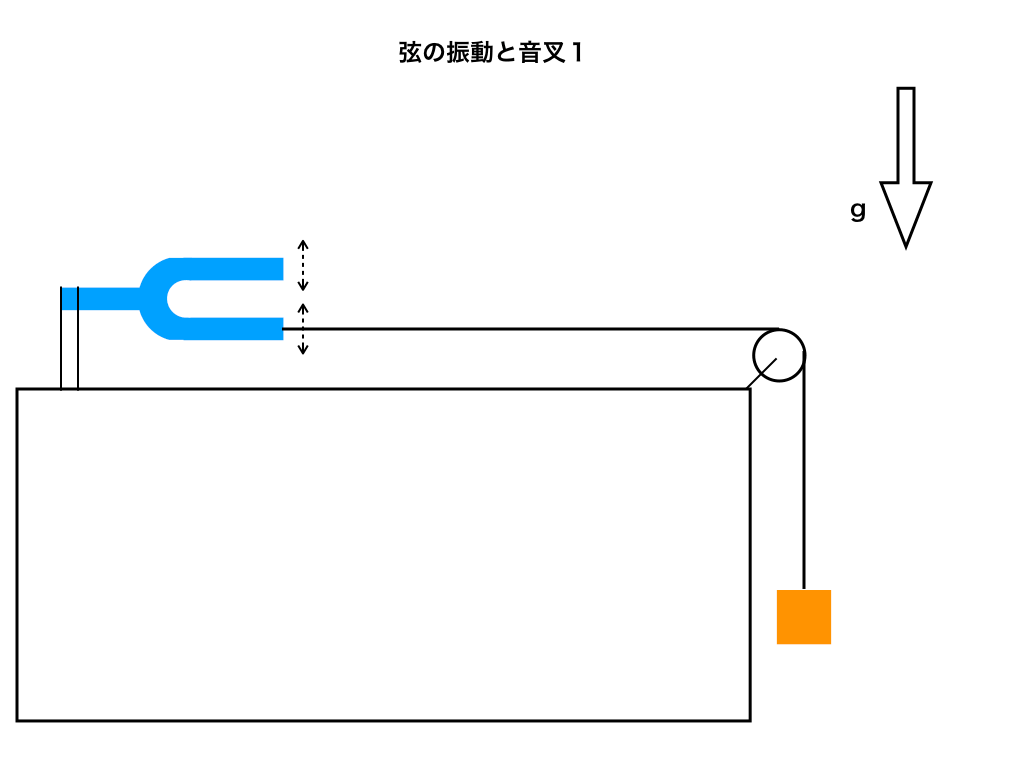
問題1:今以下の<図1>のように、弦の片側を『f(Hz)』で振動する音叉に、もう片方を1(Kg)の重りにつなげた。
音叉から滑車部分までの弦の長さは6(m)で、その質量は0.003(Kg)であった。
重力加速度\(gを9.8(m/s^{2})\)とするとき、次の (1)〜(4)に答えよ。
(1):線密度ρ(Kg/m)を求めよ。
(2):張力Tは何Nか?
(3):弦を伝わる波の速さV(m/s)を求めよ。
(4):おんさから滑車部分までの間に、腹が3つできた。このおんさの振動数f(Hz)を求めよ。
<問題図1>
解説編
問題文は長いですが、ひとつひとつ解いていきましょう。
(1):まずは、「線密度ρ=弦の質量÷長さ」より、\(\frac{0.003}{6}=5.0\times 10^{-4}\)
よって、\(\rho=5.0\times 10^{-4}(Kg/m)\)・・・(1)の答
(2):次は張力です。力の矢印は書き込みませんが、mg=T で釣り合っており、m=1(Kg),g=9.8(m/s^2)であることから、\(T(N)=1(kg)\times 9.8(m/s^{2})\)
より、T=9.8(N)。・・・(2)の答
(3):『弦を伝わる波の速さの公式』より、1と2で求めたρとTを公式に代入して、
$$V=\sqrt{\frac{T}{\rho}}=\sqrt{\frac{9.8}{5.0\times 10^{-4}}}$$
これを解くと、\(V=10\sqrt{196}=140(m/s)\)・・・(答)
(4):いよいよ最後の問題です。
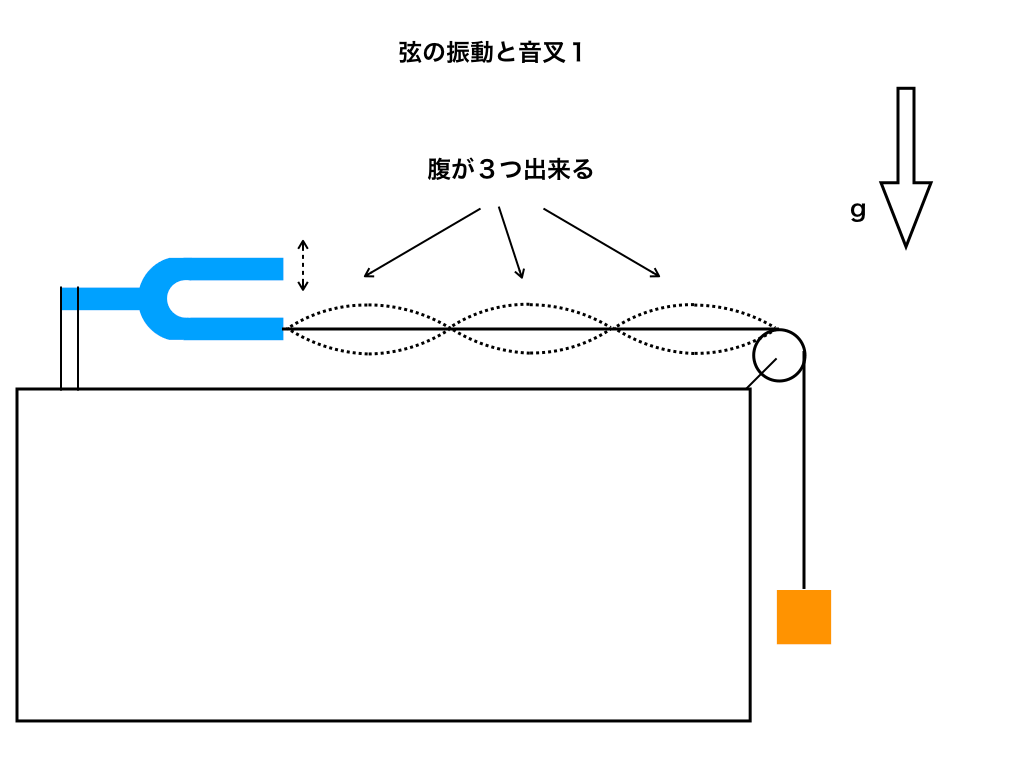
弦に腹が三つできた(下の図2参照)ということは、6mの弦が定常波の波長3/2つ分\(=\frac{3\lambda}{2}\)であることが分かります。
よって、\(\lambda=4(m)、V=\lambda\times f \)の公式に当てはめると\(140=4\times f \)。
ゆえに、振動数:f=35(Hz)・・・(答)
<解答イラスト2(問4)>
90度違う場合
上述したように、この弦の振動方向(上下方向)と、おんさの振動方向(左右)が違う場合は特によく出題され、間違えやすいので注意が必要です。
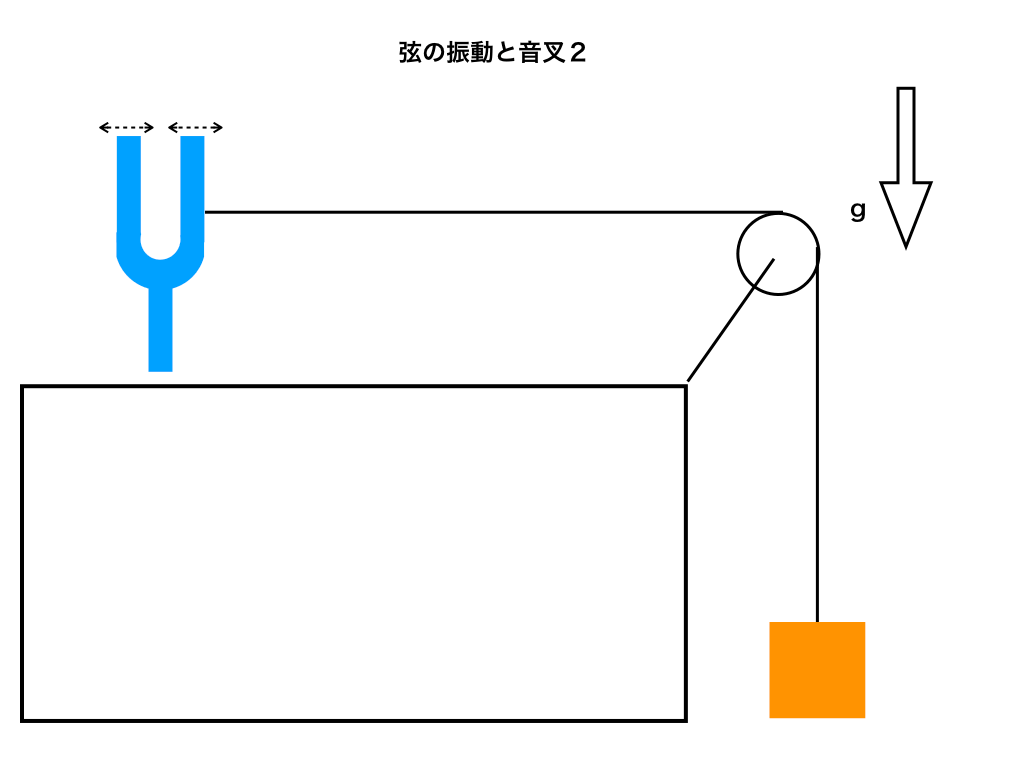
問題2:弦の長さや質量、張力などの各条件は問題1と同じで音叉のみ弦と垂直に向きを90°変えた。このとき、弦の振動数は何Hzになるか答えよ。
解説編
解答(問題2):これは一度やっておかないと戸惑う問題です。
横向きの音叉の場合は、弦と音叉の振動数が一致していました。
が、向きが90°変わって、垂直になると音叉の半分の振動数が弦の振動数と同じになります。
(音叉が図2の横向きに一周期振動する間、弦は半周期分しか振動していません)
したがって、f/2=17.5(Hz)・・・(答)
定着問題
音叉の代わりに、振動数が400(Hz)のスピーカーを問1の様に取り付けると、20個の腹が出来た。
弦の長さが0.1(m)、\(線密度\rho=5\cdot 10^{-3}(N/m)\)である時
(一):波長λ
(二):弦を伝わる速さV
(三):弦にかかる張力の大きさ
をそれぞれ求めよ。
解答解説(定着問題)
解答(一),(二):弦からスピーカーに変わっていますが、問題1と同じように解いていけば良いです。
重りの質量がわかりませんが、20個の腹が0.1(m)の弦に出来ていることから、10波長(λ)分の長さが0.1(m)にあたります。λ=0.01(m)
よって、V=fλより\(V=400\times 0.01 \leftrightarrow V=4(m/s)\)
解答(三):$$V=\sqrt{\frac{T(N)}{\rho (Kg/m)}}$$
この公式を思い出して、$$4=\sqrt{\frac{T}{5\cdot 10^{-3}}}$$
これを計算すると、張力は正なので、\(T=8.0\times 10^{-2}(N)\cdots (答)\)
弦の振動まとめ
・波動の分野の中でも、力学の知識が若干必要とされます。
・弦と波の進む方向について(今回の問1・問2)は非常によく問われるので、振動方向同じ→f同じ。
振動方向が垂直→fが半分。という事を必ず頭に入れておきましょう。
物理:波動の関連記事へ
最後までご覧いただきまして、ありがとうございました。
当サイト:「スマホで学ぶサイト、スマナビング!」では、読者の皆さんのご意見・ご感想の募集をコメント欄で行なっています。
・お役に立ちましたら、snsなどでシェアをしていただけると、とても励みになります。
・お問い合わせ/ご依頼/その他のご連絡は、別途【運営元ページ】よりお願いいたします。

