
比例式/相反方程式(数Ⅱ:式と計算)
この記事では、数学2で扱う『比例式』、『相反方程式』のような解法(式変形)を知っておきたい(知らないと初見では解けないことが多い)少し特殊な式について、問題を解きながら整理しています。
関連まとめ:「方程式・不等式の分野横断型まとめページ」
目次(タップした所へ飛びます)
比例式とは
比例式とは、次の項で紹介するような(分数)=(分数)=(分数)のような形や、名前の通りA:B=C:Dのような比例の形で表されている式のことです。
この比例式の関しては、
・”求値”問題
・”証明”問題
の2つのアプローチで出題されるので、それぞれの代表的な問題を紹介します。
比例式による求値問題
求値問題(1):
$$\frac{p+q}{3}=\frac{q+r}{4}=\frac{r+p}{5}$$
の時、$$\frac{pq}{pq+qr+rp}$$の値を求めよ。
=k(定数)とおく:重要な解法
このような比例式は、「(式)=(式)=(式)=k」のように、(kでなくとも、文字はなんでも構いません。)
とにかく定数を文字でおき、(式)=・・・(式)=文字定数 のカタチに持っていきます。
$$\frac{p+q}{3}=\frac{q+r}{4}=\frac{r+p}{5}=k$$として、
p+q=3k・・・(*)
q+r=4k・・・(**)
r+p=5k ・・・(***)
更に、(*)~(***)までを全てたすと、
2p+2q+2r=12k,すなわち、p+q+r=6k となります。
ここで、p+q+r=6k から(*)式を引くと、p+q+r-(p+q)=6k-3k となって、
r=3k と求めることができます。
p,qについても同様の手順を踏むと
(p,q,r)=(2k,k,3k)・・・(****)
ここで、$$\frac{pq}{pq+qr+rp}$$の値を求めるために、上のp,q,rをそれぞれ代入すると、
$$\frac{2k^{2}}{2k^{2}+3k^{2}+6k^{2}}=\frac{2k^{2}}{11k^{2}}$$
・・・これは分母・分子に”kの2乗”があるので打ち消すことができますね!
よって、(1)の答えは\(\frac{2}{11}\)・・・(終)
比例式の証明問題
求値問題の次は、証明問題に移ってみましょう。
こちらも”係数が違うだけ”のなどの類題が多数有る問題で、テストで出てくれば必ず得点しておきたいところです。
問題:\(p:q=r:s\)のとき、$$\frac{p-5q}{2p+q}=\frac{r-5s}{2r+s}$$を示せ。
解説・証明
指針は証明問題に変化しても同じです。
ここでは、(分数)=(分数)の形になっていませんが、内項の積・外項の積から変形すると、求値問題と同じ様に解いていくことが可能です。
p:q=r:s
$$sp=qr ∴ \frac{r}{s}=\frac{p}{q} $$これを=kと置いて
p=qk
r=sk
証明する式の右辺と左辺に分けて、それぞれ代入します。
$$(左辺)=\frac{p-5q}{2p+q}=\frac{qk-5q}{2qk+q}=\frac{q(k-5)}{q(2k+1)}=\frac{k-5}{2k+1}$$
同様に、r=skから
$$(右辺)=\frac{r-5s}{2r+s}=\frac{sk-5s}{2sk+s}=\frac{k-5}{2k+1}$$
以上より、左辺と右辺が等しいので、題意は示された。
相反方程式とは
”相反方程式”という名前を初めて聞いた人もいるかもしれません。
相反する(あいはんする)方程式とは、以下の項の具体例で扱いますが、xの高次方程式の中でも次数が丁度真ん中を境に係数が対称になっているものをいいます。↓↓
相反方程式の具体例(と問題)
実例を見た方が早いので、相反方程式の例題を解いていきましょう。
例題:以下の方程式(1)および(2)を解き、xの値を求めよ。
四次の相反方程式
\(x^{4}+4x^{3}+6x^{2}+4x+1=0\cdots (1)\)
このように、この四次方程式では4次〜0次(定数項)までの中心にある”xの二乗”の左右でxの○乗の係数が綺麗に対称になっています。
さらに”高次”の方程式
もう一つ、5次の相反方程式も見ておきます。
\(x^{5}+5x^{4}+10x^{3}+10x^{2}+5x+1=0\cdots (2)\)
では、例題のようにこれらの方程式を解いていきましょう。
解法の解説1:(4次の場合)
初めに述べたとおり、このような方程式が登場した際の解法は決まっており、知っていないとその場で思いつくのは難しいのでしっかり覚えておきましょう。
x≠0を示す
相反方程式を見たら、中央の次数(ここでは\(6x^{2}\))が定数項となるように式変形するのが鉄則です。
そのためにも、ここでは\(x^{2}\)で両辺を割らないといけない(下)のですが、もしx=0ならばそれができません。
記述式などで減点されないように、しっかりと\(x≠0→x^{2}≠0\)であることを示しておきましょう。
x=0とすると、(1)のxにゼロを代入したとき【1=0】となる。ゆえにx≠0。
この証明法は「背理法の意味と証明問題での使い方」でより詳しく解説しています。
\(x^{2}≠0\)より、両辺を割る
さてx≠0 なので、\(x^{2}≠0\)。
これで安心して両辺をxの二乗でわることができます。
$$x^{2}+4x+6+\frac{4}{x}+\frac{1}{x^{2}}=0$$
x+1/xを文字でおき新たな文字の2次方程式へ帰着させる
ここで、最大のポイント:$$『x +\frac{1}{x}』を文字でおく$$という方法を用います。
\(x+\frac{1}{x}=l \)とすると、\(\left(4x+\frac{4}{x}=4l\right)\)であらわすことができるので、
残りの\(\left(x^{2}+\frac{1}{x^{2}}\right)\)も"l”であらわすことを考えます。
$$l^{2}=x^{2}+2+\frac{1}{x^{2}}$$
だから、$$l ^{2}-2=x^{2}+\frac{1}{x^{2}}$$
よって(1)式は、\(l^{2}-2+4l+6=0・・・⭐︎\)
⭐︎をlについて整理し、因数分解して\((l+2)^{2}=0\)
l=-2
\(x+\frac{1}{x}=-2\)
\(x^{2}+2x+1=0\)
したがって、x=-1 ・・・(答)
解説2:(5次の場合の解を求める)
五次の場合は先ほどの方法がそのまま使えません。
それならば、(1)の形になる様に次数を下げることを考えてみます。
次数を下げる(重要テクニック)
普通ならば、x=±1、±2・・・と代入していく(「因数定理と式の割り算の解説」)のですが、ココで数字を入れてチェックする前に気付いておきたい事があります。
この相反方程式は、係数が同じ”変数xの○乗”の部分が丁度”偶数と奇数のペア”になっている事がわかるでしょうか?(下の図参照)↓
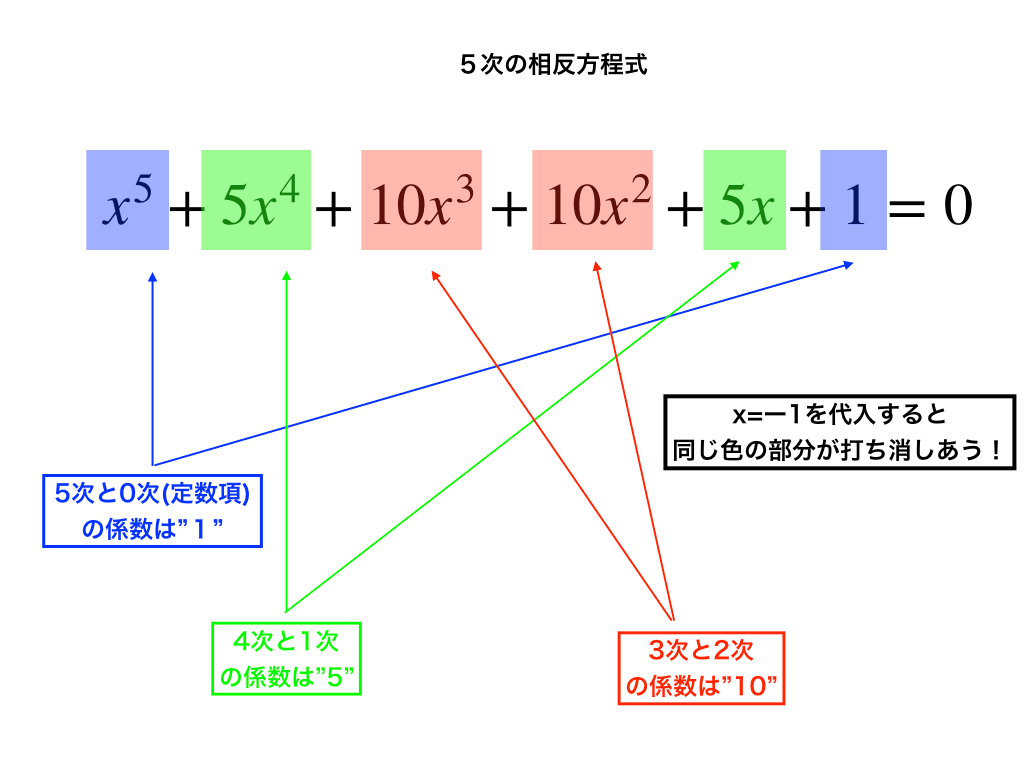
\(x^{5}+5x^{4}+10x^{3}+10x^{2}+5x+1=0\)
したがって、x=ー1を代入するとうまく全てが打ち消しあって=0となるのです!
4次の方程式の部分を同様にして解く
こうして、xの解ひとつ(−1)が求まり、(x+1)で(2)式をわると
次のように4次方程式が求まります。
$$(x+1)(x^{4}+4x^{3}+6x^{2}+4x+1)=0$$
(1)より\((x^{4}+4x^{3}+6x^{2}+4x+1)=0\)の解は"ー1"だったので、結局5次方程式の解は全て”-1”であることがわかります。
よって、x=-1・・・(答)
式と計算まとめへ
さて、今回は式と計算・証明分野で頻出、かつ、知識のあるなしで差がつく2単元を解説しました。よく復習して、時間があれば類題・応用題を探して何度か繰り返しておきましょう。
関連記事へ
【高次方程式と式と証明】←一覧へ

