キルヒホッフの(第一・第二)法則と直流回路
<この記事の内容>:「電流とは?I=envSの式の導出法」
に引き続き、高校物理・物理基礎の電磁気から、
・”電流・直流回路の問題の解き方の基礎”
とそのために必須の
・『キルヒホッフの法則(第1・第2法則)』を図解していきます。
目次(タップした所へ飛びます)
キルヒホッフの法則とは
キルヒホッフの法則と聞くとなんとなく難しそうに思えるかもしれませんが、ごく当たり前のことを言っているだけなので、気軽に読み進めてください。
また、第一と第二の2つの法則があるので、それぞれに分けて紹介していきます。
キルヒホッフの第一法則
キルヒホッフの”第1”法則は、「ある点に”流れこむ電流の総和”と”流れ出る電流の総和”が等しい」という事を言っています。下の図を見ればすぐに当たり前だなと気づくでしょう。
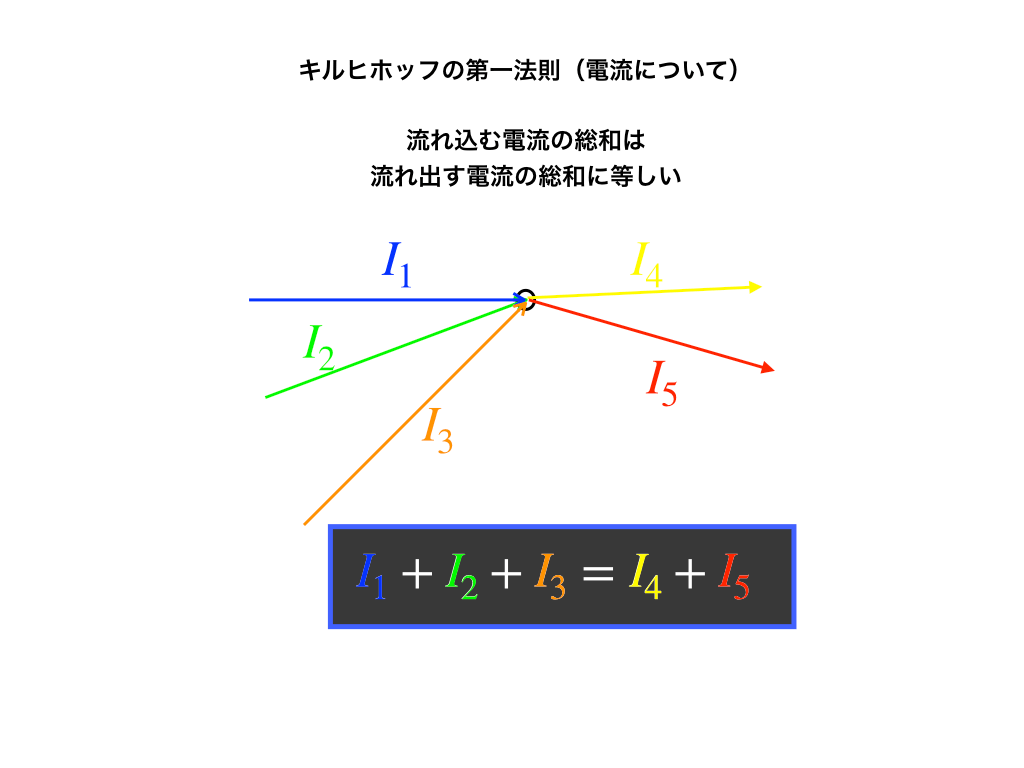
$$I_{1},I_{2},I_{3}$$が一点に流れ込んでいるので、そこから出る電流の総和である$$I_{4}+I_{5}$$が等しいという事です。
キルヒホッフの第二法則
キルヒホッフの”第二”法則は、【電圧】について扱います。
例えば次のような回路で考えてみます。電池によってに持ち上げられたVが一周すると元の位置に戻っています。(<図2>)
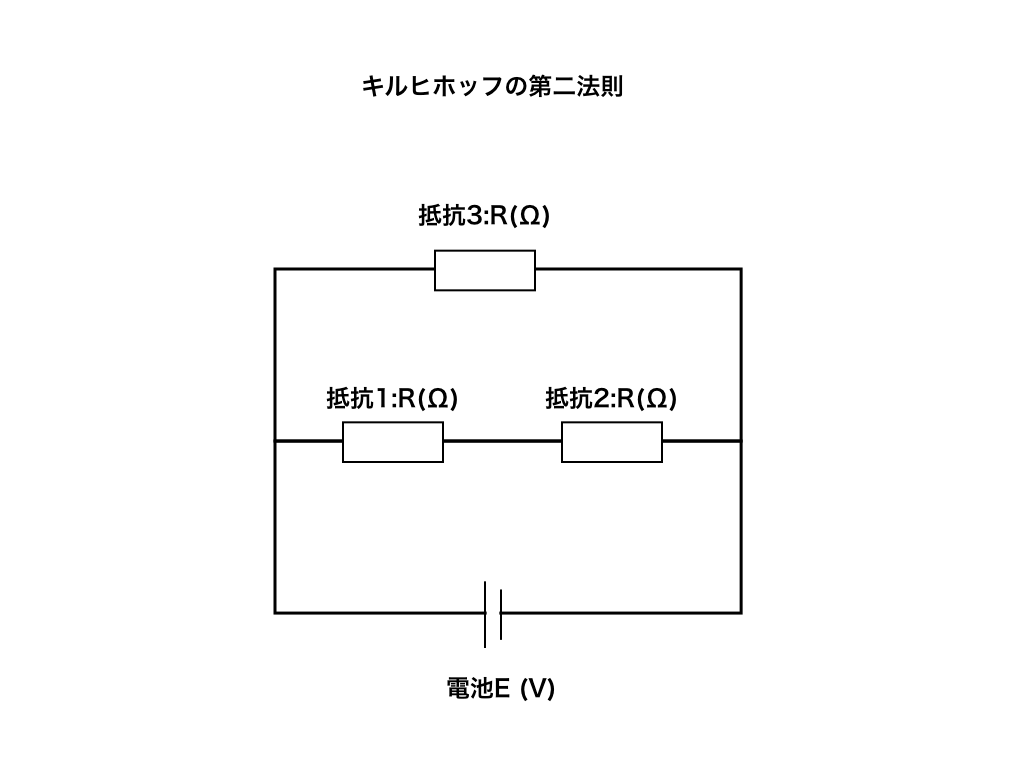
抵抗が3つ(2つが直列・もう1つと並列)で起電力E(V)の電池が接続された回路です。
これを、次の図のように電位を”電気的な高さ”と考えて、
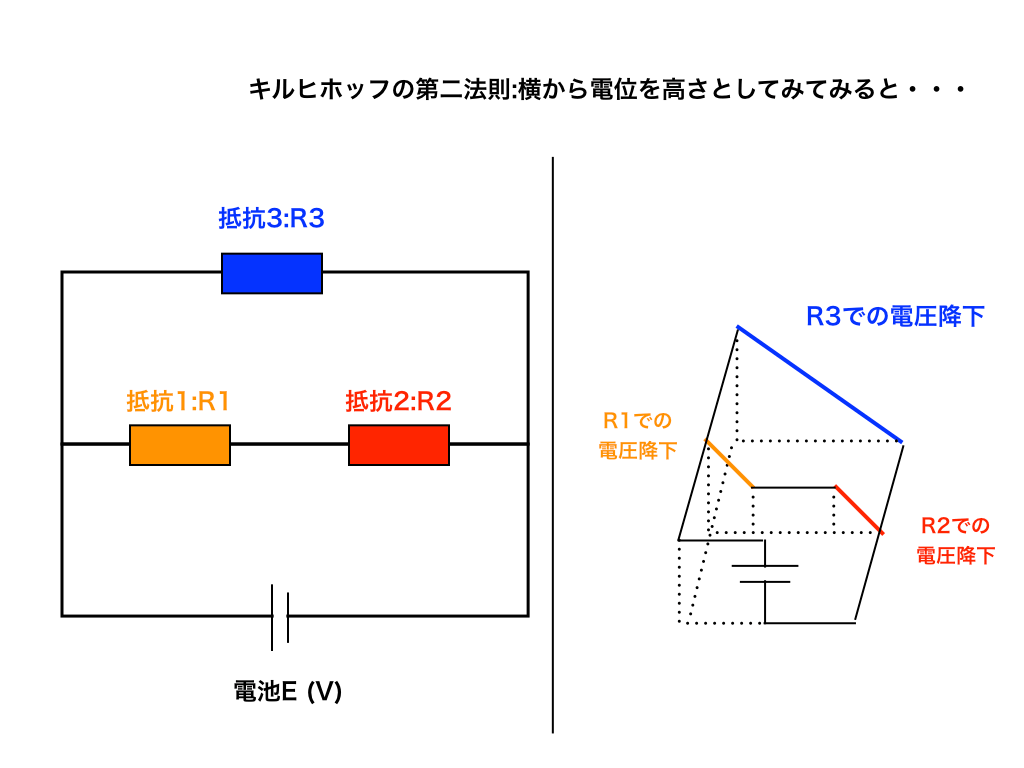
<図2>
すると、右のように電池によって上がった電圧が、直列抵抗の部分では2段階(抵抗R1とR2)に分かれて元の0(V)に戻り、抵抗が1個の青線部分は直接E(V)から0(V)に降っていることがわかります。
これらをまとめると、
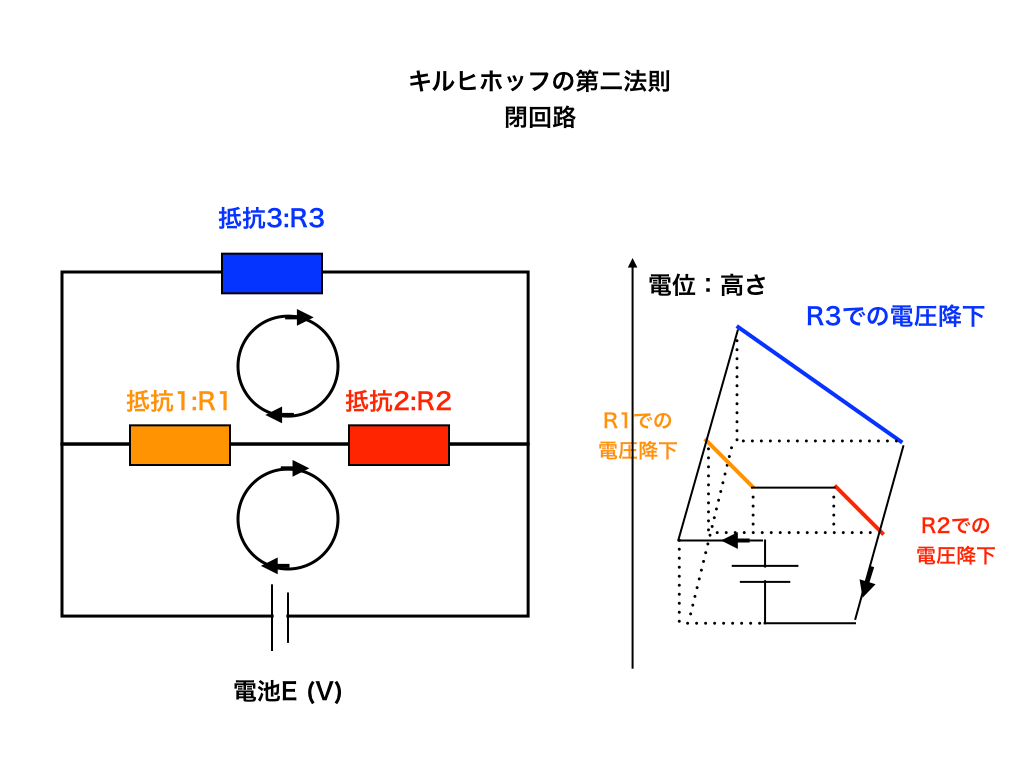
上の図のように、『閉じた回路』では、ぐるっと一周して電位が0になる=起電力と抵抗による電圧降下の総和が0になるということが確認できます。
これが『キルヒホッフの第2法則』の意味です。
直流回路の問題でキルヒホッフの法則を使う
ここまで、キルヒホッフの法則について解説してきましたが、実践的にはこれを使いこなして問題を回答しなければなりません。
特に【第二法則】で扱っている『閉じた回路を1周すると電圧の総和が0になる』ということは、今後電気回路の問題を解いていく上で不可欠なものなので、ぜひこの例題を通して使い方の《基礎》を習得しましょう!
練習(定着用)問題
初めはごく簡単なレベルから解いて行きます。
例題1:いま以下の図のように起電力5(V)の電池と、抵抗値2(Ω)の抵抗を結んだ回路がある。この時の抵抗1での電圧降下の値(V)と電流の大きさ(A)を求めよ。
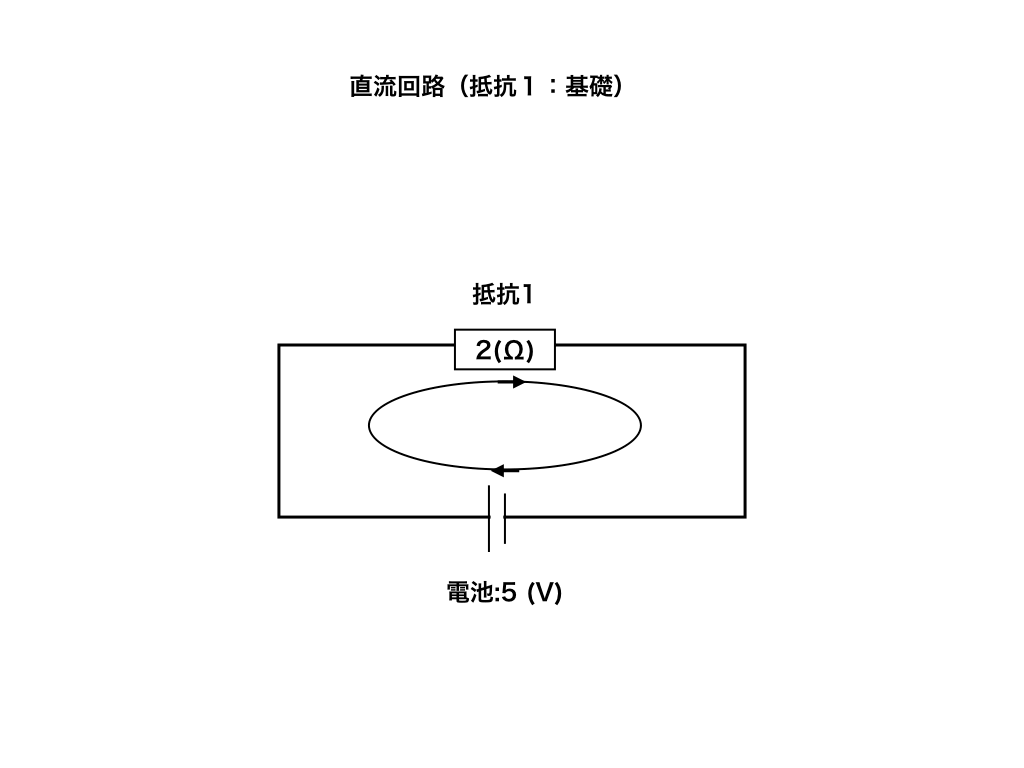
例題2:同様に、起電力5(V)の電池と2(Ω)の抵抗3つを次のように接続した時、R1,R2,R3のそれぞれの電圧降下(V)と電流の値(A)を求めよ。
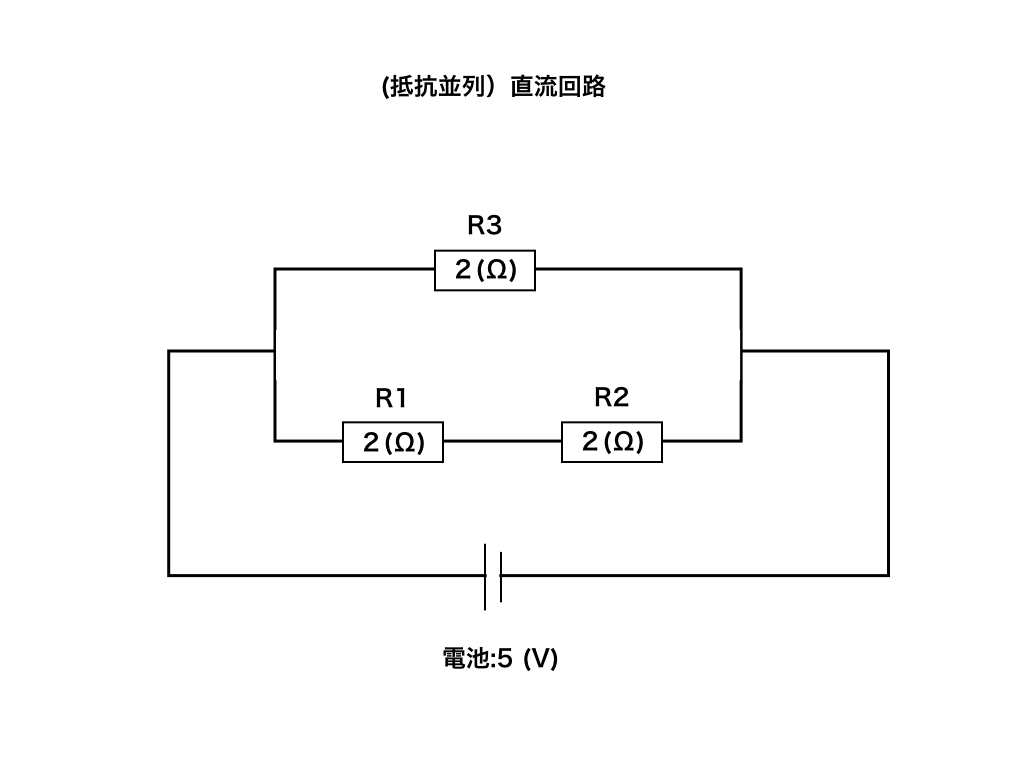
今回はこの基礎レベル2題を使って、キルヒホッフの法則と電気回路の問題の解き方を紹介します。
回答解説
解答1:まずは第二法則で扱った『回路を一周すると電位が0』を用いて解きます。
まず電池の電圧5(V)を確認し、抵抗R1を流れる電流をI(A)電圧降下の値をV(V)とします。
電圧:+5-(V)=0より、電圧降下の値は5(V)
電流:オームの法則より5(V)=I(A)・2(Ω)
よって、I=2.5(A)・・・(答)
解答2:問2は少しだけ複雑ですが、手順は変わりません。
まず《閉じた回路》をさがすと、【電池→抵抗R1→抵抗R2→(再び)電池】という回路を見つけることが出来ます。
ここで第二法則を利用して、\(+5(V)-2\times I_{1}-2\times I_{1}=0\)
従って、$$5(V)=4I_{1} ∴ R_{1},R_{2}を流れる電流は\frac{5}{4}(A)$$
電圧降下もオームの法則を使って、\(V=\frac{5}{4}\times 2 \)\(∴R_{1},R_{2}\)での電圧降下はそれぞれ\(\left(\frac{5}{2}\right)(V)\)
(※:慣れるとここまで丁寧に解かなくても直ぐに答えを出すことができるようになります)
残りはR3です。ここでは【電池→抵抗R3→電池】という並列部分の上側を通る一周を考えます。
従って、
$$電流:5(V)-2(A)\times I_{3}=0より、I_{3}=\frac{5}{2}$$
\(電圧降下:5(V)-V_{3}=0より、V_{3}=5(V)\)
が答えとなります。
キルヒホッフの法則まとめと続編へ
・キルヒホッフの第1法則は「”電流”について、ある点において、Σ流れこむ電流=Σ流れ出す電流」を述べている
・キルヒホッフの第2法則は「”電圧”について、閉回路のΣ起電力=Σ電圧降下」を述べており、回路問題を解くに当たって最重要の考え方になる
・数多く回路の問題を練習して定着させて行きましょう。
・「高校物理・物理基礎の電磁気分野総まとめ!」左の記事にこれまでの電気に関する記事と、磁気(追加中)の記事を集めました。是非ご利用ください。
電磁気分野関連記事へ
〜電流と回路シリーズ〜
第1回:「電流の意味とI=envsの式のイメージを図解」
第2回:「非オーム抵抗の問題と特性曲線の交点が解になる単純な理由」
第3回:「今ココです」
第4回:「コンデンサーや抵抗・その両方が含まれる回路の解き方のコツ」
第5回:「(作成中)」
今回も最後までご覧頂き、有難うございました。
当サイト「スマナビング!」では、読者の皆さんのご意見や、ご感想、記事リクエストの募集をコメント欄にて行なっています。
また、 いいね!・B!・シェア、Twitterのフォロー等をしていただけると励みになります。
・その他のご依頼などに関しましては、お問い合わせページからご連絡下さい。

