
等加速度運動の3公式と投げ上げ運動
<今回の内容>:今回は、鉛直投げ上げ運動をマスターする事を目的に、まず「等加速度運動」とその「重要な3公式」の解説を行い、鉛直投げ上げ運動を取り上げます。
目次(タップした所へ飛びます)
等加速度運動と鉛直投げ上げ運動
・等加速度運動とは?
・等速運動との違い
・等加速度運動の3公式の導出と図形で見る意味
・等加速度運動の練習問題
・鉛直投げ上げ運動と等加速度運動
・最高点の位置と時間を3秒で出せる小技
等加速度運動とは?
読んで字のごとく、「加速度の大きさが常に同じ運動」の事です。
等速運動との違い
等加速度運動は常に一定の加速度で(加速していく/減速していく)運動なのに対して、等速運動は速さが常に等しく運動するものの事です。(=つまり加速度0)
等加速度運動の3公式を図形で導出する
等加速度運動で非常に頻繁に使用する3つの公式があります。
一見ややこしそうですが、図形を使って導く方法を説明するので、理屈と共に導き方を覚えておいて下さい。
そうすれば、ただの公式暗記をせずにすみます。
aを加速度(\(m/s^{2}\))、vを速度(m/s)、xを変位(m)、tを時間(s)として(但し\(v_{0}\)は初速度)
(1)X=v0t+(at ^2)/2
$$x=v_{0}t+\frac {1}{2}at^{2}$$
(2)V=v0+at
$$v=v_{0}+at$$
(3)V^2–V0^2=2ax
$$V^{2}-V^{2}_{0}=2ax$$
(1)の公式の意味:
t秒後の変位xは、\((初速度)v_{0}×t+(加速度)a×1/2×t ^{2}\)で表すことができ、
<図1のVーTグラフ>の斜線の部分の面積(時間×速さ)と同じである事を示しています。
(2)の公式の意味は、「t秒後の速度Vは初速度v0+加速度a×t」と表せ、<図1>のグラフ右端の高さと等しいです。(速度が時間当たりにどれだけ変化するか=加速度a=VーTグラフの傾き)
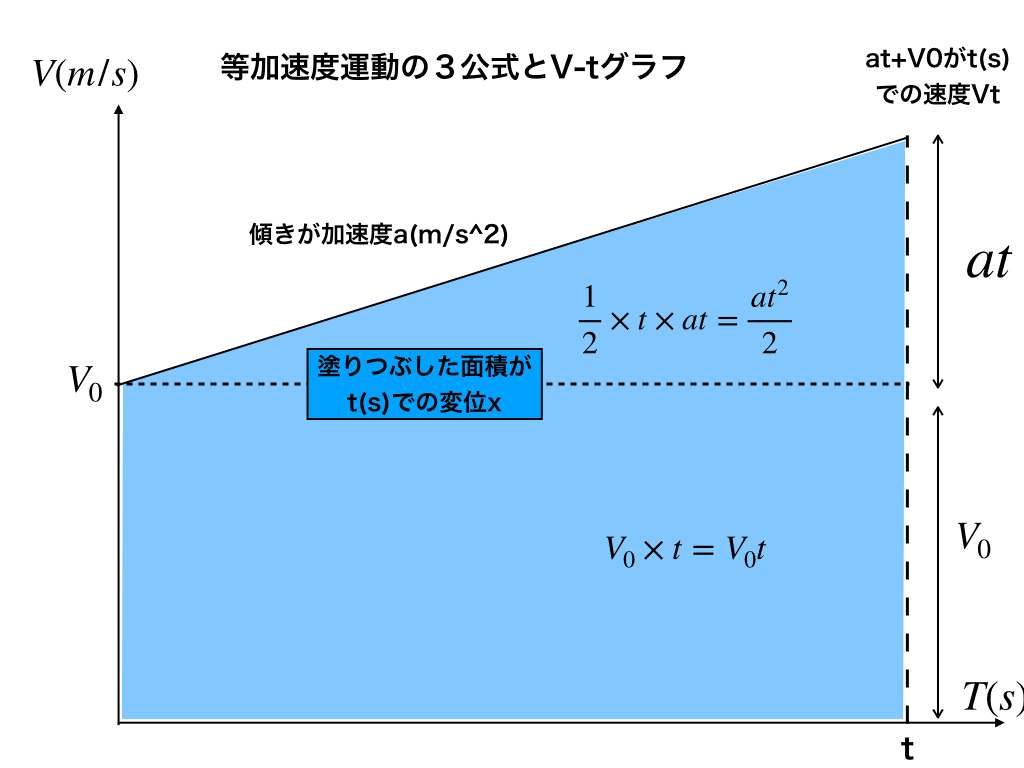
<図1のVーTグラフ>
(3)の公式は、(2)の公式を変形して(1)に代入する事で得られます。
$$\frac {v-v_{0}}{a}=t$$
$$x=v_{0}\left( \frac {v-v_{0}}{a}\right) +\frac {a}{2}\times \left( \frac {v-v_{0}}{a}\right) \times \left( \frac {v-v_{0}}{a}\right) $$
$$x=\frac {vv_{0}-v^{2}_{0}}{a}+\frac {v^{2}-2vv_{0}+v^{2}_{0}}{2a}$$
よって、
$$2ax=v^{2}-v^{2}_{0}$$
等加速度運動の練習問題
摩擦のない床上を物体Aが原点Oをt= 0(s)で
x軸正方向に初速度V0=15(m/s)、
加速度a=ー5(m/s ^2)で通過した。
(1)原点から正方向に最も離れた時間Tとその時の位置Xを求めよ。
(2)速度が10(m/s)になる位置X‘を求めよ。
解答解説
(1)「原点から最も離れた」とあるので、この時正方向の速さは 0です。
従って、\(v=v_{0}+at\)より
0=15+(-5t) t=3(s)//
位置Xは、$$x=v_{0}t+\frac {1}{2}at^{2}$$
より、X=15・3+(1/2)(-5)(3^2)
X=22.5(m)//
(2)「速度」が10(m/s)なので、
\(V^{2}-V^{2}_{0}=2ax\)より、
\(10^{2}ー15^{2}=2(-5)X’\)
X‘=12.5(m)//
鉛直投げ上げ運動への応用
ここでは、「投げ上げ運動」と呼ばれる運動について解説します。
(鉛直)投げ上げ運動とは真上に、ある初速度で物体を投げたときの物体の運動を言います。
これまでは、水平方向の等加速度運動を扱ってきましたが、投げ上げ運動でも重力加速度g≒9.8(m/s ^2)が物体にかかるので、これも一種の等加速度運動と言えます。
従って、等加速度運動の3公式も加速度aの部分を重力加速度gに、変位xを高さhに置き換えるだけで同じ様に使えます。
鉛直投げ上げの3公式
ここでは、鉛直上向きを正として公式を書いておきます。
gを重力加速度(m/s^2)、vを速度(m/s)、hを高さ=変位(m)として
(1)’h=v0t+(ーgt ^2)/2
$$h=v_{0}t-\frac {1}{2}gt^{2}$$
(2)’V=v0ーgt
\(v=v_{0}-gt\)
(3)’V^2–V0^2=2(-g)h
\(v^{2}-v^{2}_{0}=-2gh\)
ここでは重力加速度は軸と反対向きにかかるので、ーgと負の符合が付いていることに注意して下さい。
最高点の高さとその時間を3秒で出すコツ
鉛直投げ上げ運動の他にも斜方投射など、物体の最高点の位置とその時の時間を問われる事が度々あります。
そんな時に知っておくと楽なワザを紹介します!
初速度をv0 、重力加速度をg、最高点をh max、その時の時間をt maxと置くと
h max=v0 ^2/2g
$$h_{\max }=\frac {v^{2}_{0}}{2g}$$
t max= v 0/g
$$t_{\max }=\frac {v_{0}}{g}$$
となります。もちろんこの2式は等加速度運動の3公式から導出出来ます。
「最高点にいる=鉛直上向きの速度が0」と、
\(v^{2}-v^{2}_{0}=-2gh\)より、\(v^{2}=0\)を代入して整理すると、
$$v^{2}_{0}=2gt,t=\frac {v^{2}_{0}}{2g}$$
(∴)$$h_{\max }=\frac {v^{2}_{0}}{2g}$$
「V=V 0ーgt」
のV= 0の場合だから、同様に、gt=V 0
(∴)$$t_{\max }=\frac {v_{0}}{g}$$
導出法と共に頭に入れておくと便利です。
続編(力学シリーズ一覧)へ
引き続き、斜方投射・放物運動と軌道の式の解説記事をご覧ください。
今回も最後までご覧いただき有難うございました。
質問・記事について・誤植・その他のお問い合わせは、コメント欄までお願い致します。

