理想気体のグラフの頻出問題を攻略!
<この記事の内容>:以下のような、
<問題例(解答方法は本編で詳しく解説します)>:次のグラフのうち正しいものはどれか。
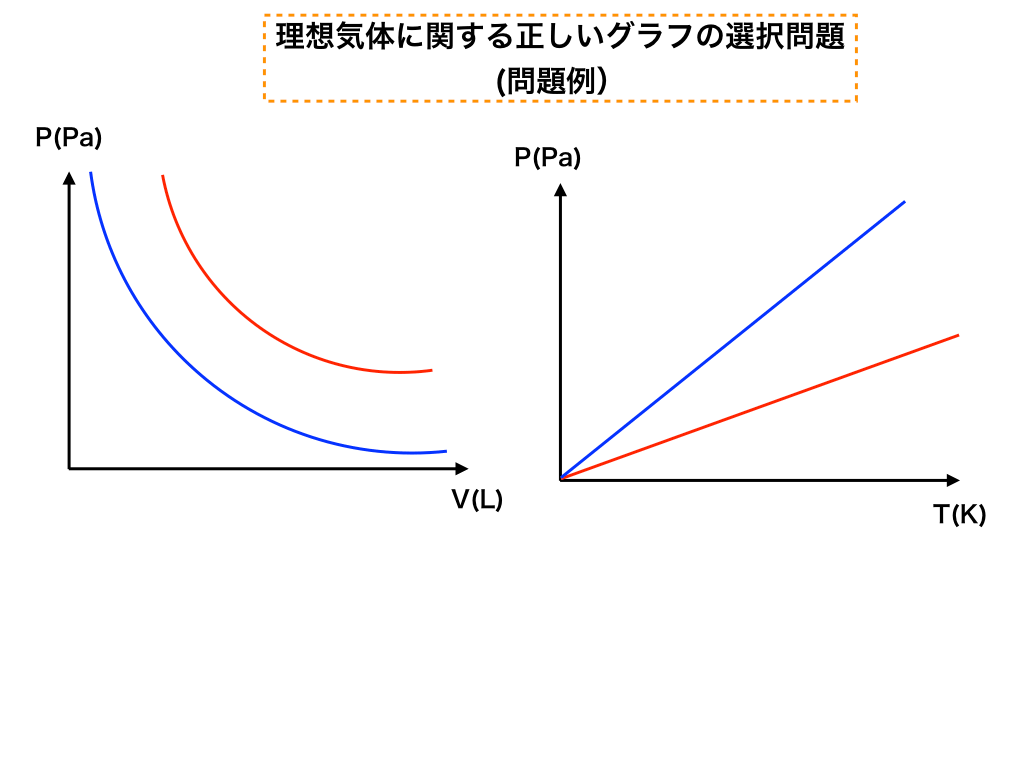
・「理想気体において『PーVグラフ』での\(T_{1},T_{2}\)や、『V-Tグラフ』での\(P_{1},P_{2}\)、『P-Tグラフ』での\(V_{1},V_{2}\)などがそれぞれ並べてあって、正しいものを選ぶ」
という頻出問題が苦手な人を対象に、
・《状態方程式の利用と少しの変形》で確実に正答できるよう、具体的な問題を通して解説しています。
目次(タップした所へ飛びます)
理想気体とP-T/V-T/P-Vグラフ
先に、ボイル=シャルル/ボイル/シャルルの各法則および、《理想気体の状態方程式》の知識を確認したい人は、
>>「状態方程式を0から解説!計算や式の意味ボイル=シャルルの導出など」<<をご覧ください。
圧力Pー温度TグラフとV(体積)の比較
まず縦軸にPressure(P)横軸にTemperature(T)温度を持ってきたグラフを見てみます。
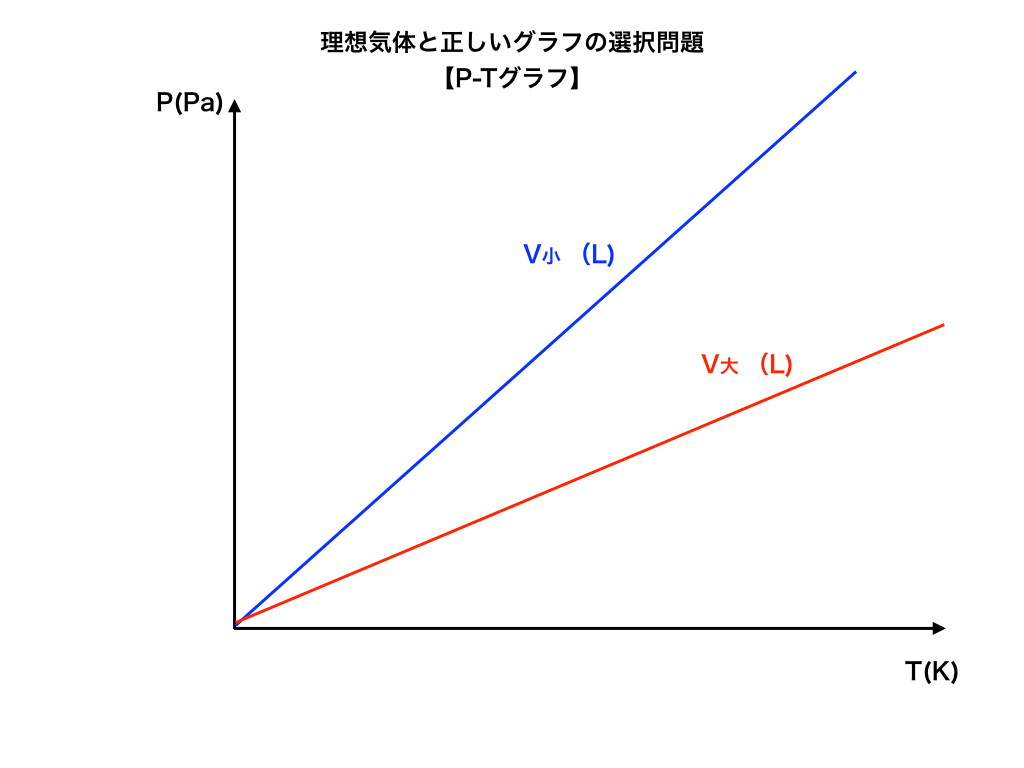
この図の正誤を判定する方法は、”『PV=nRT』を変形するだけ”です。
具体的には”数学のxーy座標”をイメージして、縦軸の”y”の代わりに”P"があり、横軸の”x”の代わりに“T”になっていることから、y=αxのグラフを作るように、P=αTの式へとPV=nRTを動かしていきます。
まず:P=(左辺)
にすると、
$$(右辺)=\frac{nRT}{V}$$となり、nとRは変化しませんから(どちらも定数扱いして)αと置いてみます。
$$P=\alpha \frac{T}{V}$$
上の式から、PとTは比例関係にあることがわかるので、確かに上のPーTグラフは◯。
図中のV1/V2の上下関係の判別法
ところで、”V”の扱い方ですが、問題の図中に\((V_{1},V_{2})\)といった2つ(以上)の直線or反比例の曲線が出てくる場合があります。
その時には『比例関係であることは変わらず意識しながら』、指定された\(V_{大},V_{小}\)を分母に代入してあげることで、
\(V_{大}\)の方が分母が大きくなる
↓
よって全体としてPの値は小さくなる
↓
二本の比例グラフのうち下側が\(V_{大}\)と判断できる。と言う風に解いていくことが出来ます。
(一例です。詳細は以下の問題編にて。)
圧力P-体積VグラフとT(温度)の比較
次に、縦軸にPressure(P)横軸にVolume(V)体積のグラフです。
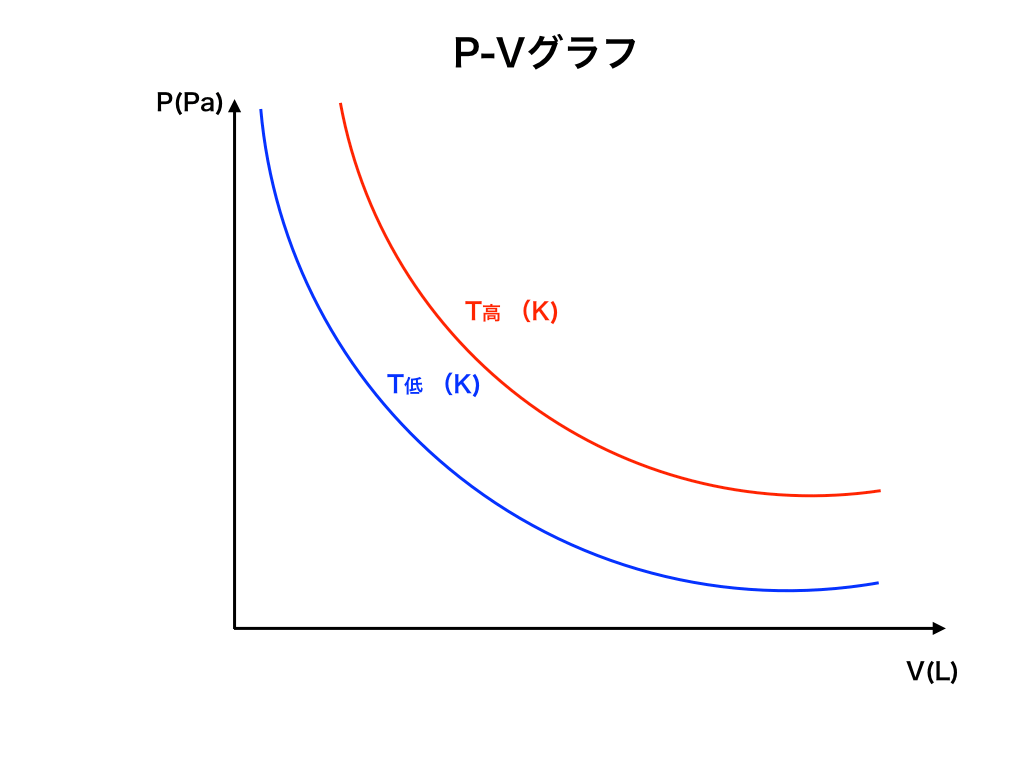
同様にPV=nRTより、$$P=\frac{nRT}{V}$$
nとRはこの場合も(どちらも定数扱いして)αと置き、
$$P=\alpha \frac{T}{V}$$
上の式から、PとVは反比例の関係にあることがわかるので、確かに上のPーVグラフは◯です。
Tの扱い方
また、図中の\(T_{1}、T_{2}\)については、上で紹介した「P-Tグラフ中のV1、V2」の判定法と同じように進めます。
体積Vー温度TグラフとP(圧力)の比較
3つ目は、縦軸にVolume(V)体積、横軸にTemperature(T)温度のグラフを見てみましょう。
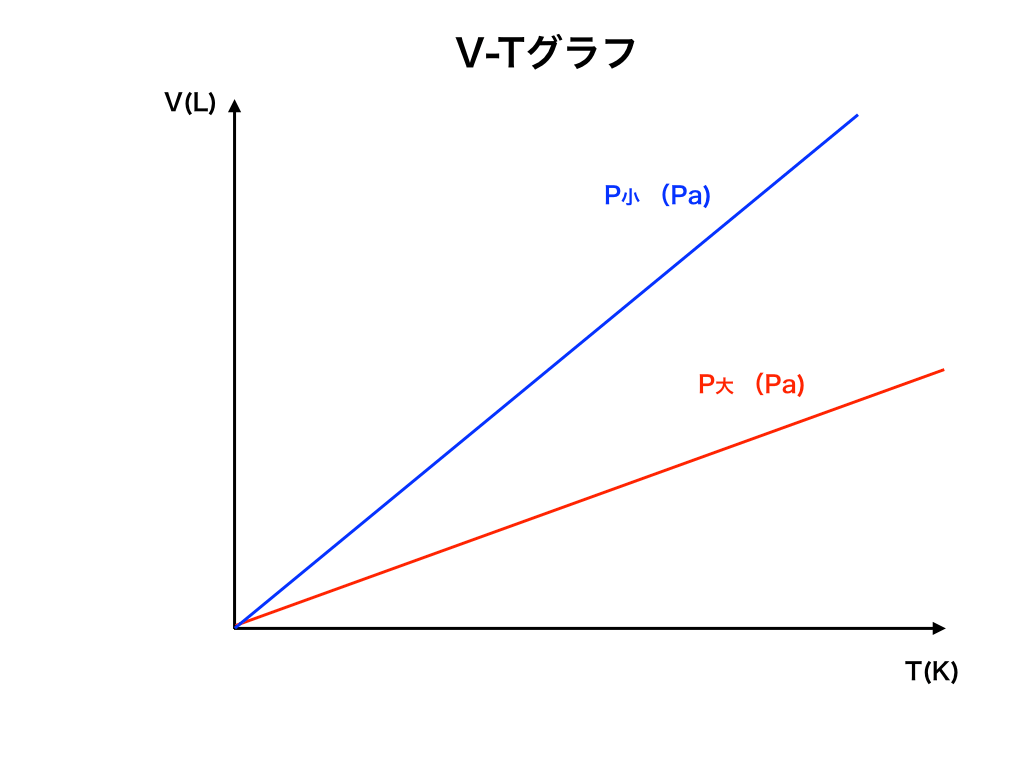
もう立式の方法にも慣れて来たのではないでしょうか?(3回目です。)
PV=nRTより今度はVを(左辺)に残して、$$V=\frac{nRT}{P}$$
nとRをαと置き、
\(V=\alpha \frac{T}{P}\)
上の式から、TとVは比例の関係にあることがわかるので、確かに上のVーTグラフは◯。
Pの扱い方
図中の\(P_{1}、P_{2}\)もこれまで通りの方法で◯×を調べます。
比例/反比例の考え方で正しいグラフを選ぶ方法【問題編】
では、ここからは上のグラフを全て合わせて、正しいものを選ぶ”具体的な”例題を紹介します。
問題:6つのグラフから正しいものを選ぶ
以下の(a)〜(f)までの六つのグラフから、正しいものを選んで答えよ。ただし、\(T_{1}>T_{2},P_{1}>P_{2},V_{1}>V_{2}\)とする。
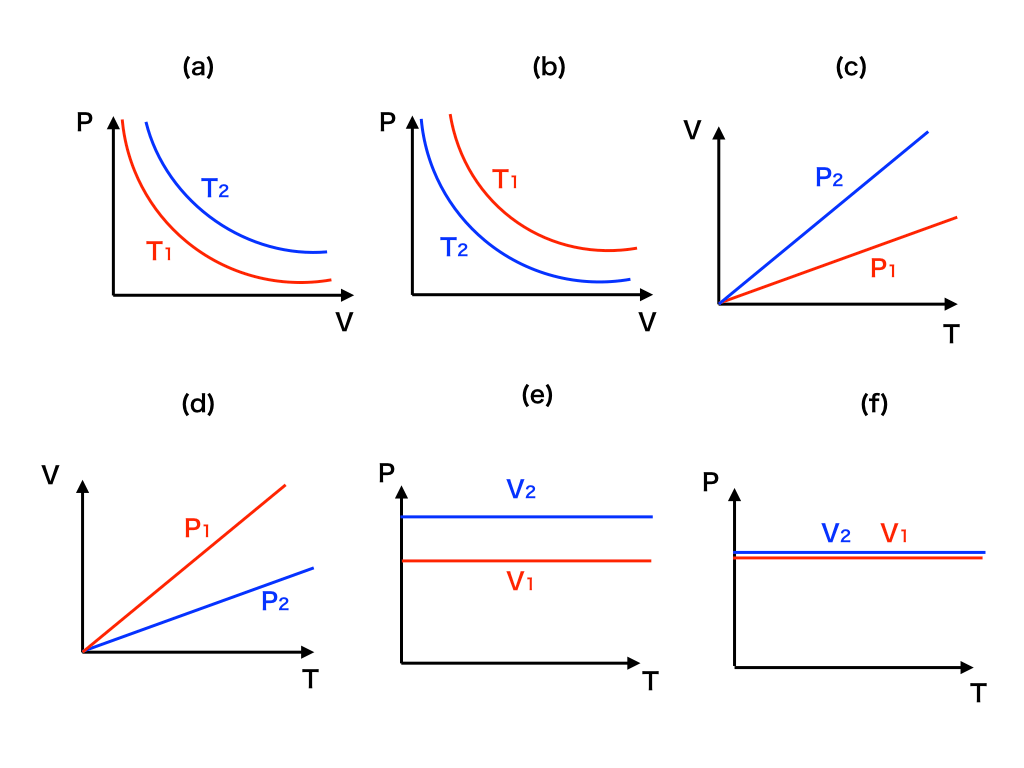
センター試験、2次試験などでよく見るタイプの問題です。
解説と式変形の方法・考え方
ではここからは、(a)〜(f)まで、一つ一つ立式して◯×を判定していきましょう。
反比例になっている場合
(a)と(b):反比例のグラフになっています。
実際に縦Pー横Vの軸に合わせて式を立てて、定数部分をαとおいていくと、$$P=\frac{nR}{V}T⇔P=\frac{\alpha}{V}T$$
従って反比例である点は(a),(b)共に正解です。
次に図中の\(T_{1},T_{2}\)の上下について考えます。
すると、\(T_{1}>T_{2}よりT_{1}\)の方がPを大きくするので、正解は(b)・・・(答)。
比例関係の場合
(c)と(d):先ほど上で解説したV-Tグラフです。pv=nRTから変形することで、$$V=\alpha \frac{T}{P}$$(詳細は上の項を参照してください)。
あとは\(P_{1}>P_{2}\)を考慮するとPが大きいほど分母が大きくなり、Vが小さくなるので\(P_{2}\)が上に来る(c)が◯です。
値が一定となっている場合など
(e)と(f)は共に値が一定になっています。
縦P-横Tを見るとこれは本来、比例関係にないといけない:$$P=\frac{nR}{V}T⇔P=\frac{\alpha}{V}T$$ので、この時点で両方とも×です。
従って、(a)~(f)のうち、正しいグラフは (b)、(c) ・・・(答)
解法の4stepまとめと理論化学:気体の記事へ
この様に、グラフがたくさんあり、軸も違う上に引かれた線も2本以上あるような「一見どこから手を付けていいかわからない」問題ですが、
step1:状態方程式を変形
↓
step2:軸の2つと引かれた線の「3つ」以外を定数とおき、式を作る
↓
step3:比例・反比例を(step2の式)で判定
↓
step4:図中の曲線/直線の大小(上下関係)は変形した式から読み取る
この4つのstepで必ず正答できるので、何度か復習をしながら解法を身に付けてみてください。
気体シリーズ一覧
気体分野・関連記事
(NEW!):>>「気体・溶液分野の記事まとめ」<<
>>「物質の三態とグラフ・状態変化」
学習・受験メディア『スマナビング!』では、読者の皆さんの「ご意見、ご感想」をコメント欄にて募集しています。
(※):現在、個々の問題のご質問については時期的に対応できない場合がございます。
(誤植の指摘や、ご感想は引き続き募集しています。)
・また、お問い合わせ/ご依頼等、その他のご連絡については、【運営元ページ】よりお願いいたします。

