
ドップラー効果応用編
前回のドップラー効果の解説と公式の導出に続いて、今回は風が吹いていたり、音を反射する反射板が設置されているような”複雑な場合の対処法”を解説していきます。
前回の記事を読んでいない人・復習したい人は→「ドップラー効果(1)基礎編」を先にご覧ください。
目次(タップした所へ飛びます)
ドップラー効果の公式
ここでは、今回の記事の理解に最低限必要な公式を紹介します。
\(V=f\lambda \)
$$f'=f\times \frac {V\pm v_{o}}{V\pm v_{s}}$$
ただし、V(m/s)は波の速さ、f(Hz)は振動数、λ(m)は波長、
\(v_{s}(m/s)\)を音源の速さ、\(v_{o}(m/s)\)を観測者の速さとする
風が吹いている時のドップラー効果
これまでのドップラー効果の式では無風状態を条件にしていました。ここからは、風の影響も考えて解いていきます。
風には、追い風と向かい風の2種類があり、音源から観測者へ向かう風が追い風;その逆観測者から音源への風が向かい風となります。
風の速さはw(m/s)で表します。
風速によって変化するのは音速V(m/s)
音は空気によって伝わるので、風が吹く=空気が動く=音速Vが±w(m/s)変化することを意味します。
従って、「風が吹いている」と問題文にあれば、
ドップラー効果の基本式$$f'=f\times \frac {V\pm v_{o}}{V\pm v_{s}}$$
のV(分母・分子両方)に±wを加えて下さい。
例題で具体的にみていきます。
(例題1)風とドップラー効果
今、<図1>の様に音源がf(hz)の音を出しながら、静止している観測者の方へ速さv(m/s)で近付いている。
この時の音速をV(m/s)とし、風が音源から観測者の方向にw(m/s)で吹いている。
観測者が聞く音の振動数f’(Hz)を求めよ。
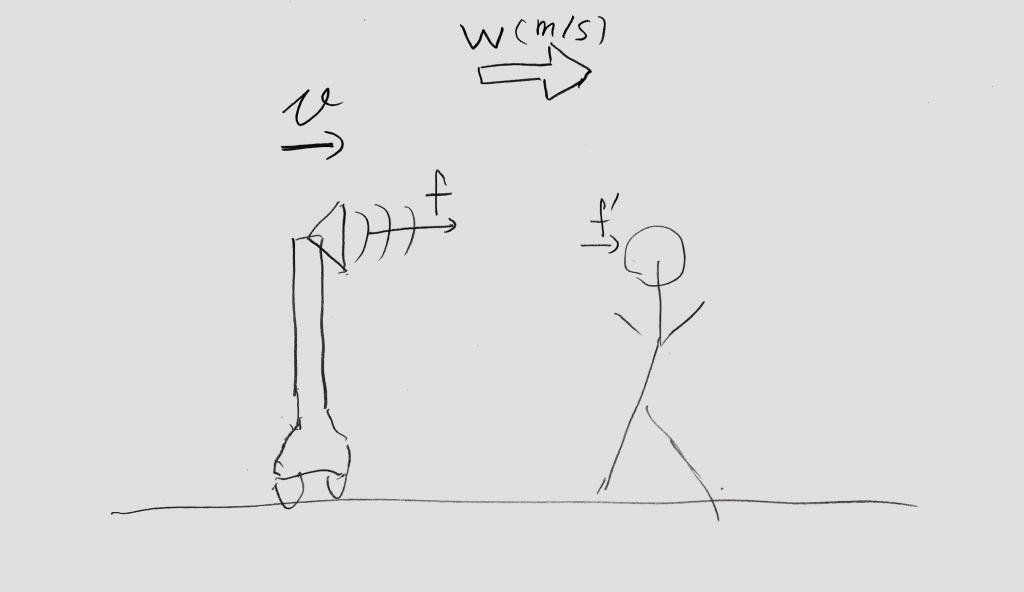
<図1>
(解答解説1)
二段階で考えていきます。(立式は一回)
(1)風が音源→観測者へw(m/s)で吹いているので、基本式の分母/分子の音速V(m/s)をV +w(m/s)に書き換えます。
(2)次に前回の記事で解説した様に音源が動き、観測者に近づくので,
分母のV(m/s)から\(v_{s}\)を引きます。
(音源が近づく→fが大きくなる→分母を小さくする)
よって、(1)、(2)を合わせて、f’は、
$$f'=f\times \frac {V+ w}{V+w-v_{s}}$$
反射板が設置されている時のドップラー効果
反射板とはその名の通り、音を反射するものです。ここでは、無風状態であるとします。
反射板の2つの役割
反射板は音源から音を観測し、それを反射すると言う「観測者」と「音源」の2つの役割を同時に担います。
音源/観測者/反射板が動く時に観測者が聞く振動数
(例題2)
今、<図2>の様に音源 観測者 反射板 の順に並んでいる。
音源、観測者、反射板の3つ全てが右向きに動き、
それぞれの速度を\(v_{s}(m/s)、v_{o}(m/s)、v_{r}(m/s)\)とする。
音速がV(m/s)で風が吹いていないとするとき、
観測者が音源から聞く音の振動数\(f_{so}(Hz)\)と、観測者が反射板から聞く音\(f_{ro}(Hz)\)を求めよ。

<図2>
(解答解説2)
まずは、音源から直接観測する音の振動数\(f_{so}(Hz)\)を求めます。
ドップラー効果の基本式より、音源も観測者も動くから、
$$f_{so}=f\times \frac {V-v_{o}}{V-v_{s}}$$
(この式が直ぐに作れなければ一旦→ドップラー効果/音源と観測者の復習←をご覧下さい。)
次に反射板から観測者が聞く音の振動数ですが、これを求めるには二段階の計算が必要です。
まず反射板を観測者と考えて、音源から受け取る
$$音の振動数f_{sr}=f\times \frac {V-v_{r}}{V-v_{s}}$$
次に反射板を音源と考えて観測者が受け取る
$$音の振動数f_{ro}=f_{sr} \times \frac {V+v_{o}}{V+v_{r}}$$
$$よって、f_{ro}=f\times \frac {V-v_{r}}{V-v_{s}}\times \frac {V+v_{o}}{V+v_{r}}$$
となります。
このとき真ん中の観測者は左右から異なる振動数の音を聞きます。
この振動数の差が小さい時「うなり」を聞くことになります。
続編(斜め方向のドップラー効果へ)
続編アップしました。
ドップラー効果第1回:「ドップラー効果の仕組みと公式の導出法」
ドップラー効果第2回:「反射板や数が吹いている時のドップラー効果」今ここです
ドップラー効果第3回:「斜め方向のドップラー効果と演習問題」
今回も最後までご覧いただき有難うございました。
お役に立ちましたら、シェア&当サイト公式Twitter(@linkyjuku_tweet)のフォローをお願いします!
質問・記事について・誤植・その他のお問い合わせはコメント欄までお願い致します。

