
累積分布関数とは
<この記事の内容>:統計学で登場する「累積分布関数」を具体例(問題)をまじえながら、その意味や確率関数との関係などを解説しています。
<ここまでの統計学>:「0からの統計学/データ分析」
目次(タップした所へ飛びます)
累積分布関数とは
先に定義を書いておきます。
累積分布関数の定義
確率密度関数をf(x)とする時、
P(-∞<X≦x)=F(x)
$$F(x)=\int_{-\infty}^{x}f(u)du $$
上の式では連続型の確率分布の場合を書きましたが、離散型でも同様です。
これはどのような意味を持つのでしょうか。
確率密度/質量関数との関係
簡単に説明すると、確率密度関数f(x)において、【xという値以下をとる確率】を関数として表したものが累積分布関数:F(x)と言えます。
積分して求まる関数=(累積)分布関数
もう少し定義式を見ていくと、f(u)を積分区間を\(-\infty→x\)としています。
これは上述したように、確率密度関数の面積を”x”という値まで求めている(=すなわちF(x)という関数は、xまでの確率を累積(=積み重ねたもの)した値を表している)という意味です。
少し抽象的ですね。。実際に具体例を用いて問題を解きながら意味を理解していきましょう。
累積分布関数の問題とその解き方
ここでは、連続型の確率密度関数を決定→累積分布関数を求め→グラフ化する、という一連の流れを解説していきます。
定着用例題
いま、確率密度関数f(x)が次のように定数aを用いて表されている。
$$
f(x) = \begin{cases}
0 & (x<0) \\
ax & (0\leq x<2) \\
2a & (2\leq x\leq4) \\
0 & (4< x)
\end{cases}
$$
(1):この時、aの値を求めよ。
(2):f(x)の累積分布関数を求め、そのグラフをかけ。
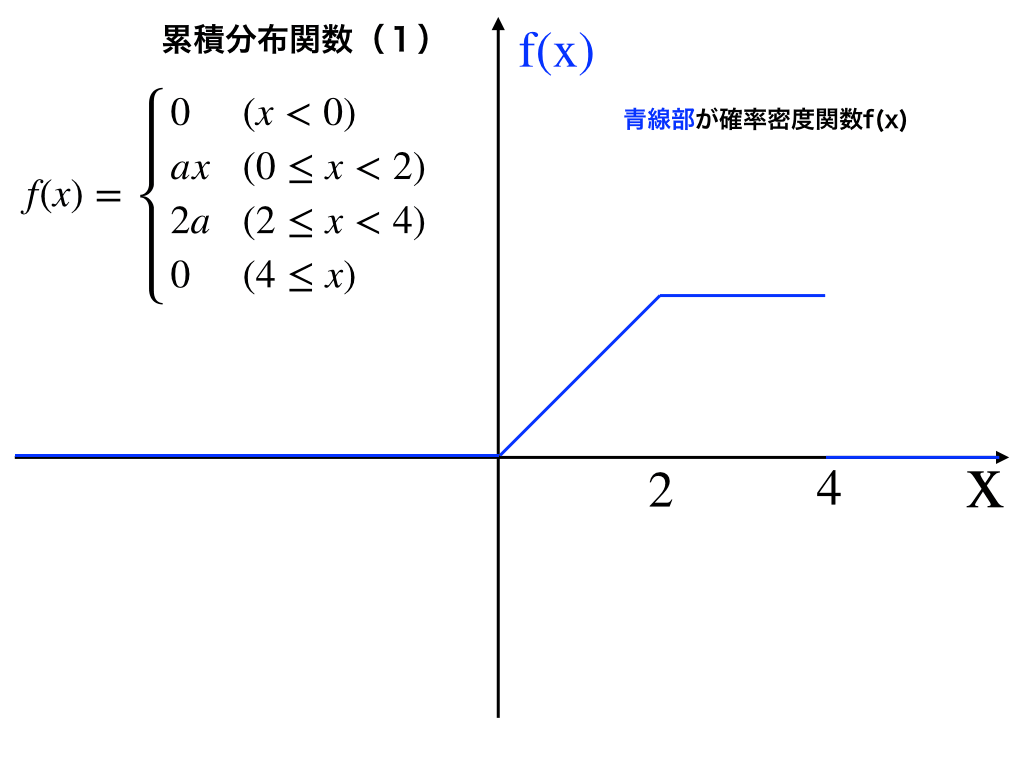
解答解説:全確率=1を用いる
$$\int_{-\infty}^{\infty}f(x) dx=1$$
上の確率密度関数のうち、x<0と4<xの確率は0となっているので、【f(x)=axとx軸で囲まれた面積】+【f(x)=2aとx軸で囲まれた面積】が全確率=1になるはずです。
そこで、
$$1=\int_{-\infty }^{0}0 dx+\int_{0}^{2}ax dx+\int_{2}^{4}2a dx+\int_{4}^{\infty}0 dx$$
$$(右辺)=[\frac{ax^{2}}{2}]_{0}^{2}+[2ax]_{2}^{4}$$
これを計算すると、a=1/6・・・(1)と求まります。
$$
f(x) = \begin{cases}
0 & (x<0) \\
\frac{x}{6} & (0\leq x<2) \\
\frac{1}{3} & (2\leq x\leq4) \\
0 & (4< x)
\end{cases}
$$
累積分布関数とグラフを求める(場合分け)
つぎに、累積分布関数をx<0,0≦x<2,2≦x≦4,4<xの4通りに場合分けして計算を進めます。
定義式より、
(一):x<0のとき$$F(x)=\int_{-\infty}^{x}0du$$
(二):0≦x<2,のとき$$F(x)=\int_{-\infty}^{0}0du+\int_{0}^{x}\frac{u}{6}du$$
(三):2≦x≦4,のとき$$F(x)=\int_{-\infty}^{0}0du+\int_{0}^{2}\frac{u}{6}du+\int_{2}^{x}\frac{1}{3}du$$
(四):4<x,のとき$$F(x)=\int_{-\infty}^{0}0du+\int_{0}^{2}\frac{u}{6}du+\int_{2}^{4}\frac{1}{3}du+\int_{4}^{x}0du$$
(一)〜(四)を計算すると
$$\mathrm{F(x)}=0(x<0)$$
$$\mathrm{F(x)}=\frac{x^{2}}{12}(0\leq x< 2)$$
$$\mathrm{F(x)}=\frac{x-1}{3}(2\leq x\leq4)$$
$$\mathrm{F(x)}=1(x>4)$$
結果的に、グラフは以下のようになります。
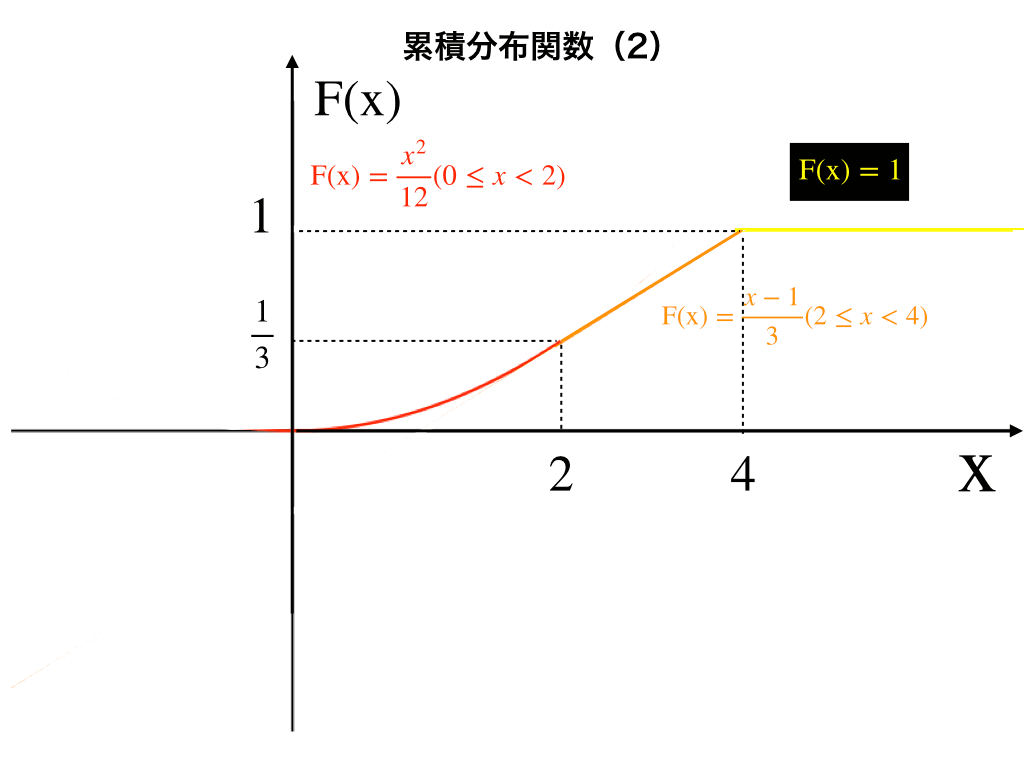
ここで、縦軸が0から1までの確率となっています。
F(x)を微分すると確率密度関数f(x)に、逆にf(x)を積分すると累積分布関数となる関係が理解できたでしょうか。
累積分布関数まとめ
・全確率を利用し、密度関数を決定する方法や
・密度関数を場合分けして積分し、累積分布関数を求める流れ
を確認しておきましょう。
統計/機械学習の続編記事へ
最後までご覧いただき,有難うございました.
【受験・学習メディア】:「スマナビング!」では,読者の皆様からのご感想を募集しています。
ぜひコメント欄までお寄せください。
(※:個々の問題・証明の質問には対応出来ない場合があります。)
・その他の「お問い合わせ/ご依頼/タイアップ他」に付きましては【運営元ページ】より、ご連絡下さい。

