image by Schnelliboy
今回のテーマは「ベクトルの一次独立」です。
このあたりから本格的に分からない!と言う人が出て来るので、さらに丁寧に解説して行きます。
目次(タップした所へ飛びます)
そもそも一次独立ってなんなんだ!?言葉の意味も分からん、、、
一次独立というものが良く分からずベクトルに苦手意識を持ってしまう人が沢山います。
しかし、最低限のベクトルの知識があれば一次独立自体はとても単純です。
ベクトルとは
簡単にベクトルのおさらいをしておきます。ベクトルは、これまで学んできた数(スカラーと言います)と異なり、「向き」と「大きさ」を持っています。
今から説明する3つの事は一次独立を理解するにあたって大切な事なので、ここでも解説しますが
それぞれ詳細な解説ページを作ってあるので、ぜひそちらも参照して下さい!
そして、今回の内容と関わりの大きいものとして、
(1)零(ゼロ)ベクトル
(2)ベクトルの足し算、
更に、一次独立の定義にかかわる重要な事として
(3)ベクトルの成分表示が挙げられます。
零(ゼロ)ベクトルとは
その名の通り、大きさ=長さが0のベクトルの事です。
ベクトルの足し算
ベクトルの足し算はスカラーの足し算と異なります。「向き」を持っている為です。
ベクトルA +ベクトルBは、ベクトルAの終点(矢の先)をベクトルBの始点にくっつけて、
ベクトルAの始点を始点として、ベクトルBの終点を終点とするベクトルで表されます。
更に詳しくは、『ベクトルがさっぱり分からない!』という人向けに書いた、「はじめから教える数学Bベクトル入門第1回」をご覧下さい。
ベクトルの成分表示
ベクトルには、図的に表すだけでなく、その「向き=傾き」を(x、y)の様に表すことが出来ます。下の図をご覧下さい。
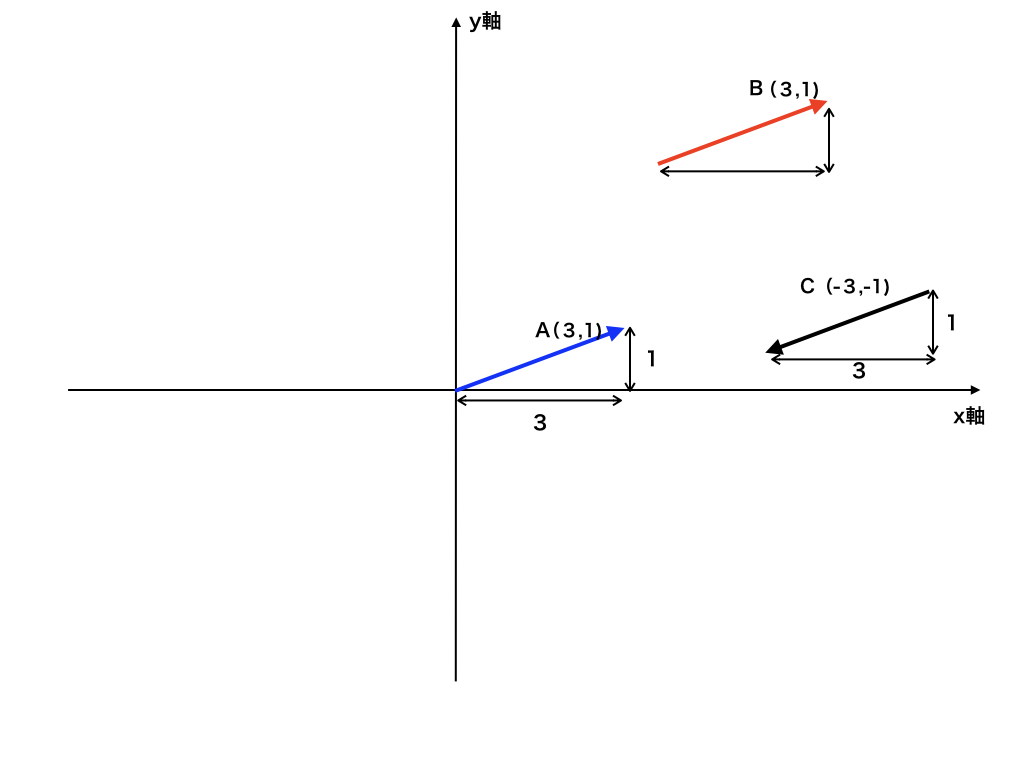
図の様に、(3、1)などが青、赤、黒のベクトルを成分表示した例です。
ベクトルの成分表示については、「ベクトルの成分表示の仕方と成分表示での計算」を参照して下さい。上の2記事とこの記事で一次独立の意味と定義は理解できます。
後は、一次独立を使う(こちらの方が大変です)ことができる様になる為に「ベクトル問題に必須の「係数の和が1」になる条件と理由」と「位置ベクトルって何?そしてベクトルの分解」の2記事の知識があれば「使いこなす」こともできる様になります。
1次独立とは何か
先に書いてしまうと、「一次独立」とは、
「 同一平面上にある2つのベクトルAとBは共に0ベクトルで無く=つまり長さがあり、かつ互いに平行でない関係である」状態を指します。
この時「 AとBは一次独立である」と言います。「一次独立」などと聞くと難しく捉えがちですが、意味はこれだけなのです。
一次独立の定義(平面)
もう少し詳しく一次独立の定義について解説しておきます。(難しく感じたら飛ばしてもらってokです)
平面(2次元)での一次独立の定義は、2つのベクトルの係数がそれぞれ0の時のみ、ベクトルの足し算の結果が0ベクトルになる。
(つまりベクトルを足し算した結果、元の位置にいる)ということです。
要するに2つのベクトルが0以外の係数を持った場合、足し合わせたものが元に戻る事は決して無い。
具体例の方が分かりやすいと思います。
$$\vec {a}=( 2,1) ,\vec {b}=( 1,3) $$
この二つのベクトルabの係数を色々変化させて、$$k_{a}\vec {a}+k_{b}\vec {b}=\vec {0}$$
になる係数の組(ka,kb)を探してみて下さい。$$但し、(k_{a},k_{b})=(0,0)以外で$$
・・・おそらく一生見つからないと思います。これが、上に書いた太字部分の「一次独立の定義」の意味です。
一次独立の定義(空間ベクトル)
空間(3次元)ベクトルの場合の定義は、単にベクトルが2つから3つに変わっただけです。
3つのベクトルの係数がそれぞれ0の時のみ、ベクトルの足し算の結果が0ベクトルになる。
少し難しい話が続きました。
まとめると、「係数が全て0」の場合以外で、各ベクトルの係数をどう変化させても足して0ベクトルにならなければ、それらのベクトルは一次独立している。
できればこの定義を理解しておいたほうが良いです。分からなくなったら、先ほどの具体例を思い出して下さい。
さて、上でも書きましたが、むしろ大切な事はこの一次独立の性質をどの様に使うのかです。
一次独立の使い方
同一平面上にあるどんなベクトル(ここではVとします)も、一次独立な2つのベクトル(AとBとします)の和で表すことができて、その場合のAベクトルとBベクトルの係数は一通りしか無い。
要するに、一次独立の性質より例えば(V=s A +tB)とあらわすならば、ベクトルA,Bの係数の組(s、t)は1組しか無い。
(1)この「1組しか無い」事を利用して、Vを2通りのAとBの和で表し
(2)係数が同じ事から係数比較をして
(3)連立方程式を解くことによって(s、t)を求め
(4)V=s A +tBに代入する事でVを AとBで表して、問題を解いて行きます。
これだけでは、??な人が沢山いると思うので、実際にこれから色々な問題を見て行きます。
一次独立の使い方を問題を使って理解しよう
「係数が1組しか無いという意味」問1-1
一次独立なベクトルAとBがある時、下の条件を満たす(s、t)の値を求めよ。
(s+5)A +(t-2)B=3 A +B
(ヒント)一次独立な2つのベクトルで表されたベクトルの係数は1組しか無い!
(解答:問題1)
AとBは一次独立であるから、左辺=右辺より両辺の AとBの係数は一致する。
(理由:左辺=Vベクトルとすると、<等式で結ばれているので>、右辺もVベクトルである。
同じVベクトルを同じベクトルAとBで表しているので、その場合のAベクトルとBベクトルの係数が異なったらおかしいですよね)
従って、両辺の係数を比較すると
s +5=3
tー2=1 より、(答):(s、t)=(ー2、3) //
問1-2
一次独立なベクトルAとBがある時、下の条件を満たす(s、t)の値を求めよ。
(sー2) A +(tー5)B=2A
(ヒント)
問一とやる事は同じです。右辺にBベクトルが有りませんが、こういう時は係数 0と考えて、 (右辺)=2A +0B として係数を比較します。
解答:問1-2
AとBは一次独立より、両辺の係数を比較すると、
sー2=2
tー5=0 だから、 (答):(s、t)=(4、5)//
ここまでで少し意味がわかってきたでしょうか?「同一のベクトルを2通りに表せば、その2通りの係数は一致する」
極々自然なことを言っている訳です。
本当に係数はただ一通りしかないのか?証明しましょう
感覚的には当然そうなるはずと思えるようになってきたでしょうか?
証明してみましょう。
(問):一次独立なベクトル AとBが有る時、s A +tB=s‘ A +t’B ⇒ s=s‘ かつ t=t’ である事を示せ。
・・・
2通りに表された一次独立なベクトルの和の係数が一致する証明
ベクトル AとBは一次独立で、
s A +tB=s‘ A +t’B・・・#1だから、
変形すると、(sーs’) A=(t‘ーt)B・・・#2
もしs≠s‘と仮定すると、
A={(t‘ーt)/(sーs’)}B ・・#3
#3の時、t=t‘ならば A=0・B となり Aが 0ベクトルに成るので AとBが一次独立、つまりA≠0に反する。
又、t≠t‘ならば{(t‘ーt)/(sーs’)}=k(kは実数)とおくことができ、 A=kBとなって AとBは平行になるから、この時も AとBが一次独立に反する。
従って仮定に反するから、s=s‘
ここでs=s’と#2を合わせると
0・ A=(t‘ーt)B ⇔0=(t‘ーt)B
AとBは一次独立だから、B≠0
よって、
(t‘ーt)=0 ⇔ t‘=t
従ってt=t’
以上より題意は証明された。//
特に最後の証明問題を何も見ずに出来るようになれば、一次独立についてもう悩む事は無いと思います。
最後に実践問題を用意しました。一次独立がしっかり理解できた人は自力で、まだ疑問点が残る人は図と解答を読んでどんな形で問題が出るのか確認して下さい。
ベクトルの一次独立の応用
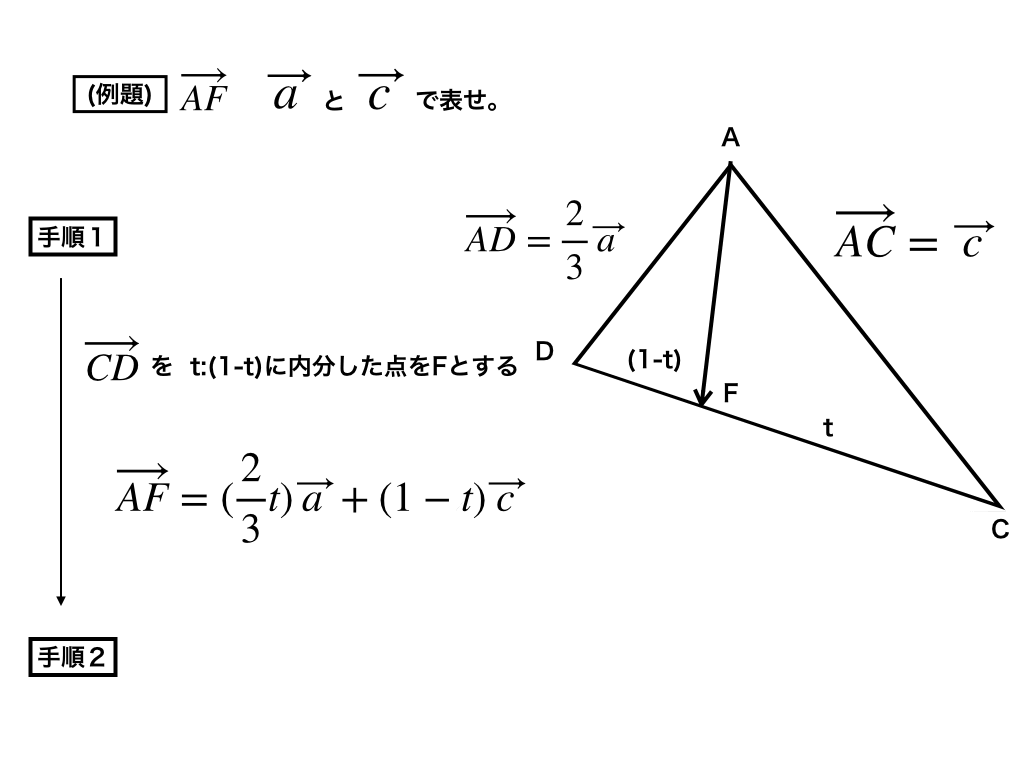
(例題)三角形ABCの辺ABを2:1に内分した点をD、辺ACを1:1に内分した点をEとして、BE、CDの交点をFとする。
この時ベクトルAFをベクトルAB(=ベクトルaとする)とベクトルAC(=ベクトルcとする)で表せ。
・・・例題の文章で嫌になっている人も居ると思うので下の図4で解答、解説を行います。
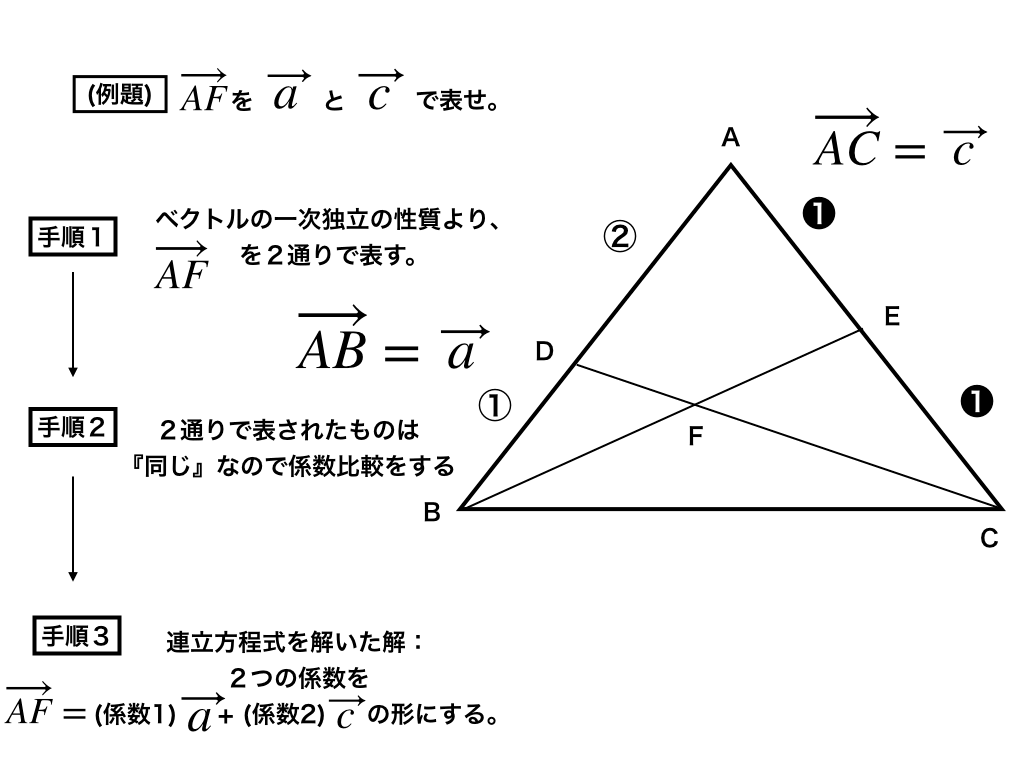
<図4>
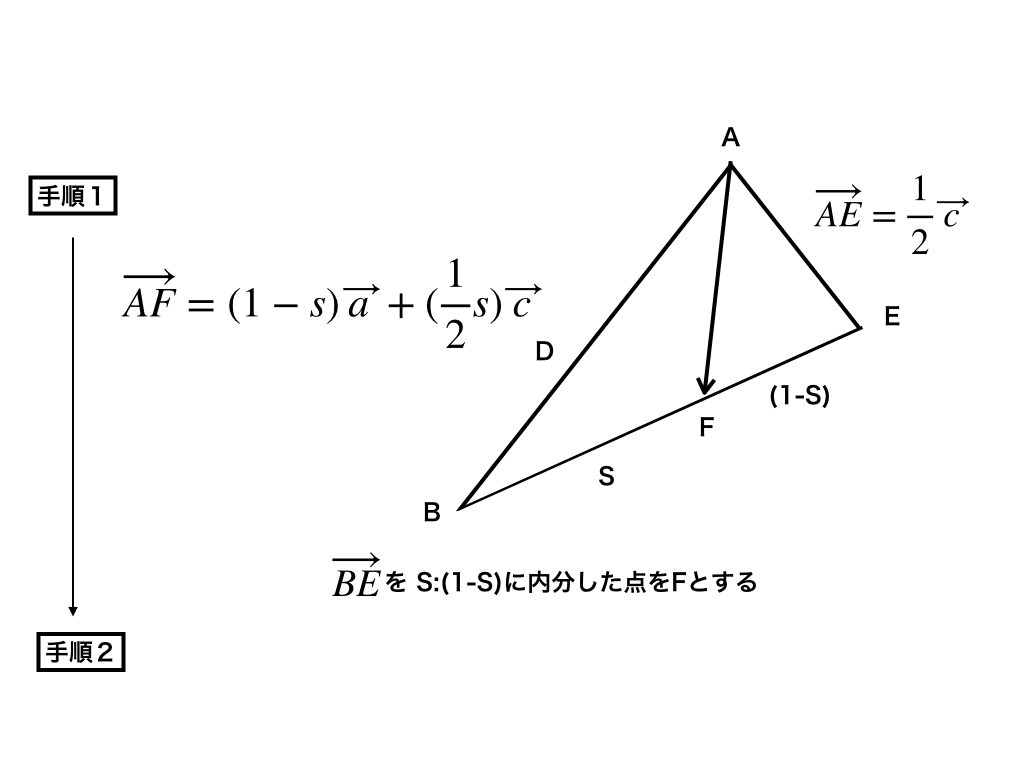
手順1:「ベクトルの一次独立」の性質よりAFを2通りで表す。
↓
手順2:2通りで表したAFは同じものなので「係数が同じ」より、係数比較する。
↓
手順3:係数比較したものを連立してs、tを求めてベクトルAF=aベクトルとcベクトルの係数に代入する。
順を追って説明します。この問題は、よく「交点の位置ベクトル」と言う範囲で頻出のタイプです。
初めて解く人にはややこしいですが、慣れるとただの計算問題になります。
手順1:問題はベクトルAFを書け。となっています。どんなベクトルも一次独立な2つのベクトルの和で表す事ができ、その2つのベクトルの係数はただ一通りしかないのでした。という事は、
ベクトルAFを二通りの2つのベクトルの和で表せればベクトルの係数は一致するので、2つの文字で二通りの式が出来る事から連立方程式を解く要領で係数を求める事が出来ます。
したがってベクトルAFを2つのベクトル、ベクトルAB(aベクトル)とベクトルAC(cベクトル)で表す方法を2通り考えて見ましょう。
ここで知っておくべき公式を紹介しておきます。
ベクトルの内分公式
三角形ABCがあった時、BCを1:2に内分した点をDとする。
この時、ベクトルAD=(2/3)AB+(1/3)ACと表すことができます。
<図5>を見てください。
この様に内分した点の左右での比(ここでは1:2)をクロス(たすきがけの要領です)して足したものとして、内分点を表すことができます。
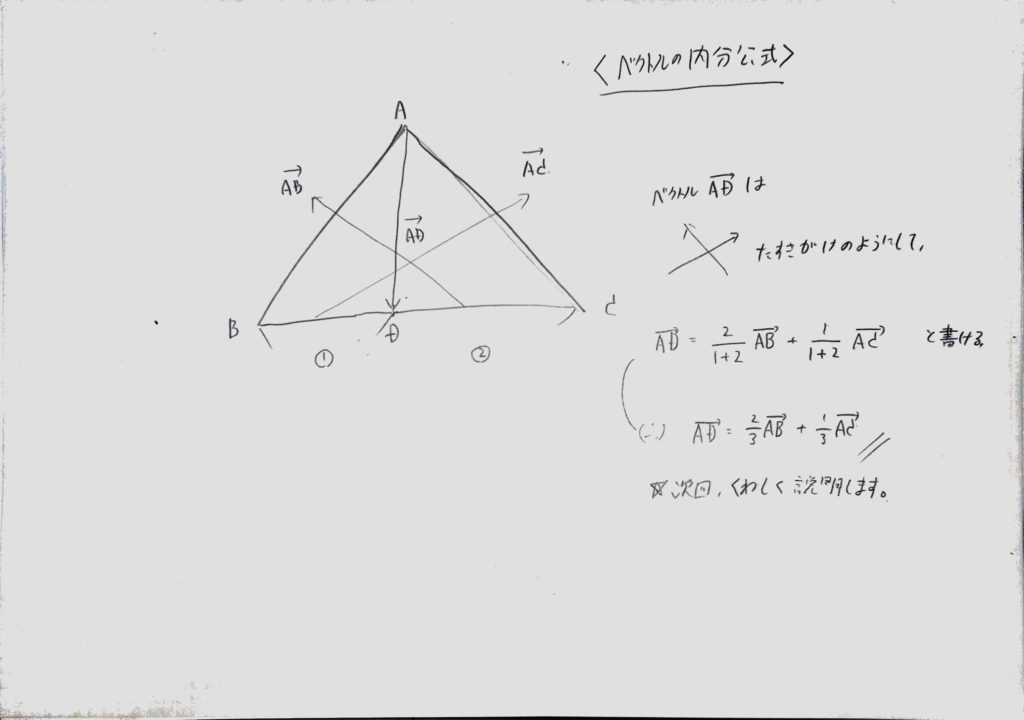
<図5>
では手順1に戻ります。
ベクトルの内分公式より、BF:FEとDF:FCが分かれば、クロスしてベクトルAFを2つ求める事が出来ます。
が、二つの比が分かりません!こう言う時は、なんでもいいので適当な文字で勝手に比を置いてしまって良いです。
但し、必ず比を足したら1になる様に設定して下さい。<図4>でもS:(1−S)とt:(1ーt)と置いていますが、どちらも足して1になりますね?
何故線分を内分した点の比の和が1になるかはこの記事→「係数和1の法則の意味と理由」をご覧下さい。
手順2
ベクトルAFが、内分公式より2通りに表せました。ベクトルAFは一次独立な2つのベクトルaとcで表しているので、当然同じものになるはずです。
と言う事は、先程から述べている様にベクトルaとベクトルcの係数は同じになります。
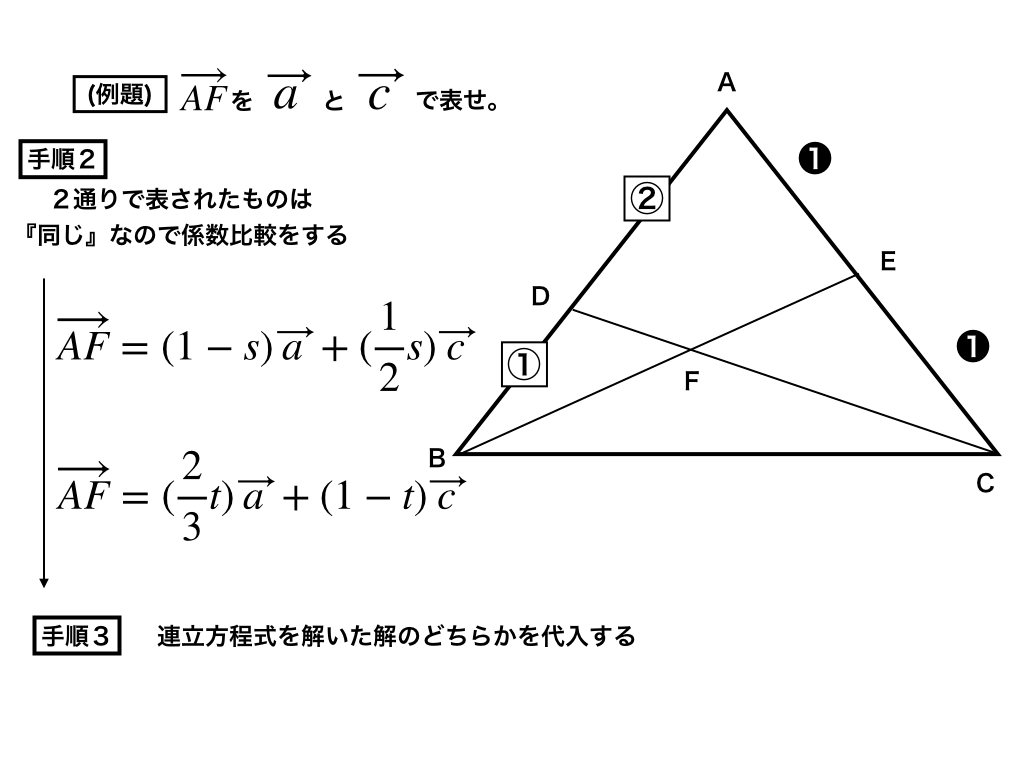
そこで、係数比較をすると、2つの連立方程式ができます。これを解いていくと、sとtが求まります。
手順3
後はsでもtでもどちらでもいいので、求まったs/tをベクトルaとベクトルcの係数に代入します。
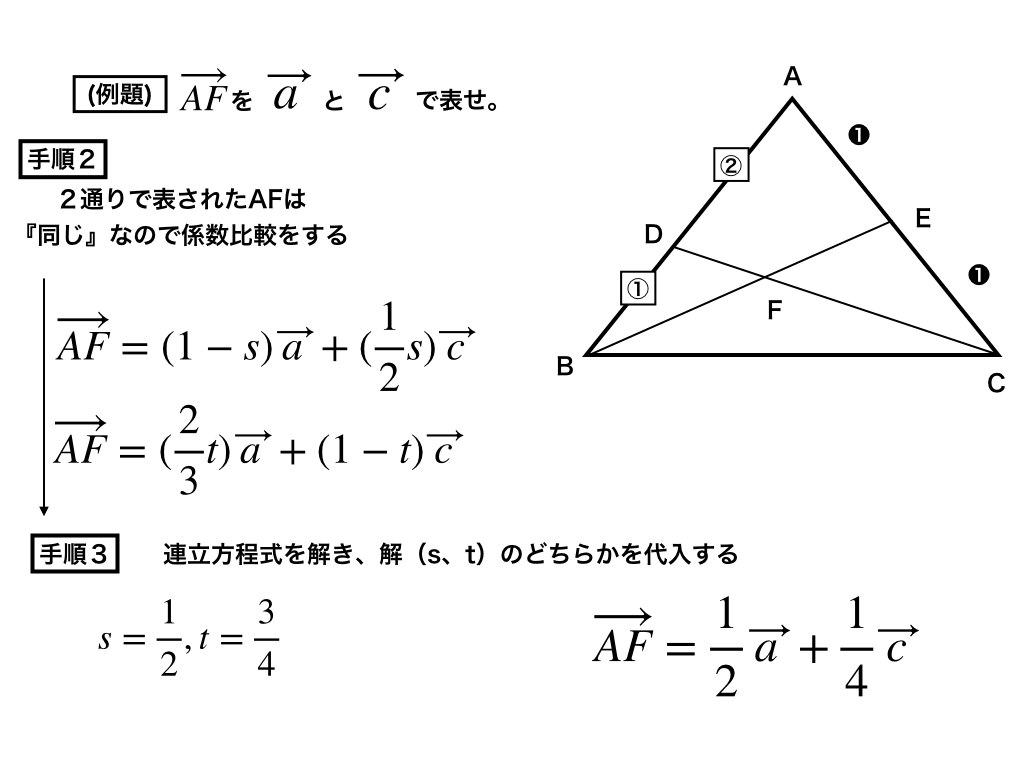
これで、ベクトルAFをベクトルaとベクトルcで表せました。
・・・大分長文になりましたが、理解できましたか?
この種類の問題は本当によく出題される上、高校分野でのベクトルの中で最重要な公式や解法が詰まっているので避けて通れないところなのです。分かりにくいところは何回も読んでみて下さい、
そして理解出来たと思ったらどの教科書や問題集でも類題があるので解いてみて下さい。
分からない所があれば、コメント欄に質問を書いて貰えれば出来る限り解説します。
お役に立ちましたら、シェアしてもらえると嬉しいです!(この文の下にSNSシェアボタンがあります。)
続きは「ベクトルとは?ゼロから始める徹底解説記事9選」を読む。
追記:2018/3/19
一次独立の厳密な定義は以下の引用の様になります。理解できなくても構わないと言う表現について、コメントを頂いたので本連載のスタンスを書いておきたいと思います。
このシリーズではなるべく平易かつ多くの人に理解してもらう為、ある程度感覚的に分かるようにしています。木を見て森を見ずになっては意味が無いと思うからです。ですので、大体高校数学レベルが分かった!となった時、大学以降の線形代数学に入って下さい。
*(このカッコ内の内容は理解できなくて構いません。
ベクトル空間 V の部分集合 S は線型従属でないとき S は線型独立 (一次独立)であるという。明示的には、任意の有限個の相異なるベクトル v1, v2, ..., vn ∈ S とスカラー a1, a2, ..., an に対して
a1v1+a2v2+⋯+anvn=0
ならば (a1, a2, ..., an) = (0, 0, ..., 0) となるとき S は線型独立であるという。言い換えると、集合が線型独立であるとは、集合のベクトルの線型結合によるゼロベクトルの表示が自明なものに限るということである。
引用元:Wikipedia線型独立
カッコ終わり)

