
二次関数のグラフと解の存在範囲
係数の条件決定問題
ここでは、二次関数のグラフを見ながら
・解の存在範囲(どこでx軸と交わっているか)や
・y=ax2+bx+cで表されたの(a,b,c)などの符号(正負)を判定する問題
を解く際に着目すべきポイントをまとめました。
前半は「2次関数の基本」を解説しているので、既に基本部分の理解ができている人は、目次の「二次関数の実践問題」の項からご覧ください。
例題を解きながら、頻出問題の解法を学び定着を目指します。
目次(タップした所へ飛びます)
二次関数のグラフの特徴と注目点
二次関数のグラフ自体はとくに難しい点はなく、以下の<図1>のような形になっています。
ただし、この記事の本題である『解の存在範囲』の問題では、いくつかチェックしなければならないポイントがあり、それを紹介していきます。
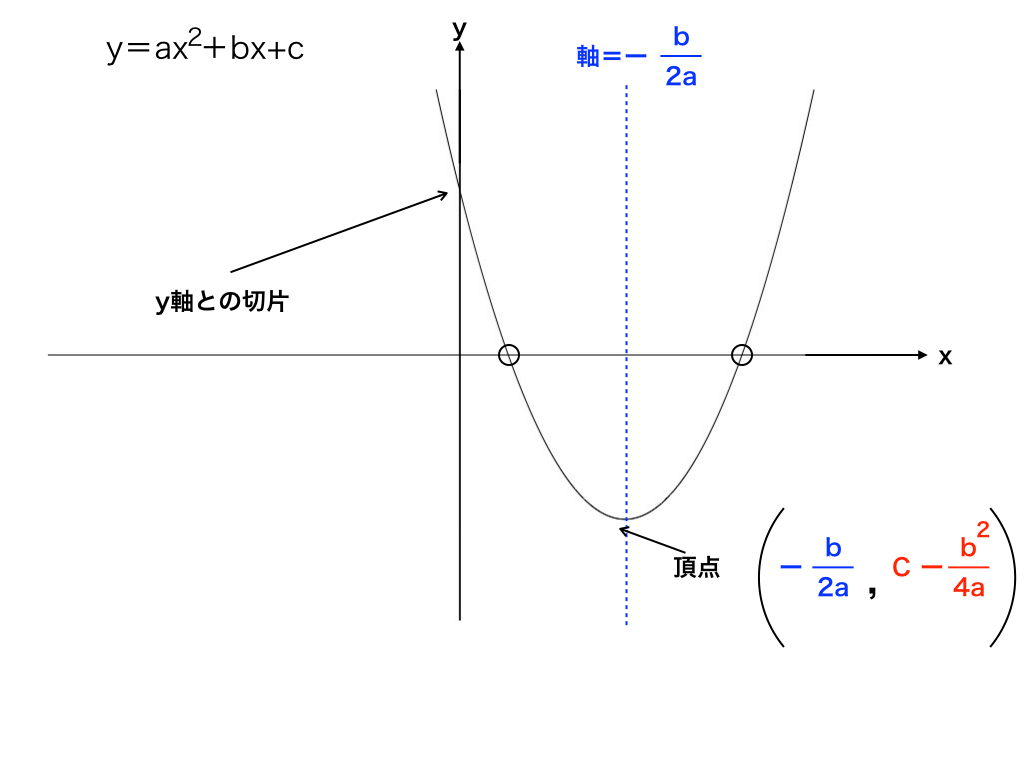
<図1:二次関数のグラフの例>
二次関数の式とグラフ
さて、二次関数の存在範囲や係数決定問題でほぼ必ず確認するのは以下の点です。
(逆に、これ以外に見るポイントはほとんどありません)
・判別式Dとx軸との交点
・グラフが上に凸(うえにとつ)か下に凸か
・軸と頂点の座標
・x=0、つまりy軸や、y軸に並行なx=○での切片の値
一つ一つ、0から解説していきます。
なお、以下の解説ではy=ax2+bx+cの二次関数のグラフを考えます。
判別式とは
判別式D(=b2-4ac)とは、文字通り、二次方程式の解の個数を”判別”するためのものです。
2次関数のグラフでは”解の個数”が”x軸との交点の数”になります。
具体的には、判別式D:b2-4ac>0のとき、実数解が2個;x軸との交点が2個存在し、
D=0のとき、実数解が1個(重解);x軸との交点が1個=x軸と接している状態、
D<0のとき、実数解が0個(解なし);x軸との交点が0個(つまり、グラフが常にx軸より上か下の状態)となります。
判別式Dの値によって解の個数が変わる理由
判別式Dの式を見ると、二次方程式の解の公式$$「\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}」$$の分子にある“ルートの中身”であることがわかります。
\(\sqrt{b^{2}-4ac}{2a}\)の中身が負、つまり\(\sqrt{負}\)であれば、
この2次方程式の解の分子は2乗して負になる数が解となります。
実数にはそのような数が存在しないので、D<0のとき2次方程式の解なし、となるのです。
次にD=0の場合は、解の公式の分子は「-b±√0=ーb」つまり$$「\frac{-b}{2a}」$$の一つの実数解しか持ちません。
よって解が一つ=重解で、グラフではx軸と一点で交わる(接する)と判断できます。
D>0ならば、√の中身が正になるので実数解は2つになります。
上に凸(とつ)下に凸(とつ)とは
上に凸(とつ)下に凸という言葉の意味は、そのままグラフの形を表しています。
上に凸のグラフは、<図2右>下に凸のグラフは<図2左>のようになります。
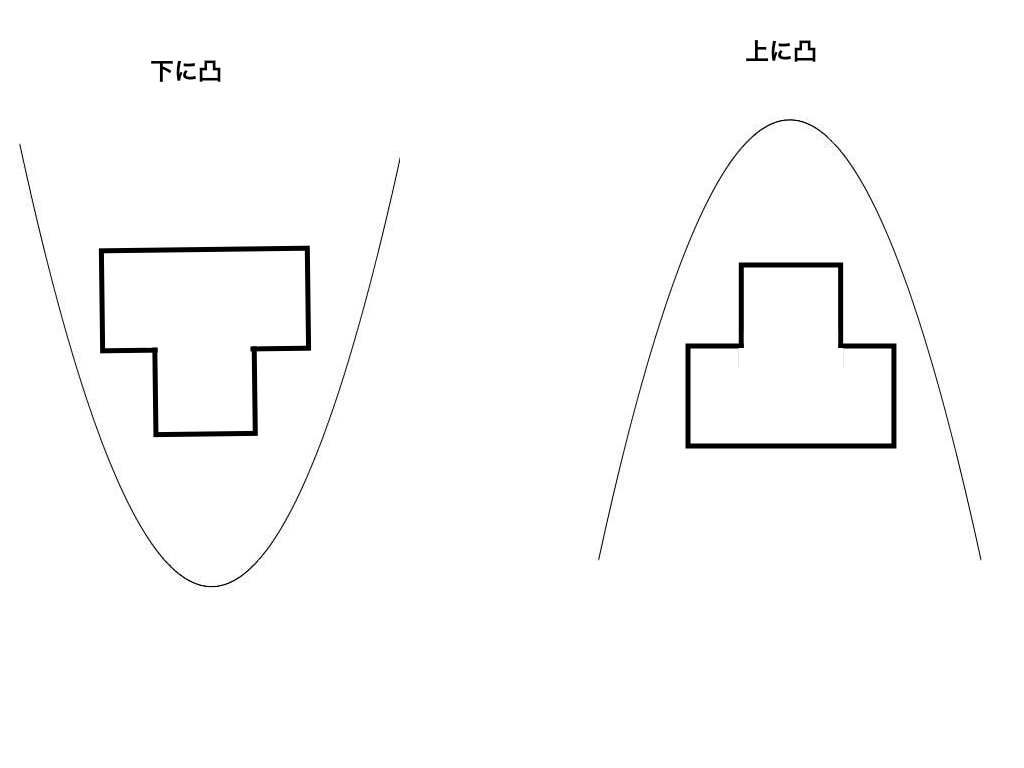
<図2:上に凸と下に凸>
つまり、上に凸=x2の係数が負,下に凸=x2の係数が正の二次関数のグラフであると言えます。
軸と頂点とは
頂点とは、二次関数のグラフにおいて
・“上に凸”のグラフならば“yの値が最大”になるところで、
・“下に凸”のグラフならば“yの値が最小”になるところです。
次に、軸とは頂点のx座標を通りy軸に並行なグラフのことです。

<二次関数の軸と頂点(再)>
\(y=ax^{2}+bx+c\)で考えると、a≠0のとき、平方完成して
$$y=a(x^{2}+\frac{b}{a}x)+c$$
$$=a(x+\frac{b}{2a})^{2}+c-\frac{b^{2}}{4a}$$
より、頂点の座標は(-b/2a,c-b2/4a)、軸はx=-b/2a の式で求めることができます。
y軸での切片とは
y軸はx=0と表すこともできます。
従って、y軸での切片とは、y=ax2+bx +cのxに0を代入した値となります。
二次関数の解についての実践問題
ここまで、二次関数のグラフと、解についての基本的な用語や意味について見てきました。
ここからは、これらの基礎知識を実際にどのように問題に反映させて解いていくのかを紹介します。
グラフを与えられて係数の符号を決める問題
(定数の正負を定める問題)
今、y= ax2+bx+cで表された、二次関数グラフが存在する。(問題図1)
この時以下の(1)〜(6)の正負を答えよ。
(1) a
(2) b
(3) c
(4) a-b+c
(5) a+b+c
(6) b2-4ac
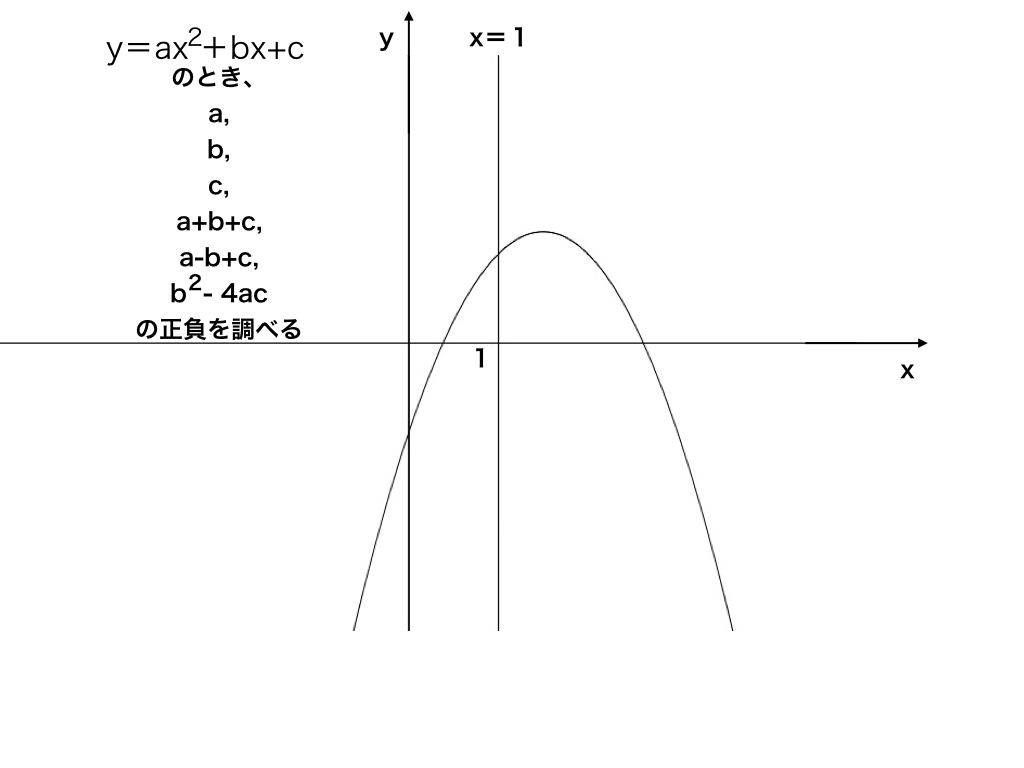
<問題図1>
符号決定問題を解く手順
(1):aの符号は、上に凸か、下に凸かをグラフから読み取ることで簡単に判断できます。
今回は上に凸のグラフなので、x2の前にはマイナスが付きます。よって、aは負。
(2):次にbは、頂点のx座標が $$\frac{-2a}{b}>0$$であることから、
(1)よりaは負、−2aは(負)×(負)より正。
ここで、bが負であるとすると、-2a/bは負になってしまいます。
一方で、bが正ならば-2a/b>0を満たすので、bは正。
(3):この辺りから少し難しく感じる人が出てくるかもしれません。
cの正負を判断するとき、頂点のy座標が正であることを使って考えても良いですが、
(4)(5)で使う、”数値代入”によって問題を解いて見ましょう。
この二次関数のグラフはy=ax2+bx+c の式で表されているので、
x=0を代入すると(右辺)=cとなります。
一方、(左辺)のx=0のときのyの値が知りたいので、
グラフを見るとx=0のとき、y軸の正の部分で交わっています。
したがって、x=0の時yは正→cも正となります。
(4):a+b+c の正負の判断も数値代入とグラフを見比べることで解いていきます。
xが1のとき、y=a+b+cであり、この時のy座標(x=1でのグラフのyの位置)は正になっているので、
a+b+cは正。
(5):この問題は若干難易度が上がります。
【a-b+c】の式にするために代入すべきxの値を考えると、
aはプラスで、bのみマイナスが付いているので、
二乗してプラスとなるx=ー1を代入すれば良いことがわかります。
これまで同様に、x=ー1でのy座標を確認すると0<yなので、a-b+cは負となります。
(6):この式の形は判別式ですね。グラフが異なる2点で交わっているので、D>0 。
よってb2-4acは正と判断できます。
解の配置条件から二次関数の係数の範囲を求める問題
二次関数y=x2+kx+2のグラフが、次の(1)、
y=x2+2(k-1)x+3ーk2のグラフが、(2)
の条件を満たすためのkの範囲を求めよ。
(1)x軸の正の部分と異なる2点で交わる
まずは、x軸とy=x2+kx+2のグラフの交点が、<図2>のようになる場合です。
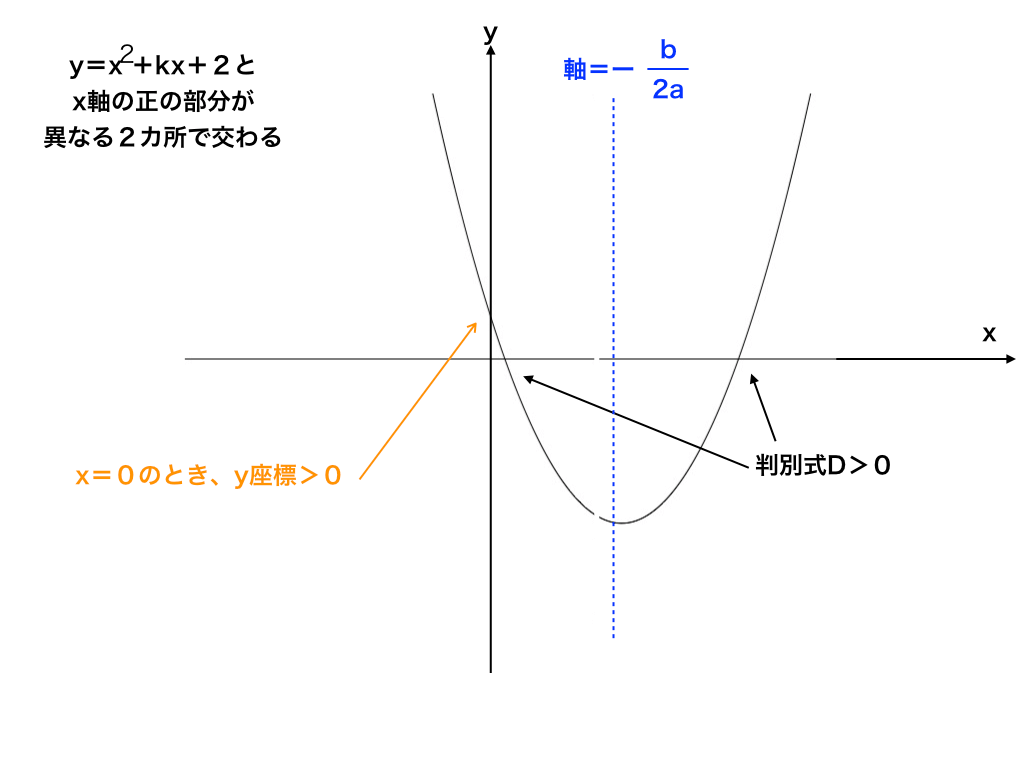
<図2-(1)>
以下に条件式を挙げていきます。
まず異なる2点で交わるので、判別式D>0。
次にx=0のときy切片>0。
→(この条件がないと、x軸と交わる点が『正に1つ、負に1つの場合も含んでしまう』ので、注意が必要です。)
三番目の条件は、軸(→x=-b/2a)が0より大きいことです。
→(条件1、2のみだと、『x軸の負の部分で2交点を持っている』場合を除けない)
※条件2,3の()に書いた通り、このタイプの問題では条件式を立てる際に“モレがないか”慎重に確認しながら解いていくことが大切です。
条件1〜3より、
\(k^{2}-8>0\)
\(-\frac{k}{2} >0\)
y=2
を満たすkの範囲は\(k<-2\sqrt{2}\)・・・(答)
(2)x>0とx<0の異なる2点で交わる
今度はx軸の正の部分と負の部分で、一つずつ交点を持つ場合を考えます。
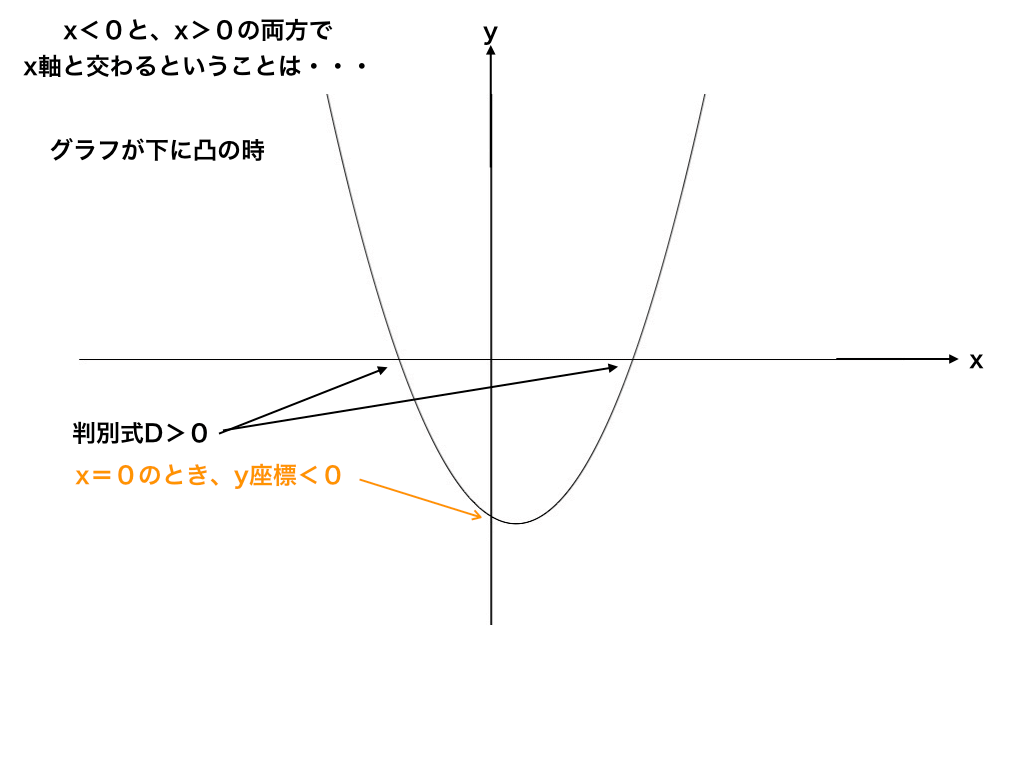
x軸の正と負の部分にそれぞれ一つ交点を持つ条件を考えると、まず判別式D>0であることは必須です。
そして、これだけでは“どこでx軸と交わっても良い”ことになってしまうので、x=0のとき、y<0であれば、問題の条件を満たします。
(仮にx=0、y>0であれば、正で異なる2解を持っても、負で異なる2解を持っても良いことになってしまいます)。
したがって、条件はD>0かつf(0)<0より、
\(判別式D=4(k-1)^{2}-12+4k^{2}>0\)
k<ー1
\(条件2::3-k^{2}<0\)
√3<k、ー√3>k
を合わせて、k<-√3・・・(答)
二次関数のグラフと応用問題まとめ&関連記事
・今回は2次関数のグラフの基本〜解の配置・係数の範囲の問題を扱いました。
・この分野は数学1だけでなく、数学2「図形と方程式」など、今後いろいろな単元で必要となる非常に重要なものなので、基本を今のうちに習得しておきましょう。
<現在二次関数の関連記事を作成中です。・・・>
二次関数のグラフの最大・最小値を求める応用問題についての記事を作成しました。
「二次関数の最大値・最小値の求め方(グラフや定義域が動くパターン)」
2次方程式・二次関数との融合問題が頻出の、”絶対値”についての解説記事を作成しました。

