電流が作る磁界(=磁場)3タイプと”右手(右ねじ)の法則”
<この記事の内容>:電流が作り出す磁場”3”パターンの公式と、向きの調べ方についてイラストを豊富に使用しながらそれぞれ紹介しています。
<電気分野の復習>:「高校物理/物理基礎の電磁気分野の記事を総まとめ!」これまでの”電磁気”について左の記事にまとめています。予習・復習にご利用ください。
目次(タップした所へ飛びます)
電流が作り出す磁界まとめ
ここからは電流が流れることによってその周りに磁場(磁界)ができる、3つのパターンと効率的な覚え方を見ていきます。
右ねじ(右手の法則)
これから解説する以下の3パターンはそれぞれ似ているためによく間違えやすいです。
そこで、磁場の向きを”たった一つの方法”で見分けることができる方法を紹介していきます。
なお、いわゆる『右ねじの法則』と同じことをしているのですが、より分かりやすい右手を使った方法で進めます。
直線の電流が作る磁界
まずは最も基本的なパターンである、『直線の電流が作る磁場』です。
磁場の向きをチェック(1)
磁場の向きを『右手の法則』を使って調べてみます。
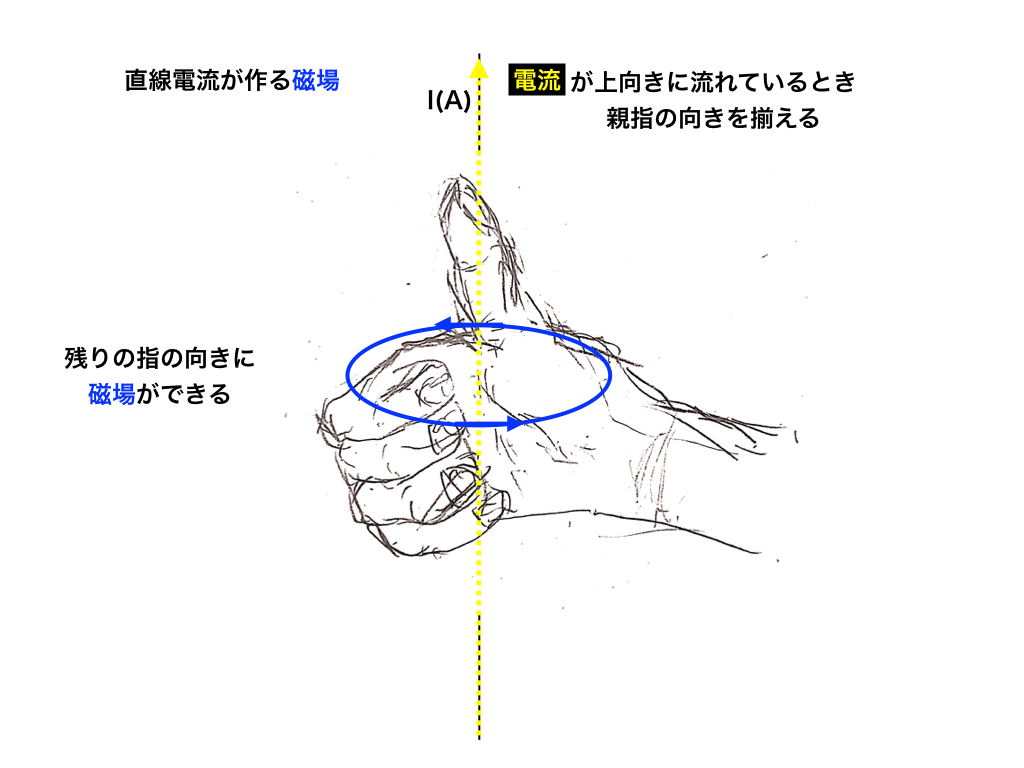
この図のように、電流が流れる方向に親指の向きを揃え、残りの小指〜人差し指をクルッと手のひらの方へ回転させます。
この時の小指〜人差し指の先の向きに磁場が発生します。
磁場の強さの式
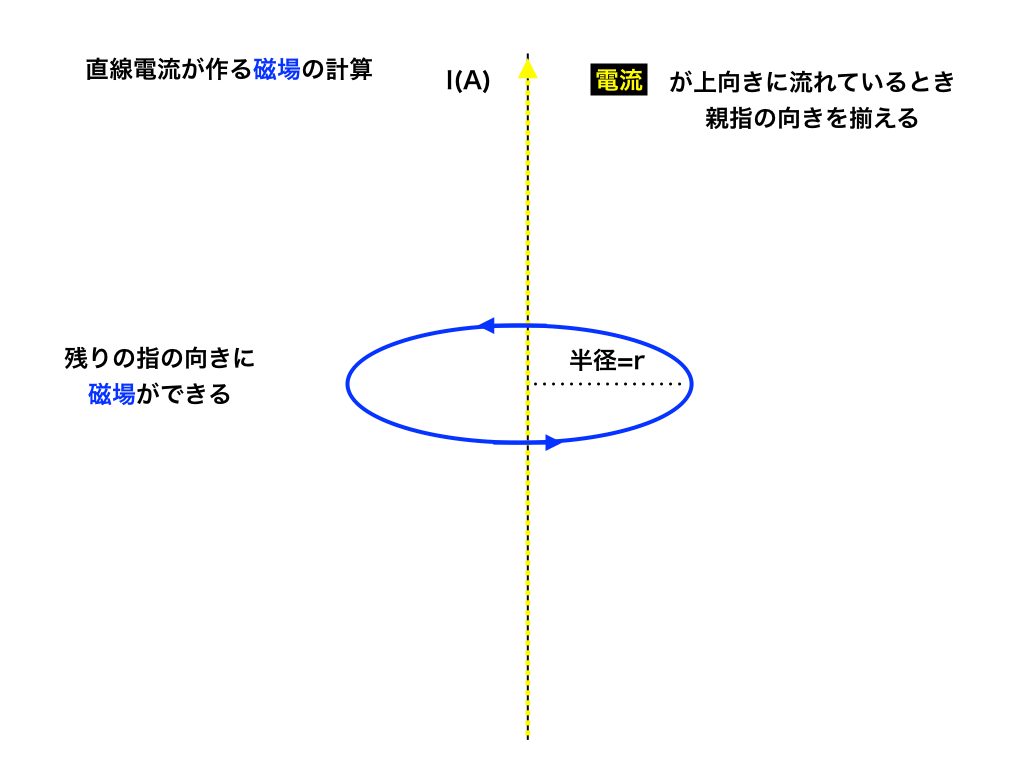
上の右手を使った方法で磁場の向き(回転する方向)がわかれば、次はその強さ(単位:A/m)を求めてみましょう。
$$H=\frac{I}{2\pi r}$$
上の式が電線からr(m)離れた位置での磁場の強さです。
中心にある電流が流れる導線から遠ざかるにつれて、
”rが大きくなる→Hの分母が大きくなる→Hは小さくなる”ことが分かります。
円形の電流による磁界の向きと大きさ
今度は電流が円のように回転する場合(1回巻きのコイルをイメージしてみてください)です。
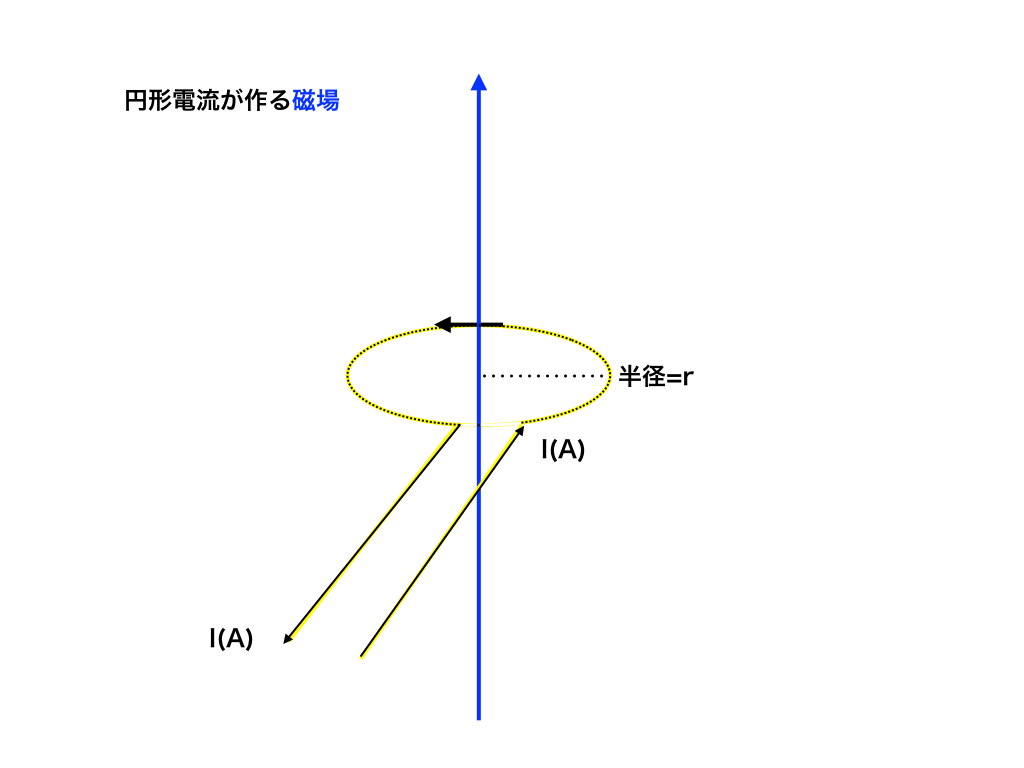
磁界の向きをチェック(2)
円形でも先ほどと同じく右手を使って磁場Hの向きを調べます。
電流が流れる向きに小指〜人差し指を揃えて、親指が向く(以下の場合は上向き)方向に磁場が発生します。
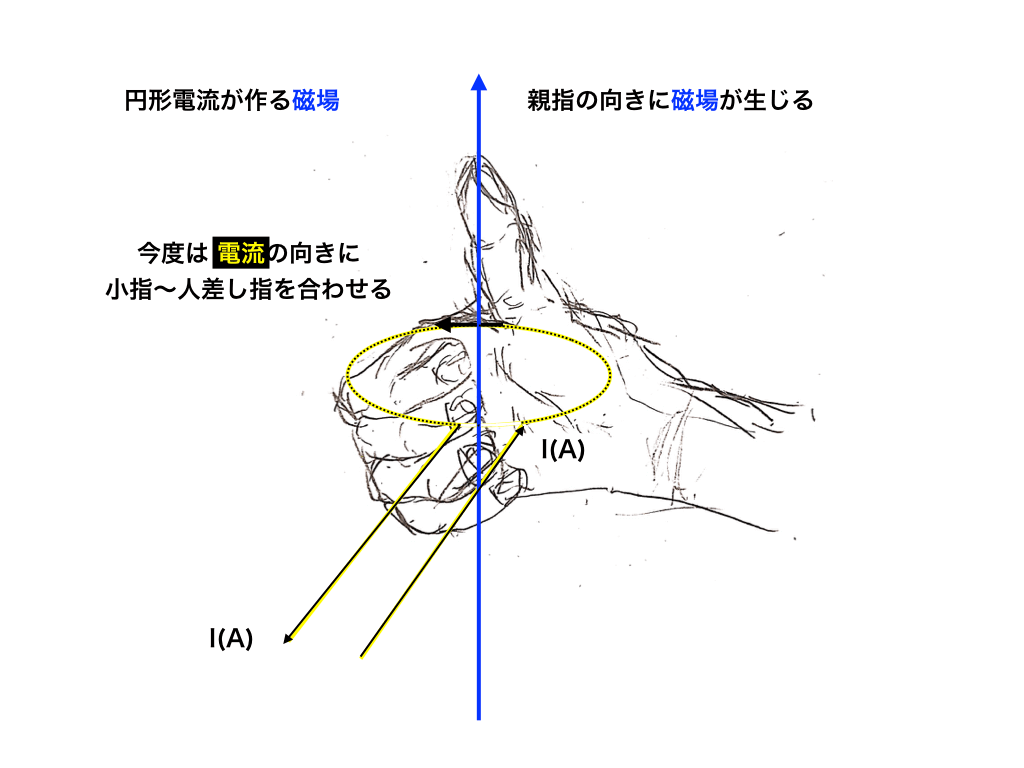
直線電流の時は”電流が親指”、”小指〜人差し指が磁場”であったのに対して、円形の場合にはイラストのように”電流の向きが小指〜人差し指”、”親指の向きが磁場の向き”となって、電流と磁場の関係が真逆になっていることに注意しましょう。
磁場の強さの公式
円形の電流の中心部を通る電場Hは$$\frac{I}{2r}$$で求まります。
(ここでは、先ほどの直線の場合と異なって、”円周率π”がありません。)
<図4>
n回導線を巻いた場合
上の場合は”一回だけ電流が円形に流れる”場合を考えました。
これ今度はコイルのように何度も巻いて2、3、・・・とn回導線を巻いてみると磁場Hの大きさ(A/m)はどう変化するでしょうか?
結論から言うと○回巻いた分だけ、○倍磁場は強くなります。
式で表すと$$H=n\times \frac{I}{2r}=\frac{nI}{2r}$$
となります。
単純ですが次項で解説する”ソレノイド(コイル)との違い”でよくミスをしやすいので、しっかり違いを確認していきましょう。
ソレノイドの意味と磁界
さて、主な3つの電流が作る磁場の最後です。”ソレノイドコイル”と呼ばれるものを扱います。
今述べたように上の項で解説した、円形の電線を何度も巻いたものによく似ています。
が、少しだけ注意が必要なので、その点について紹介しておきます。
磁界の向きをチェック(3)
円形の電流の時と同じように”電流の向き”と”小指〜人差し指の向き”を揃えると、親指が向く方向と磁界の向きが一致します。
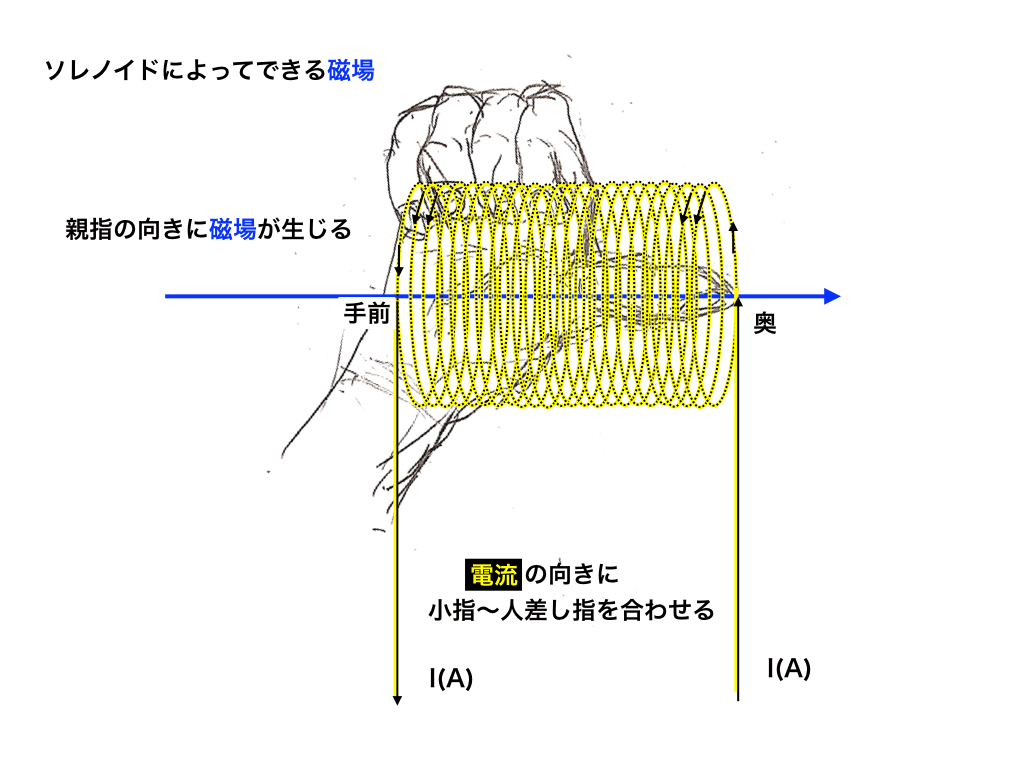
(上の図について:右の導線が奥にあり、左の導線が手前にあります)
磁界の強さの公式
さて、最大のポイントである”円形の電流とソレノイド(コイル)”の作る磁界の公式に入ります。
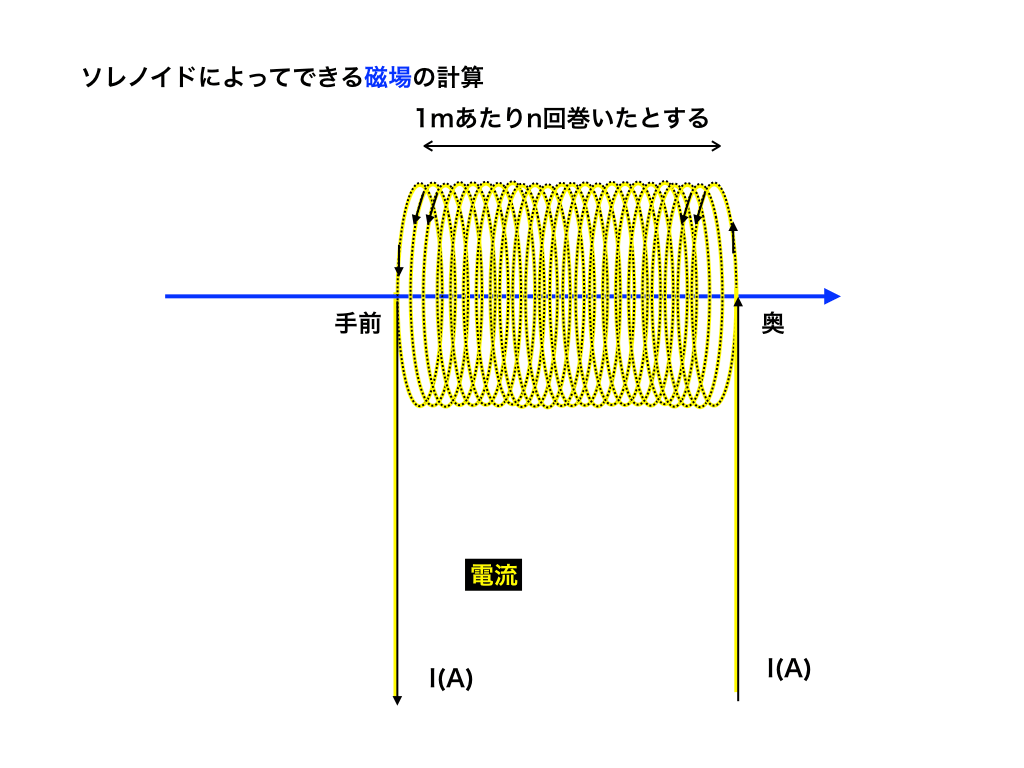
※nは単に巻いた数ではなく、”1m辺りに何回巻いてあるか”を意味します。
従って、n回巻きの円形電流の式と混同しないように注意が必要です。
\(\mathrm{H=nI}(ただし,n(回巻/m^{2}),I(A)\)
少しややこしいので、2つの違いを簡単な例題で確認しておきましょう。
ソレノイドと円形電流の作る磁界:確認例題
(例題1):いま<図4>のような円形の導線を100回巻いたものに、2(A)の電流を流した。
半径を0.5(m)とする時、中心部分にできる電場の値を求めよ。
(例題2):長さが0.5(m)で100回巻いてあるソレノイドコイルに2(A)の電流を流した。
この時中心部分にできる電場の強さを求めよ。
例題の解答と解説
どちらも100回巻いていることには変わりありません。
が、ソレノイド(コイル)の公式”H=nI”の”n”は、”1m辺り何回”巻いたか、だったのでこの問題ではn=100÷0.5=200となります。
従って、例題2の解答:\(H=200\times 2=4.0\times 10^{2}(A/m)\)
一方、円形電流の方は公式をそのまま用いて、$$例題1の解答:H=\frac{100\times 2}{2\times 0.5}=2.0\times 10^{2}(A/m)$$
電流が作る磁場1~3まとめ
・3種類の電流が作る磁場(=磁界)の向きは右手を使う事で全て解決できるので、出来るだけ早くに身につけましょう。
・円形の電流とソレノイドの相違点を復習
・次回は『フレミングの法則と電磁力』について扱います。
電磁気まとめページと続編「ローレンツ力」へ
これまでの電気・磁気分野は、>>「高校物理:電磁気の解説記事総まとめ」<<でご覧いただけます。
磁気分野第一回:「今ココです」
磁気分野第二回:「フレミングの法則と電磁力・ローレンツ力」
磁気分野第三回:「ローレンツ力によって運動する荷電粒子の問題1」

