
斜め方向のドップラー効果と上空の飛行機の問題
「救急車が近づくと音が高くなり、遠ざかると音が低くなる」という現象に代表されるドップラー効果。
音源や観測者が動くことによって、観測者に聞こえる音の振動数が大きくなったり、小さくなったりする現象のことです。
この記事はそのドップラー効果の第3回目です。先にドップラー効果の基礎・公式の導き方を学びたい人は以下のリンクよりご覧ください。
第一回:「ドップラー効果の公式の導出と覚え方【理解して覚えよう】」(必須)
第二回:「反射板や風が吹いている時のドップラー効果」(今回は使用しません)
さて、今回は“斜め方向のドップラー効果”と“上空を飛ぶ飛行機の音のドップラー効果”の問題を解いていきます。
まず<斜め方向のドップラー効果>で解法をマスターし、<上空を飛ぶ飛行機の音のドップラー効果>で更に演習してみましょう。
目次(タップした所へ飛びます)
斜め方向のドップラー効果
今回は、例題を解きながら斜めドップラー効果について解説していきます。
斜めドップラーの問題
以下の条件で、Aが観測する振動数F(Hz)はいくらか。
ただし音速はV(m/s)、音源は固定されており、その振動数をf(Hz)、Aがy軸の正の方向に速さ\(v_{o}(m/s)\)で移動する。
また、図1のようにAからy軸に対して角度θ方向から音が聞こえるものとする。
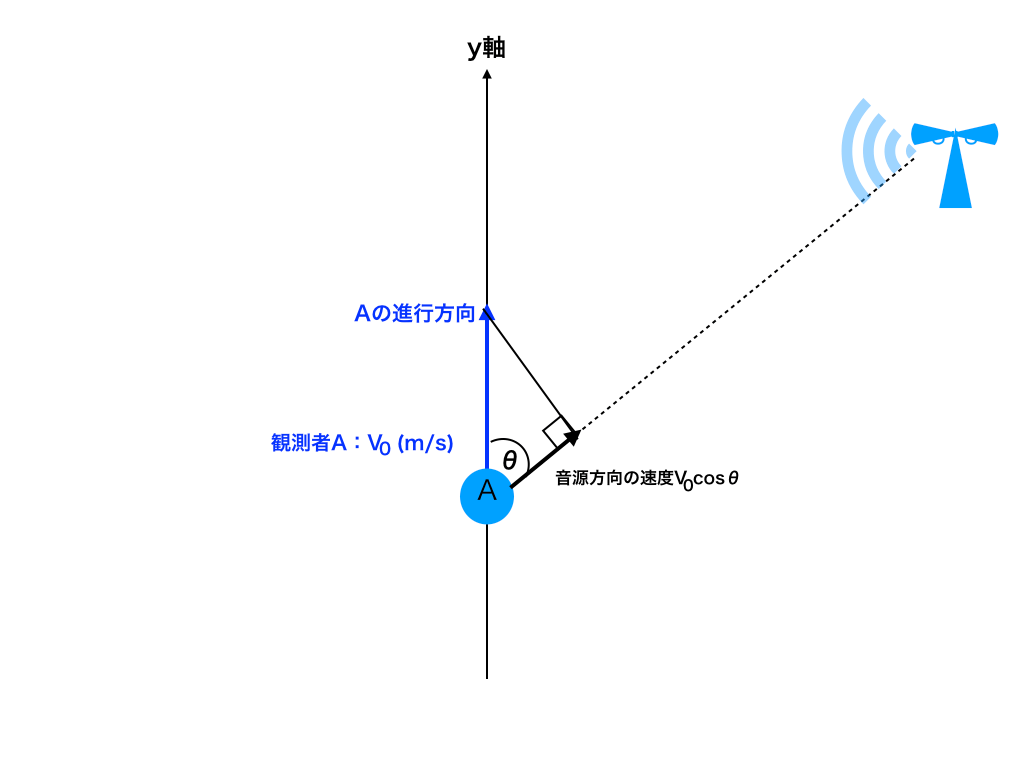
<図1>
ⅰドップラー効果の公式を確認する
簡単にドップラー効果の基本式を復習しておきます。
$$F=f\times \frac {\left( V\pm v_{o}\right) }{\left( V\pm v\right) }$$
F(Hz):観測者の聞く周波数、
V(m/s):音速、
\(v_{o}(m/s)\):観測者の速度、v(m/s):音源の速度、
f(Hz):音源から発せられる周波数
音源とAが直線上にある成分のみ計算する
今回の様な"音源と観測者が斜めに位置するドップラー効果"を解くときのポイントは、音源/観測者に一直線で届く成分に分解する事です。
音速がV(m/s),かつ音源の速度v=0(m/s):固定より
・観測者条件:等速直線運動、速度\(v_{o}\)
・音源条件:観測者に対して角度θ方向に位置
力や速度を成分に分解したり、合成するときなどに使用するのが三角比(三角関数)でした。
以前の解説記事→(参考:「物理/物理基礎の為の三角比とベクトル」)
ここでも“三角比”を用いて問題を解いていきます。
Aの移動速度\(v_{o}\)を分解すると、音源方向への成分は\(v_{o}\cosθ\)となり、
この速さで音源に真っ直ぐに向かって走っていることと同じになります。
音源へ向かっていく→受け取る波の数が増える
→Fが大きくなる
→これをドップラー効果の式
$$F=f\times \frac {\left( V\pm v_{o}\right) }{\left( V\pm v\right) }に当てはめると$$
$$F=\frac{f(V+v_{o}cosθ)}{V}$$
試しにこの式のθに30°を代入すると
$$F=\frac{f(V+v_{o}cos30°)}{V}$$
$$⇔F=f\left( \frac {V+\frac {v_{0}}{2}}{V}\right) $$
分母が大→周波数大→高い音が聞こえる、となります。
更に、θ=150°つまり音源からどんどん離れていくときを考えると、
$$F=\frac{f(V+v_{o}cos150°)}{V}$$
$$⇔F=f\left( \frac {V-\frac {\sqrt {3}v_{0}}{2}}{V}\right)$$
分子が小→周波数が小→低い音が聞こえる、こちらも感覚と一致します。
この問題では、音源が斜め方向から聞こえてくるために“音源の方向に観測者の速度を分解”しました。
ただ、難しい問題になると、音源も速度を持っていたり、進行方向が逆であったりします。
しかし、しっかりと図を作成し成分を適切に分解していけば必ず解くことができます。
次は試験で出題されるような問題で、一度解いてから解法を見ていきましょう。
上空を飛ぶ飛行機の音のドップラー効果
(問)<図2>の様に観測者は動かず、飛行機が一定の高度で一直線上を西から東へ等速度v(m/s)で飛んでいる。
音速をV(m/s)、飛行機の出す音波の振動数をf (Hz)また、V>vとして、以下の問いに答えよ
問1:十分遠方の西側(θ=0)から聞こえる振動数Xを求めよ
問2:十分遠方の東側(θ=180)から聞こえる振動数Yを求めよ
問3:飛行機が真上に見えた時の振動数Zを求めよ
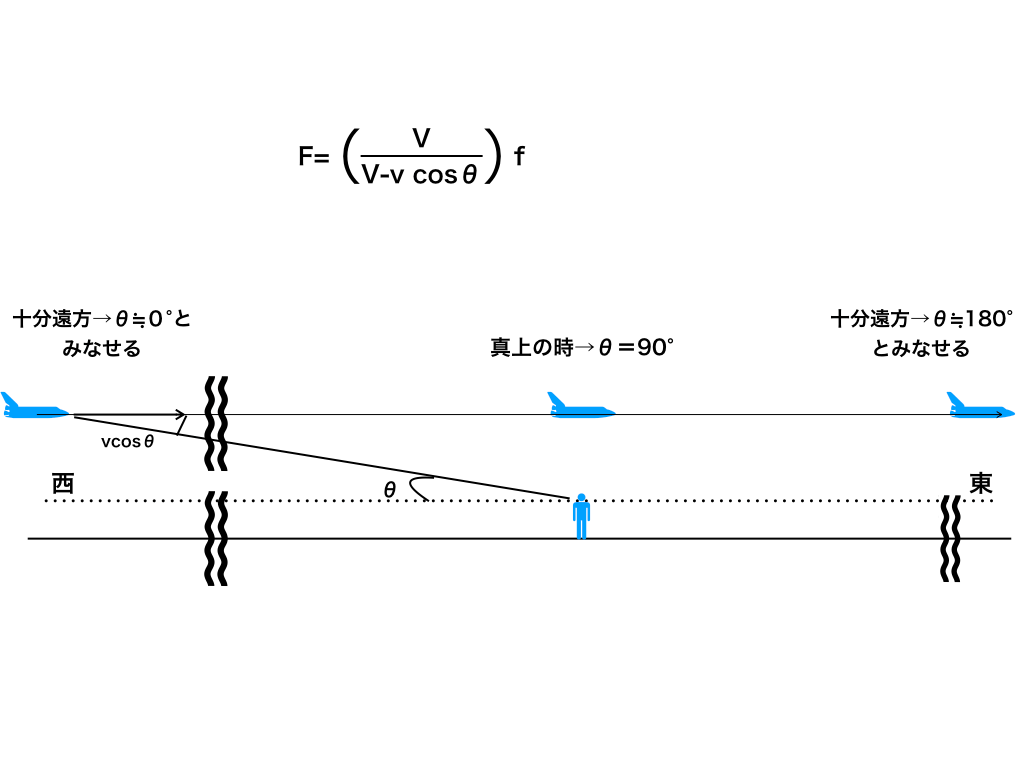
<図2>
まずはドップラー効果の公式を思い出して、
$$f'=f\times \frac {\left( V\pm v_{o}\right) }{\left( V\pm v\right) }$$
図を描き、観測者の条件と音源の条件で計算し揃えなければならない部分を確認します。
$$音速=V、音源の速度=v 、観測者は固定v_{o}=0$$
→よって、音源の速度を観測者の方向に分解すれば良いので、
成分はvcosθ。ドップラー効果の式の分母に代入して
$$F=\frac{fV}{V-vcosθ}・・・(*)$$
<問題1>十分遠方の西側(θ=0)から聞こえる振動数を求めよ
観測者に対して十分遠方ということは、<図2>の様に高さを無視しても良い=θ≒0であるので、Bの西側左手方向に飛行機がいる。
よって音源がθ=0方向から聞こえてくるため、飛行機の移動方向を観測者に揃える。
音源が近づいてきて、観測者は動かないのでこれは周波数が大になるパターンです。
(*)式に0°を代入して、
$$F=\frac{fV}{V-vcos0°}$$
$$cos0°=1より、答え:F=\frac{fV}{V-v}$$
<問題2>十分遠方の東側(θ=180)から聞こえる振動数を求めよ
観測者に対して十分遠方の東側、つまり、右手方向に飛行機がいるため、観測者と飛行機の角度θは180°になる。
よって音がθ=180°方向から聞こえてくるため、(*)式に180°を代入して、
$$F=\frac{fV}{V-vcos180°}$$
$$cos180°=-1より、答え:\frac{fV}{V+v}$$
<問題3>飛行機が真上に見えた時の振動数を求めよ
観測者の真上なので、観測者と飛行機の角度θは90°になる。
角度が90度の時は、普段みなさんがスピーカーの前で音楽を聞くように、ドップラー効果は発生しません。
よって、音源の発した周波数と同じ周波数を観測者が認識することになります。
従って答えF=f となります。
ちなみに(*)式のθに90°を代入するとcos90°=0より
$$F=\frac{fV}{V-vcos90°}$$
$$⇔F=\frac{fV}{V}=f$$
まとめとドップラー効果の関連記事(必読)
ドップラー効果の問題を解くときのポイントは
『観測者と音源を一直線上の成分に分解して公式にのせること』です。
斜め方向であっても、基本となるドップラー効果の式が理解できていれば対処できます。
入試などで応用問題が出ても冷静に解くことが出来るように、普段の勉強や模試でインプットとアウトプットを繰り返して、体に染み込ませましょう。
もう一度ドップラー効果の式の基本を確認する>>「ドップラー効果とは?その意味と公式の導出」<<
今回は扱っていませんが、頻出の”風”や”反射板”が関わる問題>>「(応用)風が吹いていたり、反射板がある時のドップラー効果の考え方」<<
次回は、「うなり」と言う現象の解説と、風が吹いている状況で反射板/音源/観測者が動く様な更に複雑な場合など“ドップラー効果の総仕上げ”を行います。

