
交点の位置ベクトルを解く
目次(タップした所へ飛びます)
ベクトル方程式は苦手意識を持つ人が多いです。
この記事を読んでいるあなたもそうではないでしょうか?
今回はベクトル分野で頻出の交点に関する例題を通して、ベクトル方程式に慣れてもらえればと思います。
ベクトル方程式(直線)とは、「点aを通り傾きがdの時、u=a+tdで表される式」です。が、この説明がイマイチ良く分からない。もう少し詳しく説明すると、今適当な点Oから点aに向かい、dの傾きに沿って連なる点の集合です。
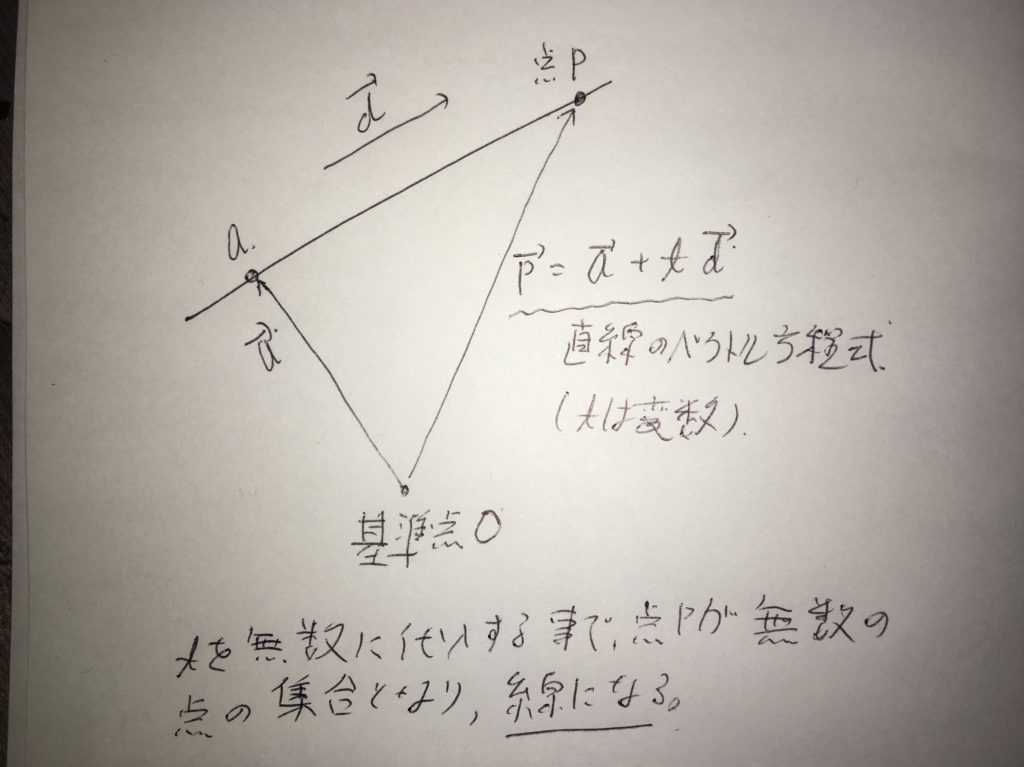
”わざわざある点aを経由して目標の点(傾きがdの線上)に向かう”というイメージです。
この「わざわざある点を通る」事により、応用が効く様になる上、計算量も減ります。
これだけでは??だと思うので、具体的に解説していきます。
例題で学ぶ
三角形ABCと点E、点Fがある。
但し、点Eは辺CAを5:1に内分、点Fは辺ABを1:3に内分した点である。BEとCFの交点をPとする。
(1)この時、ベクトルAPをベクトルABとベクトルACで表せ。
(2)この時、ベクトルAPと辺BCの交点をDとする。AP:PDの比を表せ。
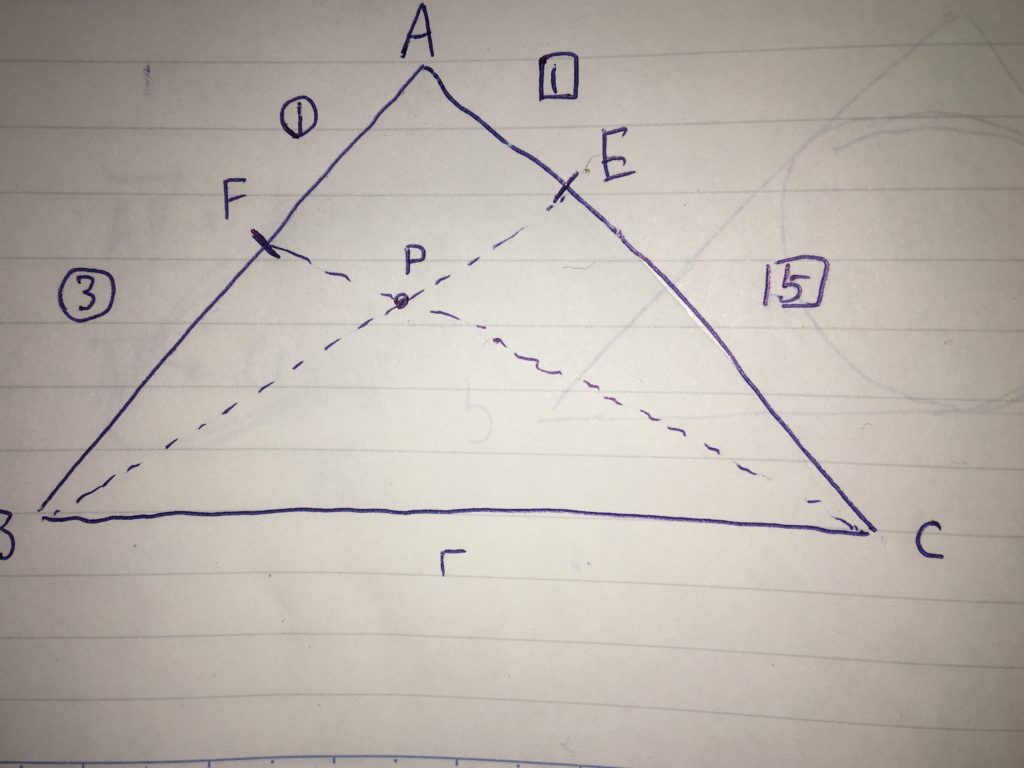
この類の問題は、一度は目にしたことがあると思います。多くの場合、「sとtの二文字を用いて、点Pを通る辺を s:(1-s) と t:(1-t) に分けて、
ベクトルの内分点の公式を使い、sとtを求めて解く」という流れが一般的です。
しかし、この解法だと(2)では少し時間がかかり余りおススメ出来ません。
今回はこれをベクトル方程式で解いていきます。
途中で?な所が出てきても、読み進めていって下さい。何度かこのページを読んでいる内に段々と慣れて来ます。
(1)さて、ベクトルAPをベクトルABとACで表せとあるので、AP=x AB+y AC•••@といきなり設定してしまいましょう。xとyがわかればそれで答えが出ます。
ベクトル方程式は“わざわざある点を経由”でしたね。ここでわざわざ点Eを経由してみます。
問題文より、6AE= ACなので、@に代入すると、AP=x AB+6yAE … #1と表せます。
同じく、わざわざ点Fを経由します。
4AF= ABより、@に代入して
AP=4xAF+yAC …#2 と表せます。
ここで「係数和1の法則」という法則を知っておく必要があります。
#2018/04/07追記
係数和1の法則が使える条件と理由←このリンク先記事で「係数和1の法則」を解説しているので、曖昧な人は必ず読んで理解しておいて下さい。
これは、#1を例にすると、辺BE上に点Pが有れば、その係数 はx+6y=1となる 法則です。
これを用いて、
#1より x+6y=1
#2より 4x+y=1
この連立方程式を解くと、
x=5/23、y=3/23 となります。
よってAP=5/23AB+3/23AC (1了)
(2)問題文より、AD=k AP と表せる。
これにAP=5/23AB+3/23ACを代入して
AD=k・5/23AB+k・3/23AC #3
DはBC上の点でしたよね?ここでも「係数和1」が使えます。
つまり、5k/23+3k/23=1
よって、8k/23=1、 k=23/8となります。
AD=k AP から、AからPまでの距離を8とすると、ADの距離は23になるという事です。
従って、APDは一直線上にあるから、
AP:PD=8:15 (2了)
少し大変だったと思います。是非繰り返し読んで、類題を実際に解いてみて下さい。
特に(1)ではベクトル方程式を使わない解答が多いかも知れません。
しかし何通りかのアプローチの仕方を持っていると、思わぬ効果が得られる事があるので是非「ベクトルを0から解説!記事総まとめページ」←の記事で身につけてもらえたらと思います。
お疲れ様でしたm(._.)m

