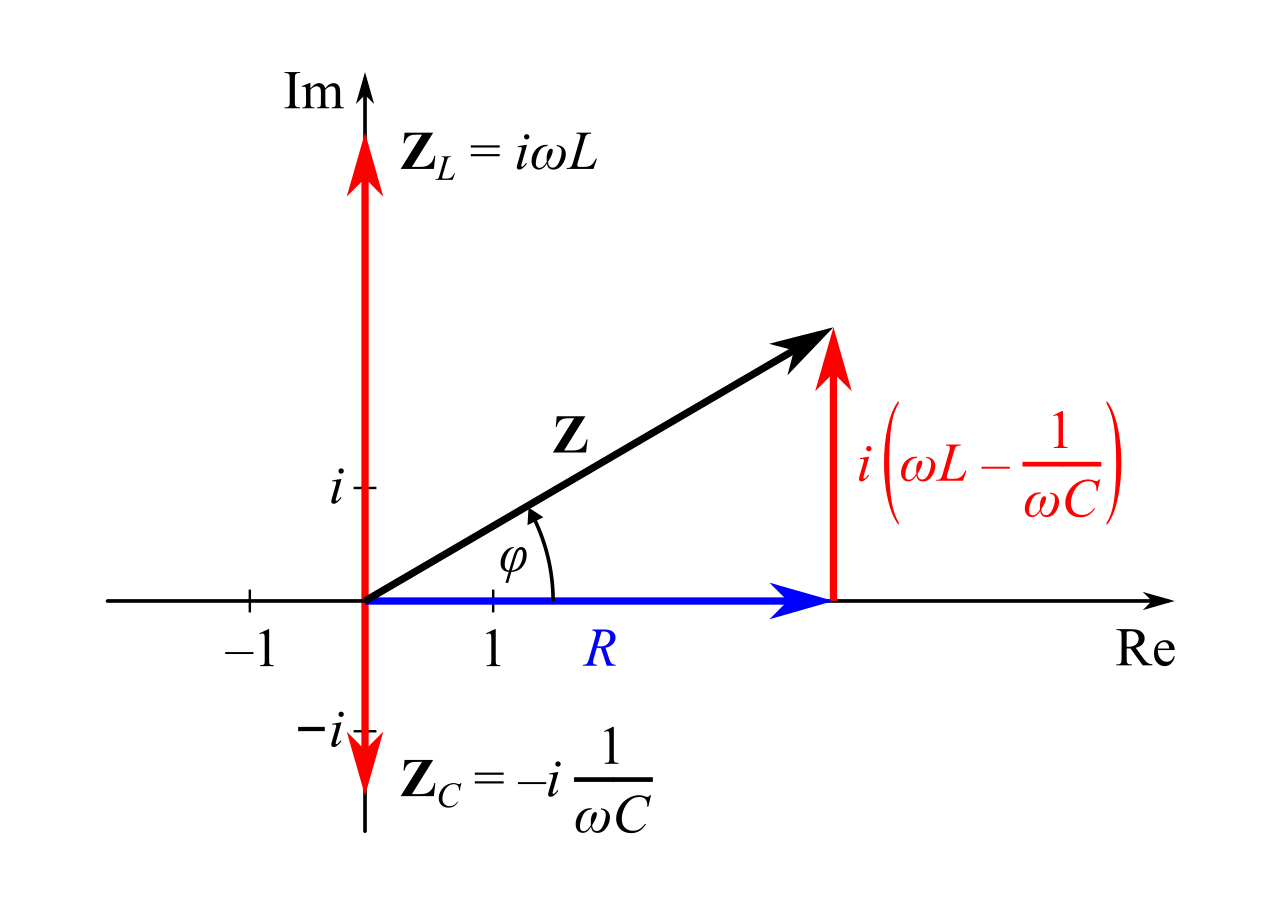
image by Zátonyi Sándor
今回は高校物理の中でも最も複雑(と思われている)分野ー交流ーを扱います。
※:この記事は現在内容の更新等を逐次進めています。それまでは>>「交流回路とRLC直列回路」、「電気振動とLC回路」を参照ください。
交流自体は特別複雑な考えではなく、一般に三角関数が解っていれば電流の大きさと向きがsinグラフの様に変化していくだけです。
※正弦波の他にも三角波やノコギリ波等々ありますが高校範囲外です
直流は電流の向きと大きさが同じでした。
しかし!交流回路を直流回路と同じ様に解こうとした途端、
悪夢のような数式やインピーダンス、リアクタンス、位相・・・の様
によく分からないコトバだらけになり結果苦手意識を持ったまま受験へ突入、
という人が毎年沢山居るのです。
さてこの記事の読者は2通りに分かれる筈です。すなわち、
type1学校等で一通り交流を勉強した人
type2まだ交流は未習だが興味があって見に来てくれた人
type1の方は既に一般的に正式とされている方法ー三角関数や微分を使って数式と格闘して解くーを経験していると思うので、驚く程あっけなく解けるこの記事をそのまま読み進めてください!
type2の方はやはり一度は上記の正式な方法を経験しておく必要があると思います。その方法は教科書や参考書ならばどこでも載っているので、この記事を読んでからでも良いので目を通しておいて下さい。
但し、type2の方はこの記事を見ながら教科書を手元に置いて同時に進める事を強くオススメします。よく分からない単語等がすぐ調べられますし、解法を比べていかにベクトル法が楽か分かってもらえるからです。
※ベクトル法は筆者が付けた名前なので、試験などでは書かないでください!(この方法の下敷きには複素平面が深く関わっていますが、最難関大入試レベルでも必要ない高度なお話なのでぜひ是非大学で勉強して下さい。)
さあ、type2の方も準備できましたか?type1の方お待たせしました。ココから本題に入ります。
今回は交流回路の中でも一つの大きなテーマかつ交流のエッセンスが凝縮されているRLC直列回路を通してベクトル法を解説していきます。
RLC直列回路とは図1の様な回路です。
(R:抵抗/L:コイル/C:コンデンサー)
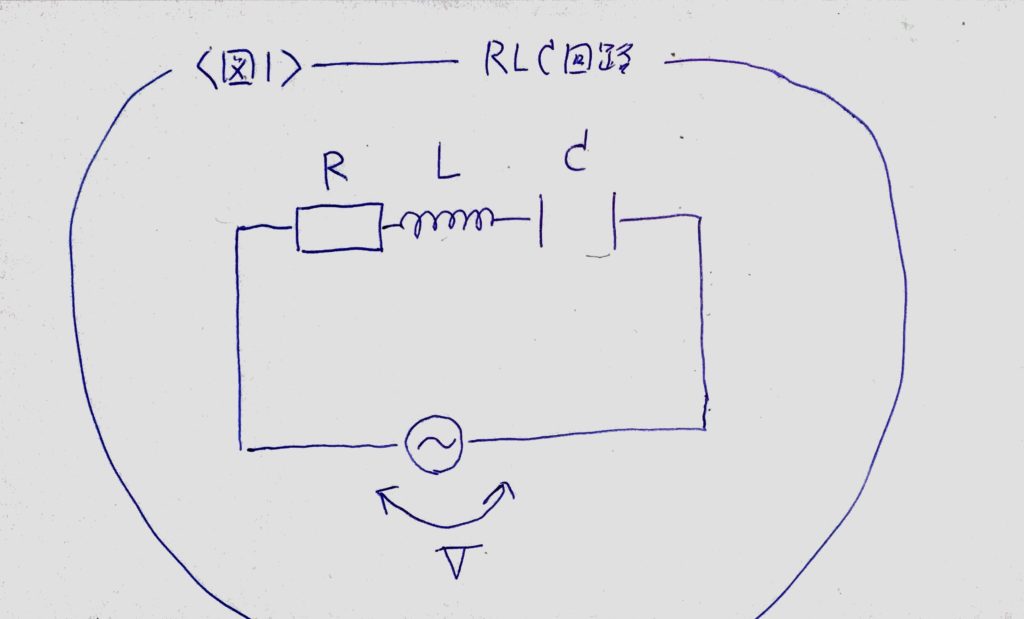
図1
直列回路と違ってオームの法則V= IRが使えません。それで苦労するのですが、考え方自体はマネ出来ます。
直列回路なのでRLCそれぞれにかかる電流Iは同じです。よって、I=I0sinωtと置きます。
オームの法則をマネします。V= IRを考えるとRが解っていません。
そこで最低限覚えて欲しい事として、直流における抵抗は、交流回路に於いてはリアクタンスと呼ばれ、R(抵抗)だけでなくL(コイル)とC(コンデンサー)にも抵抗と同じように電流を妨害するものとして存在するという事です。
そして、普通の抵抗と違って電流と電圧が同時にかかる(同位相)<タイミングの事>訳ではなく、時間のズレが生じるという事です。
その抵抗値とVーiのズレを図2に書きました。

図2
これは覚えて下さい。(導出は教科書等で各自確認して下さい)
そして、これをベクトル法で解いていきます。何を求めるのか?を常に意識して下さい!
今電流条件が与えられたので、V0を求めるのです。
単純にV= IRが使えないから以下のベクトル法で解くのです。
「例)電流がsin型で変化するとき」、
Step1)初期条件sin0=0なので、まず右向きにV- Iが同位相なVrを書きます。
step2)次に図2よりVLは位相が電流に対して電圧がπ/2進んでいるのでVrにπ/2反時計回り進んだ上向きにVLを書きます。
step3)最後に図2よりVCは電流に対して電圧がπ/2遅れているのでマイナスπ/2反時計回りの位置にある、即ち下向きに書きます。
step 4)ベクトルの合成を行い、三平方の定理より合成した大きさ(これがV0の大きさ)とV rとの角度の差φ(φはi0とV0の位相のズレ)をtanで表して合成した位相のずれを確認します。
この4stepを図4に書きました。
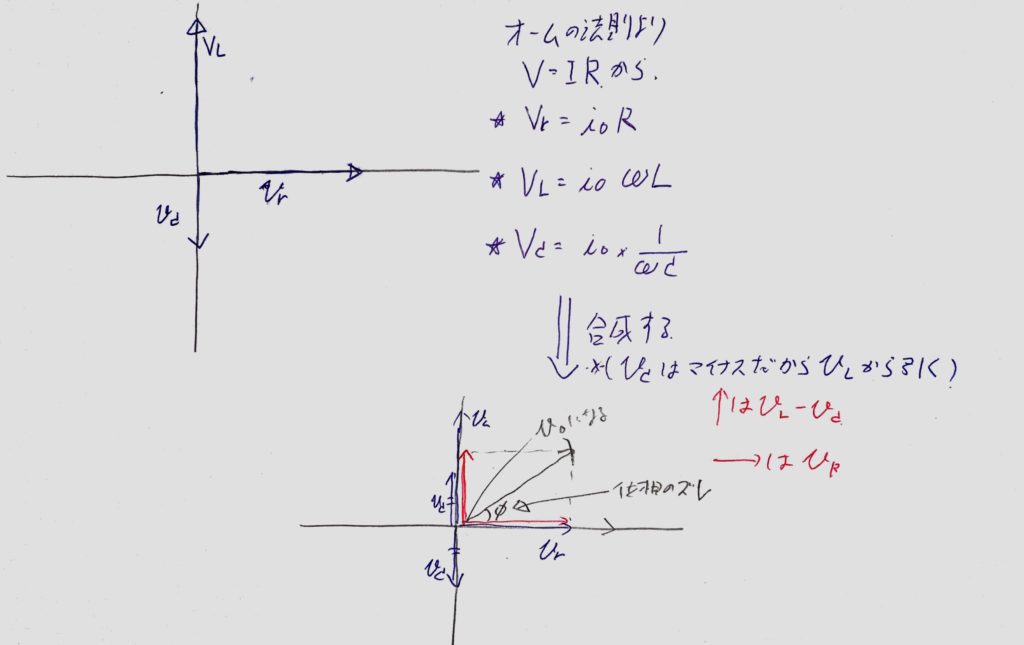
図4
何を求めているのか迷子になっていませんか?
V0でしたね。図4の右下のちょうど右上を向いているベクトルがV0です。大きさは三平方の定理より、
|V0|=√(i0R)^2+{i0(ωL-1/ωC}^2
φはtanで表すこと。
tanφ={ωL-(1/ωC)}/R
この2つが答えです。つまり位相がiよりφ進み大きさは|V0|。
これでベクトル法以上となります。これだけではまだ複雑と思う方が多いと思いますが、(特にtype2の人)実際に問題を解き始めるとこの有り難さが解ってきます!実際にこの範囲の問題をやってみてもらうといいかと思います。
近々、要望があればどこかの入試問題をベクトル法で解く記事をupしようかなと思っています。
今回もご覧いただき有難うございました。お役に立ちましたら、シェア&当サイト公式Twitterのフォロー(Twitterのリンクはこちらから)をお願いします。毎日記事更新情報やお役立ちtipsをtweetしています。
質問・記事について・誤植・その他のお問い合わせはコメント欄までお願い致します。

