
ベクトルの成分表示
この記事では、「ベクトルの向き」を具体的に数字で表す「成分表示」について解説して行きます。
ベクトルの成分表示とは
以前の記事「ベクトルを始めから教えます」の続編として、今回はベクトルの成分表示を紹介します。
さて、ベクトルは「向き」と「大きさ」を持ったものでしたが、
どのくらいの向き(傾き)なのかや、大きさについて”成分表示”の考え方を使う事によって表す事ができます。
また、足し算引き算や掛け算(内積)などでも、成分表示を使った方法で計算する方法があります。
まず以下の<図1>をご覧下さい。
<図1>
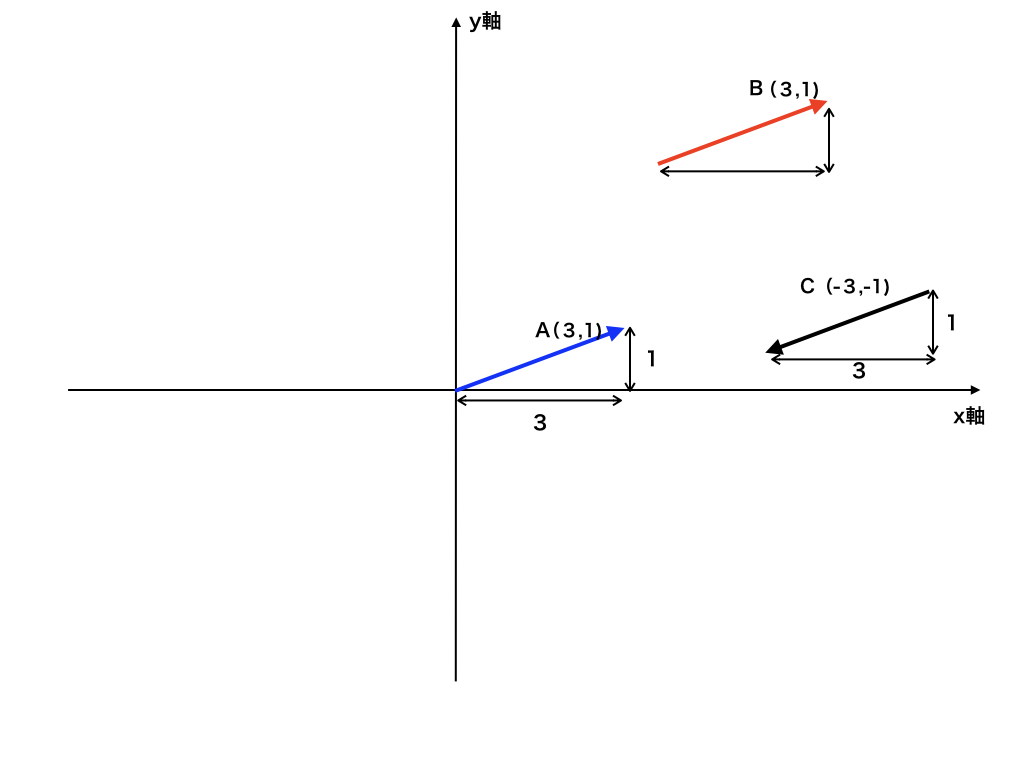
原点Oのxーy座標です。
青色のAベクトルは、始点を原点Oにおいて、(x,y)=(3、1)が終点(矢印の先)のベクトルです。
$$この様なベクトルを\vec {A}=( 3,1) $$
と表す事ができます。これがベクトルの成分表示です。
ただし、普通の座標表示と違う点として、成分表示は、あくまで向き(傾き)を表しているだけなので、
赤色のBベクトルの様に座標上のどこにいても、
同じベクトル(=ベクトルの相等)であれば成分表示も同じ(3,1)になります。
<図1>を一見すると赤色Bベクトルは、始点が(6、4)あたりにあるので、
ベクトルを習いたての人はBベクトルの成分表示を(9,5)などの様にしてしまう事があるので要注意です!
つぎに、赤色のベクトルCに注目してみて下さい。
このベクトルは、向きが逆で大きさが同じベクトル、すなわち「逆ベクトル」です。
逆ベクトルは向きが逆なので、xy成分に両方ー(マイナス)がつきます。
ベクトルの大きさを成分表示で求める
ベクトルの「向き」を成分表示で表したので、
今度はもう一つの「大きさ」も成分表示を使って表してみます。
ベクトルの大きさ=長さは、<三平方の定理>を使って求めます。
$$具体的には、| \vec {A}| =\sqrt {3^{2}+1^{2}}=\sqrt {10}$$
この様に計算できます。
ベクトルの成分表示での足し算と引き算
ベクトルの足し算、引き算はベクトルの終点と始点をつなげ、
はじめのベクトルの始点からつなげたベクトルの終点までのベクトルで表すことが出来ました。
<図2>をご覧下さい。
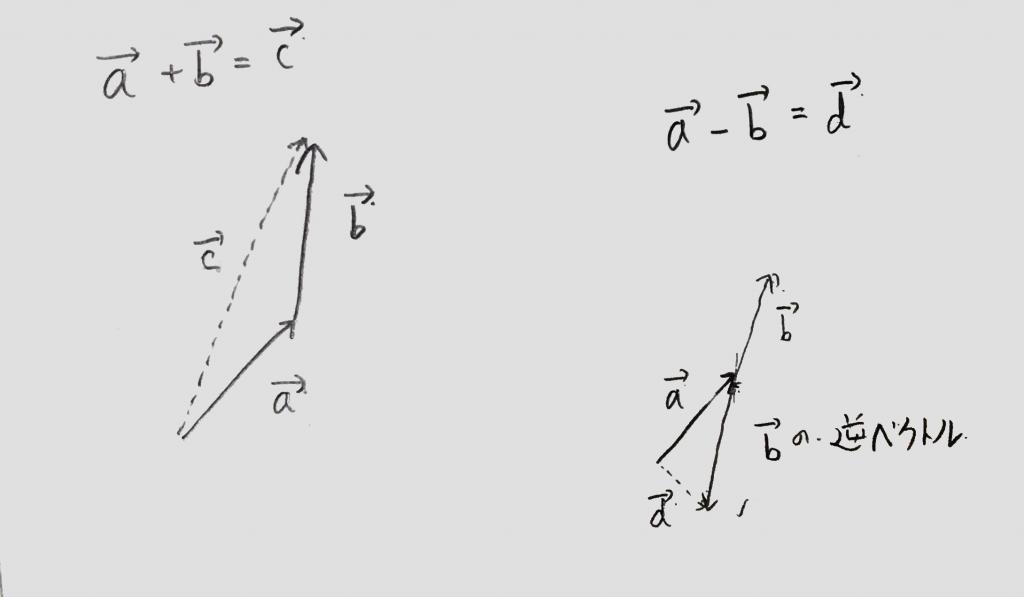
<図2>
これを、成分表示で計算するには、
aベクトルの成分表示を仮に、$$\vec {a}=( a_{x},a_{y}) とします。$$
さらにbベクトルの成分表示を仮に、$$\vec {a}=( b_{x},b_{y}) とします。$$
$$これらを\vec {a}+\vec {b}=( a_{x}+b_{x},a_{y}+b_{y})や$$
$$\overrightarrow {a}-\overrightarrow {b}=( a_{x}-b_{x},a_{y}-b_{y})の様に$$
同じ成分で足し引きするだけです。
ベクトルの内積(成分表示編)
ここからはベクトルの掛け算(内積)を成分表示で計算する方法を解説して行きます。
ベクトルの掛け算については、下の記事で詳しく説明しているので
未習/苦手な方はそちらを先に読んでみて下さい。
>>先に「ベクトルの内積がわかる!ベクトル同士の掛け算の正体」を読む
さて、ベクトルの内積は、<図3>の様に

<図3:ベクトルの内積>
$$\vec {a}\cdot \vec {b}=| \vec {a}|| \vec {b}| \cos \theta $$
で表されましたが、成分表示での内積の計算はもっとシンプルです。
$$\overrightarrow {a}=( a_{x},a_{y}) ,\overrightarrow {b}=(b_{x},b_{y})とする時 $$
$$\overrightarrow {a}\cdot \overrightarrow {b}=a_{x}b_{x}+a_{y}b_{y}$$
この様に、成分表示で表されたベクトルの内積は、(x成分同士を掛けた数+y成分同士を掛けた数)になります。
ベクトルの一次独立へ
ベクトルの成分表示のあらましと、計算の仕方が理解出来たら、「ベクトルの一次独立」に進みましょう。
※ベクトルの他の分野は「ベクトルとは?0から始める解説記事9選」にまとめています。
その定義を理解する為に、成分表示がわかっていると重宝します。
次の記事「ベクトルの一次独立って何?」を読む。
まとめ
この記事では、これまで図を描いて示すしかなかったベクトルを、
(x、y)の数で表す方法と、その成分表示を使ったベクトルの計算を紹介しました。
どちらかだけ使えれば良いという訳ではなく、
両方の関係を図で理解して自由に両方を使いこなせる様になりましょう。
今回も最後までご覧いただき有難うございました。
質問・記事について・誤植・その他のお問い合わせはコメント欄までお願い致します!
お役に立ちましたら、シェア&当サイト公式Twitter(@linkyjuku_tweet)のフォローをお願いします!

