
点が移動するタイプの確率漸化式
今回は、確率漸化式の中でも「移動型」(正式名称ではありません。念のため)を扱います。
問題集などを開くとこのタイプは非常によく出題されている事が分かると思います。
例えば、座標上の
・x軸上を移動する型
・xy平面を移動する型
や、
・立体図形の頂点を移動する型
などなど。
これらのタイプは、色々な問題を解いておく価値があります。
確率漸化式とは?という人は→「良問で学ぶ確率漸化式の解き方\数列と確率の融合」を先にご覧下さい。
目次(タップした所へ飛びます)
点が平面や立体を動くタイプの確率漸化式
早速「立体図形の各頂点を移動する型」の実例を通して解法を身に付けておきましょう。
今回選んだ問題は正四面体なので、立体型でも比較的簡単な方です。
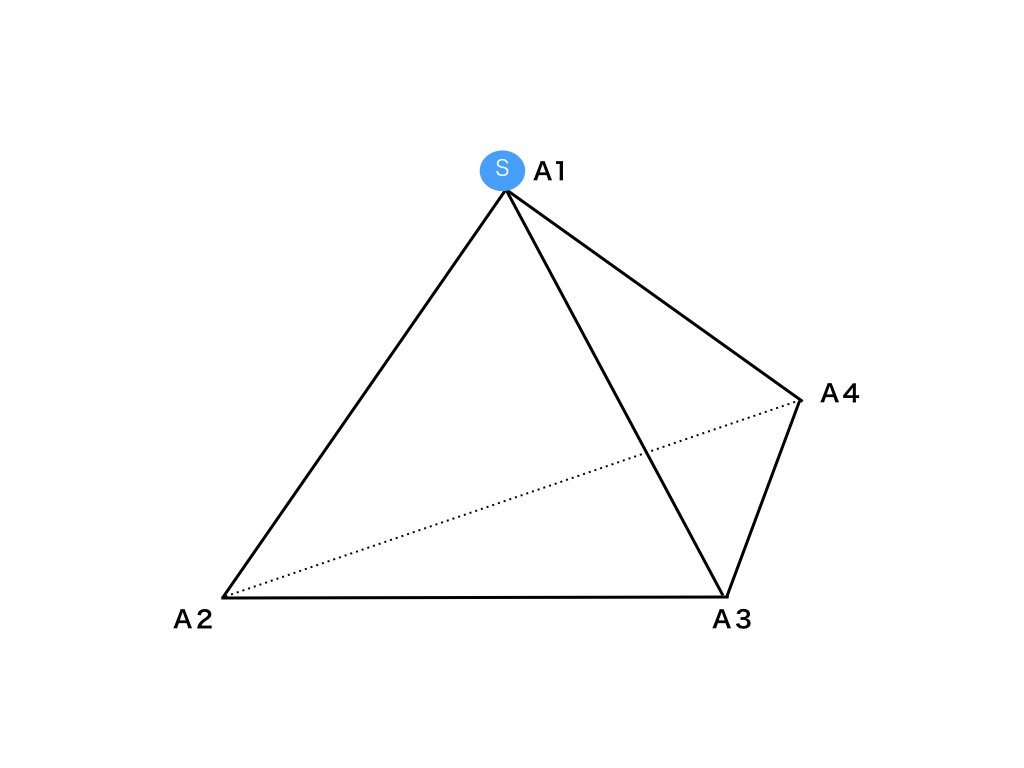
問:正四面体の頂点を移動する点とサイコロの問題
問題:正四面体が有り、その各頂点を、A1,A2,A3,A4とする。
ここで、1〜6までの目があるサイコロを振り、出た目の値をmとする。
今、動点SがAkにあり、サイコロを振って出た目mが【5,6,k】のいずれかであればAkにとどまり、
それ以外の目が出た時はAmへと移動する。
最初に動点SはA1にあり、n回サイコロを投げた時に点SがA1にある確率を”Pn”とするとき、
以下の問いに答えよ。
(1)P2を求めよ。
(2)P(n+1)とPnの関係式(漸化式)を作れ
(3)Pnをnの式で表せ。(問2で作った漸化式を解いて、一般項Pnを求めよ)
(4)nを無限回行った時のPnの値を求めよ。(問4のみ極限を利用するので理系向けです。)
解答1:先に第1回目を求める「重複なく、そしてモレなく」
解答解説:問1:まずは、P1をもとめてみます。
はじめに動点SがA1にいることから、
その点から動かなければ良いので、サイコロの目が1、5、6のいずれかが
出る確率を求めると$$\frac{3}{6}=\frac{1}{2}$$
つぎに、問題のP2、すなわち二回サイコロを振ったのちに、
動点SがA1にいる場合は2通り考えられます。
・一つは、1回目で1、5、6の目が出て、2回目も1、5、6の目が出る=「一度も動かないパターン」
$$より、(一):\frac{3}{6} × \frac{3}{6} =\frac{1}{4}$$
(注意)二つ目は、(たまにこの様なミスをする人がいます。)
「2回目で1が出れば1回目のサイコロは何が出てもいい」ので
$$\frac{6}{6} × \frac{1}{6}」としてしまうとアウトです。$$
場合の数と確率の基本はいかに“重複なく、そしてモレなく”計算できるかです。
極論ですが、どんな難問でもこの基本に従って数え上げれば必ず正解出来るのです。
では、この2つ目のどこが“重複なく、そしてモレなく”に反しているのでしょう?
すぐに気づいた人も多いでしょう。
「1投目のところで(一)の1、5、6で数えている部分を重複して計算してしまっているのです」
よって、(二)は一回目で1、5、6以外の目が出て、二回目で1の目が出るパターン、が正しいのです。
ゆえに、
$$(二):\frac{1}{2} × \frac{1}{6}=\frac{1}{12}$$
$$(一)と(二)を足して、\frac{1}{4}+\frac{1}{12}=\frac{1}{3}$$
“重複なく、そしてモレなく”要注意です。
解答2:n回目とn+1回目の推移図を作る
解説問2:n回目とn+1回目の推移図を書いて漸化式を作ります。→<推移図>
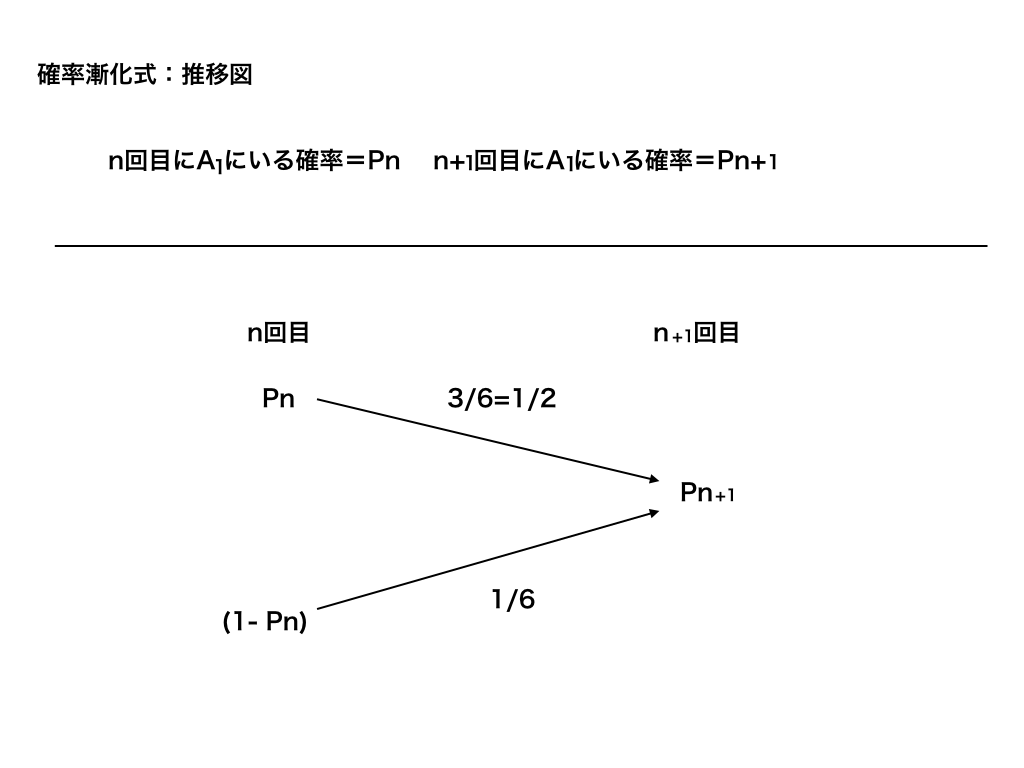
<n回目とn+1回目の推移図>
n回目にA1にいる確率はPn、そうでない場合はにいるので
A2,A3,A4(余事象の確率)、(1-Pn)
$$n+1回目にA_{1}にいる為にはPn× \frac{3}{6}$$
(サイコロの目が1or5or6)と・・・(1)
$$(1-Pn)× \frac{1}{6}$$
(サイコロの目が1)で有ればいいので・・・(2)
$$(1)+(2)より、P_{n+1}=Pn× \frac{1}{3}+(1-Pn)× \frac{1}{6}$$
$$P_{n+1}=\frac{Pn}{3}+\frac{1}{6}$$
解説問3:この漸化式は「等比数列帰着型」です。
漸化式の解き方は→「漸化式第2回:等比数列帰着型の漸化式の解き方」で紹介した一般項の求め方を使って解いていきます。
特性方程式を利用して、
$$P_{n+1}=α、P_{n}=αとしてα=\frac{α}{3}+\frac{1}{6}$$
$$\frac{2}{3}α=\frac{1}{6}よって、α=\frac{1}{4}$$
$$(P_{n+1}-\frac{1}{4})=\frac{1}{3}(P_{n}-\frac{1}{4})$$
ここで一旦Qnの数列に置き換えて計算していきます。
$$P_{1}=\frac{1}{2}より(P_{n}-\frac{1}{4})=Q_{n}とすると$$
$$Q_{n+1}=\frac{1}{3}Q_{n}$$
$$Q_{1}=\frac{1}{4}$$
$$Q_{n}=\frac{1}{4}×( \frac{1}{3})^{n-1}$$
Qnが解けたので、Pnの数列に戻します。
$$P_{n}-\frac{1}{4}=\frac{1}{4}× (\frac{1}{3})^{n-1}$$
これを整理して、
$$以上より、P_{n}=\frac{1}{4}+\frac{1}{4}× (\frac{1}{3})^{n-1}$$
解説問4 :確率漸化式の極限(数学Ⅲ:理系向け)
$$\lim _{n→∞ }P_{n} を求めるだけです。$$
極限計算のキソ知識が必要なので、未習の人は→「極限を0から徹底解説した6記事」の最初の記事を読んでおいて下さい。
$$\lim _{n→∞ } (\frac{1}{4}+\frac{1}{4}× (\frac{1}{3})^{n-1})を求めます。$$
$$n→∞の時(\frac{1}{3})^{n-1}→0$$
$$よって、P_{n}は\frac{1}{4}に収束します。$$
従ってサイコロを振り続けると、
$$A_{1}にいる確率は\frac{1}{4}に収束する。と言えます。$$
移動型の確率漸化式と関連記事まとめ
これまでも書いてきたのですが、確率漸化式は「場合の数と確率」分野と、
「数列、特に漸化式の解き方」の両方を復習できる非常に効率的な分野です。
難関文系・理系頻出分野でもあるので、定期的に問題を復習しておきましょう。
<おススメ記事3選>
「確率漸化式の応用編:連立漸化式を解くタイプの問題」を読む。
「数列の漸化式の解き方全12パターン完全網羅」を読む。
「場合の数と確率の解説記事まとめ」を読む。
今回もご覧いただき有難うございました。
お役に立ちましたら、snsでシェア&当サイト公式Twitterのフォローをお願いします!
質問・記事について・誤植・その他のお問い合わせはコメント欄orTwitterまでお願い致します

